3.2w+
社区成员
- 主页
- 问答
求一个递推公式 （hook formula）
这里高人很多，小弟向大家请教一个递推公式是如何得来的！
题目背景是这样的：n^2个不同高度的人前后排成n排n列，每排n人，要求每列后面的比前面高，每排左边的比右边的高，问总共能有多少满足要求的种排法。
问题更一般的情形是在正整数n的所有拆分的Ferrers图的n个格里填上1～n之间的数，满足每行从左到右递增，每列从下到上递增。求n的满足要求的填充方案数F(n）。
比如一个3的满足要求的填充方案有： 1 2 3 2 3
1 3 1 2
已知F（n）满足递推公式：F(n)=F(n-1)+(n-1)*F(n-2)
这个问题叫做hook formula, F(n）有一个公式可求，但关于它的证明大都有好几页，而且都是英文。小弟希望大家讨论讨论这个公式是怎么推出来的。小弟先谢过大家了！
题目背景是这样的：n^2个不同高度的人前后排成n排n列，每排n人，要求每列后面的比前面高，每排左边的比右边的高，问总共能有多少满足要求的种排法。
问题更一般的情形是在正整数n的所有拆分的Ferrers图的n个格里填上1～n之间的数，满足每行从左到右递增，每列从下到上递增。求n的满足要求的填充方案数F(n）。
比如一个3的满足要求的填充方案有： 1 2 3 2 3
1 3 1 2
已知F（n）满足递推公式：F(n)=F(n-1)+(n-1)*F(n-2)
这个问题叫做hook formula, F(n）有一个公式可求，但关于它的证明大都有好几页，而且都是英文。小弟希望大家讨论讨论这个公式是怎么推出来的。小弟先谢过大家了！
...全文
请发表友善的回复…
发表回复
wesweeky 2011-05-23
牛逼 最近研究整数分划用到这个 看看。 牛人很多
linren 2009-08-24
[Quote=引用 39 楼 linren 的回复:]
只用证明杨氏图表与对合之间存在一一对应的关系就可以了……
[/Quote]
这一步的证明有着重要的意义……
把复杂的整数分拆和HOOK FORMULA的细节全部都屏蔽掉（注意：HOOK FORMULA中的函数hλ((x,y))非初等函数，所以说这一步证明的意义非常重大）……
把问题转换成为了一种更加简单的问题==》求对合数
只用证明杨氏图表与对合之间存在一一对应的关系就可以了……
[/Quote]
这一步的证明有着重要的意义……
把复杂的整数分拆和HOOK FORMULA的细节全部都屏蔽掉（注意：HOOK FORMULA中的函数hλ((x,y))非初等函数，所以说这一步证明的意义非常重大）……
把问题转换成为了一种更加简单的问题==》求对合数
linren 2009-08-24
[Quote=引用 38 楼 new_00006 的回复:]
呵呵！大家想啊，那个递推公式啊！
[/Quote]
证明递推公式：F(n)=F(n-1)+(n-1)F(n-2)
只用证明杨氏图表与对合之间存在一一对应的关系就可以了……
证明的方法就在37楼提供的链接中……
就像高德纳所说“没有非常简单的办法来证明”这个递推公式……
呵呵！大家想啊，那个递推公式啊！
[/Quote]
证明递推公式：F(n)=F(n-1)+(n-1)F(n-2)
只用证明杨氏图表与对合之间存在一一对应的关系就可以了……
证明的方法就在37楼提供的链接中……
就像高德纳所说“没有非常简单的办法来证明”这个递推公式……
new_00006 2009-08-24
呵呵！大家想啊，那个递推公式啊！
linren 2009-08-24
《计算机程序设计艺术（第三卷）》
5.1.4 图表和对合
【摘抄】
1）为了简便起见，把“杨氏图表”简称为“图表”
2）对合和图表之间的这一联系决不是显然的，而且大概也没有非常简单的办法来证明它。我们将要讨论的证明包含一个非常有趣的图标构造算法，它有若干其它意外的性质，该算法是以把新元素插入图表的一个特殊过程为基础的。
【说明】
书中有完美的证明……
这里就不重复书中的证明办法了（因为一些图和符号表示起来比较困难）
下载地址：
part1：http://download.csdn.net/source/1311923
part2：http://download.csdn.net/source/1311947
part3：http://download.csdn.net/source/1311981
part4：http://download.csdn.net/source/1312026
下载完后
将文件名分别改为：
3.part1.rar
3.part2.rar
3.part3.rar
3.part4.rar
就可以进行解压缩了……
5.1.4 图表和对合
【摘抄】
1）为了简便起见，把“杨氏图表”简称为“图表”
2）对合和图表之间的这一联系决不是显然的，而且大概也没有非常简单的办法来证明它。我们将要讨论的证明包含一个非常有趣的图标构造算法，它有若干其它意外的性质，该算法是以把新元素插入图表的一个特殊过程为基础的。
【说明】
书中有完美的证明……
这里就不重复书中的证明办法了（因为一些图和符号表示起来比较困难）
下载地址：
part1：http://download.csdn.net/source/1311923
part2：http://download.csdn.net/source/1311947
part3：http://download.csdn.net/source/1311981
part4：http://download.csdn.net/source/1312026
下载完后
将文件名分别改为：
3.part1.rar
3.part2.rar
3.part3.rar
3.part4.rar
就可以进行解压缩了……
chiwenzi 2009-08-24
《计算机程序设计艺术》好像听说过这本书
linren 2009-08-24
整数拆分与Young tableaux之间有种关系……
叫做Schensted Correspondence
这里有一段资料：
http://mathworld.wolfram.com/SchenstedCorrespondence.html
资料中提到了一本书——《The Art of Computer Programming, Vol. 3: Sorting and Searching, 2nd ed.》
就是《计算机程序设计艺术（第三卷）》
在CSDN上有高清的下载版……
翻了几页发现真的是天书呢……
叫做Schensted Correspondence
这里有一段资料：
http://mathworld.wolfram.com/SchenstedCorrespondence.html
资料中提到了一本书——《The Art of Computer Programming, Vol. 3: Sorting and Searching, 2nd ed.》
就是《计算机程序设计艺术（第三卷）》
在CSDN上有高清的下载版……
翻了几页发现真的是天书呢……
wuchenghao19891 2009-08-24
佩服大家的敬业精神！尊敬！
new_00006 2009-08-24
呵呵，看到了，再等一周结贴，看还有没有别的解答方法。谢谢了，我看的证明是用hook length证明的，而且没看明白。虽然这个证明现在也还没看明白，但比那个要简单多了。而且讲到了递推公式的由来。
linren 2009-08-24
[Quote=引用 42 楼 chenia186 的回复:]
问个问题 每一行（列） 必须要填满？ 能有空缺吗
“
n=3时的合理填充有：
3 | | |
2 | | 2 | 3
1 |1 2 3 | 1 3| 1 2
”
没看太懂
[/Quote]
下面这段话只是帖子的一个引言：
n^2个不同高度的人前后排成n排n列，每排n人，要求每列后面的比前面高，每排左边的比右边的高，问总共能有多少满足要求的种排法。
一开始以为是要把n*n个数放入n*n的矩阵中
后来明白其实是要把n个数放入n*n的矩阵中……
这样那句引言就退化成了后者的一种特殊的情况……
变成了把（n*n）个数放入（n*n）*（n*n）的矩阵中的一种情况
也就是把数都摆放在（n*n）*（n*n）的矩阵的左下角的一个n*n的正方形区域当中……
问个问题 每一行（列） 必须要填满？ 能有空缺吗
“
n=3时的合理填充有：
3 | | |
2 | | 2 | 3
1 |1 2 3 | 1 3| 1 2
”
没看太懂
[/Quote]
下面这段话只是帖子的一个引言：
n^2个不同高度的人前后排成n排n列，每排n人，要求每列后面的比前面高，每排左边的比右边的高，问总共能有多少满足要求的种排法。
一开始以为是要把n*n个数放入n*n的矩阵中
后来明白其实是要把n个数放入n*n的矩阵中……
这样那句引言就退化成了后者的一种特殊的情况……
变成了把（n*n）个数放入（n*n）*（n*n）的矩阵中的一种情况
也就是把数都摆放在（n*n）*（n*n）的矩阵的左下角的一个n*n的正方形区域当中……
wo777778 2009-08-24
学习，中~~~~~~
chenia186 2009-08-24
问个问题 每一行（列） 必须要填满？ 能有空缺吗
“
n=3时的合理填充有：
3 | | |
2 | | 2 | 3
1 |1 2 3 | 1 3| 1 2
”
没看太懂
“
n=3时的合理填充有：
3 | | |
2 | | 2 | 3
1 |1 2 3 | 1 3| 1 2
”
没看太懂
linren 2009-08-24
【关于公式来历的一个推理】
如同21楼所说
当n很小的时候F(n)的结果是非常容易计算出来的……
（但是当n变得稍微比较大的话F(n)的结果就马上变得大的惊人了……
当n=20的时候F(n)的结果就连一个长整形数都无法记录……）
数学家在观察数列F(n)的前面几项时……
偶然间发现它们正好与对合数吻合……
于是就想到了通过证明杨氏图表与对合的关系来证明F(n)=I(n)
后来数学家成功的证明了这点（方法如37楼所示）
于是就有了F(n)=F(n-1)+(n-1)*F(n-2)这个递推公式……
如同21楼所说
当n很小的时候F(n)的结果是非常容易计算出来的……
（但是当n变得稍微比较大的话F(n)的结果就马上变得大的惊人了……
当n=20的时候F(n)的结果就连一个长整形数都无法记录……）
数学家在观察数列F(n)的前面几项时……
偶然间发现它们正好与对合数吻合……
于是就想到了通过证明杨氏图表与对合的关系来证明F(n)=I(n)
后来数学家成功的证明了这点（方法如37楼所示）
于是就有了F(n)=F(n-1)+(n-1)*F(n-2)这个递推公式……
linren 2009-08-23
（上接33楼）
【说明】
如果能够找到一种规律
把下面的结果和33楼中的结果一一对应起来……
那么就能解决这个帖子的问题……
尝试了利用hλ、斜线方向、整数分拆的大小等方法对上述结果进行排序……
但是还是无法做到与33楼的结果一一对应起来……
【说明】
如果能够找到一种规律
把下面的结果和33楼中的结果一一对应起来……
那么就能解决这个帖子的问题……
■□□□ hλ: 1 . . .
■□□□ 2 . . .
■□□□ 3 . . .
■□□□ 4 . . .
No: 1
4 . . .
3 . . .
2 . . .
1 . . .
□□□□ hλ: . . . .
■□□□ 1 . . .
■□□□ 2 . . .
■■□□ 4 1 . .
No: 2
. . . .
4 . . .
3 . . .
1 2 . .
No: 3
. . . .
4 . . .
2 . . .
1 3 . .
No: 4
. . . .
3 . . .
2 . . .
1 4 . .
□□□□ hλ: . . . .
□□□□ . . . .
■■□□ 2 1 . .
■■□□ 3 2 . .
No: 5
. . . .
. . . .
3 4 . .
1 2 . .
No: 6
. . . .
. . . .
2 4 . .
1 3 . .
□□□□ hλ: . . . .
□□□□ . . . .
■□□□ 1 . . .
■■■□ 4 2 1 .
No: 7
. . . .
. . . .
4 . . .
1 2 3 .
No: 8
. . . .
. . . .
3 . . .
1 2 4 .
No: 9
. . . .
. . . .
2 . . .
1 3 4 .
□□□□ hλ: . . . .
□□□□ . . . .
□□□□ . . . .
■■■■ 4 3 2 1
No: 10
. . . .
. . . .
. . . .
1 2 3 4尝试了利用hλ、斜线方向、整数分拆的大小等方法对上述结果进行排序……
但是还是无法做到与33楼的结果一一对应起来……
linren 2009-08-23
【程序】
【运行结果】
【说明】
这个程序可以用来打印对合数……
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int check_invo(int *p,int len){
int i;
int *a,*b;
a=(int*)malloc(sizeof(int)*len);
b=(int*)malloc(sizeof(int)*len);
for(i=0;i<len;i++) a[i]=p[i]+1;
for(i=0;i<len;i++) b[i]=a[a[i]-1];
for(i=0;i<len;i++){
if(b[i]!=i+1){
free(a);free(b);return 0;
}
}
free(a);free(b);
return 1;
}
void per_invo(int len){
int *a,*p,*c;
int i,j,k,flg;
int cc;
if(len<1){
printf("error: len<1\n");return;
}
a=(int*)malloc(sizeof(int)*len);
p=(int*)malloc(sizeof(int)*len);
c=(int*)malloc(sizeof(int)*len);
memset(p,0,sizeof(int)*len);
memset(c,0,sizeof(int)*len);
for(i=0;i<len;i++) a[i]=i+1;
k=0;flg=1;cc=0;
while(flg){
for(p[k]=0;p[k]<len;p[k]++){
for(i=0;i<k;i++){
if(p[i]==p[k]) break;
}
if(i!=k) continue;
c[k]++;
if(k==len-1){
if(check_invo(p,len)){
cc++;
printf("No: %d\t(",cc);
for(i=0;i<len-1;i++) printf("%d, ",a[p[i]]);
printf("%d)\n",a[p[i]]);
}
for(i=len-1,j=1;c[i]==j&&i>=0;i--,j++);
if(j==len+1){
flg=0;break;
}
k=i;
if(k<len-1){
memset(c+k+1,0,sizeof(int)*(len-k-1));
}
}
else k++;
}
}
free(p);free(c);free(a);
}
int main(){
per_invo(4);
return 0;
}【运行结果】
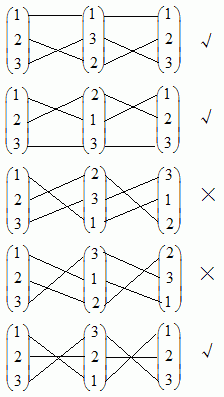
No: 1 (1, 2, 3, 4)
No: 2 (1, 2, 4, 3)
No: 3 (1, 3, 2, 4)
No: 4 (1, 4, 3, 2)
No: 5 (2, 1, 4, 3)
No: 6 (2, 1, 3, 4)
No: 7 (3, 2, 1, 4)
No: 8 (3, 4, 1, 2)
No: 9 (4, 2, 3, 1)
No: 10 (4, 3, 2, 1)
Press any key to continue【说明】
这个程序可以用来打印对合数……
fjtxwd 2009-08-23
强人很多
linren 2009-08-23
求对合数的一种简单方法……
以n=3为例
我们先从集合{1,2,3}的P(3,3)种排列中选择一种作为原序（1,2,3）并且将对合数记为1……
然后使用剩下的P(3,3)-1种情况作为其进行了1次置换后的结果
如果相同的置换进行了2次后得到的结果为原序(1,2,3)
那么对合数就增加1……
整数分解+HOOK FORMULA的效果等同于求对合数……
这一点还是不清楚是为什么……
以n=3为例
我们先从集合{1,2,3}的P(3,3)种排列中选择一种作为原序（1,2,3）并且将对合数记为1……
然后使用剩下的P(3,3)-1种情况作为其进行了1次置换后的结果
如果相同的置换进行了2次后得到的结果为原序(1,2,3)
那么对合数就增加1……
整数分解+HOOK FORMULA的效果等同于求对合数……
这一点还是不清楚是为什么……
linren 2009-08-22
查了一下资料发现了F(n)的一些通项公式的表示方法……
正好是对合置换（Permutation Involution）的公式……
这里有对合的一个解释：
http://zh.wikipedia.org/wiki/%E5%B0%8D%E5%90%88
正好是对合置换（Permutation Involution）的公式……
这里有对合的一个解释：
http://zh.wikipedia.org/wiki/%E5%B0%8D%E5%90%88
ShingRay 2009-08-21
对于某种确定形状的不同 Young Tableux 数目，用 TeX 描述就是这样
\frac{n!}{\prod_{x \in S} f(x)}
n 是格子总数
S 是 n 个格子组成的集合
对于某个格子 x，f(x)定义为它 下面的格子数＋右面的格子数＋1
－－－－－－－－－
不知道这个公式的话，用动态规划也可以
第 n 行放置了 a_n 个，保证 a_1 >= a_2 >= a_3 ……
可以用备忘录形式的动态规划实现
\frac{n!}{\prod_{x \in S} f(x)}
n 是格子总数
S 是 n 个格子组成的集合
对于某个格子 x，f(x)定义为它 下面的格子数＋右面的格子数＋1
－－－－－－－－－
不知道这个公式的话，用动态规划也可以
第 n 行放置了 a_n 个，保证 a_1 >= a_2 >= a_3 ……
可以用备忘录形式的动态规划实现
alphaxiang 2009-08-21
呵呵，感谢大家的关注，希望大家发挥想象，想想这个递推公式是怎么来的，公式的证明（hook length formula）网上能找到，大家可以参考参考。