33,029
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享#include <stdio.h>
#include <math.h>
#define A 0.5
int main(){
double x1,x2;
double a,b;
int flg;
x2=1e-10;
a=x2;
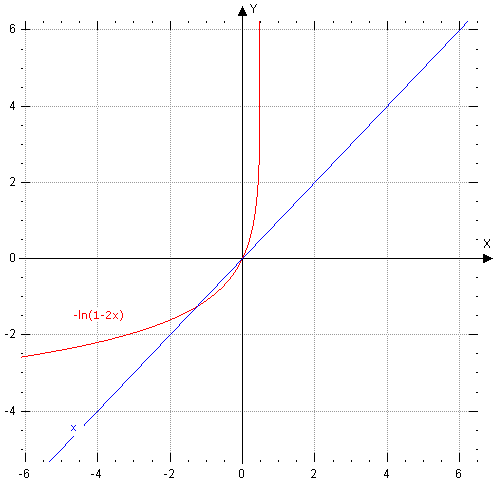
b=-log(1-A*x2);
if(a>b) flg=0;
else flg=1;
while(1){
x2+=1e-5;
a=x2;
b=-log(1-A*x2);
if(flg==0){
if(a<=b) break;
}else{
if(a>b) break;
}
}
while(1){
x1=-log(1-A*x2);
if(x1>x2&&x1-x2<1e-30) break;
else if(x2-x1<1e-30) break;
x2=x1;
}
printf("x = %.10f\n",x1);
return 0;
}
#include <stdio.h>
#include <math.h>
#define A 2.0
int main(){
double x1,x2;
x1=0;x2=-1.0;
while(1){
x1=-log(1-A*x2);
if(x1>x2&&x1-x2<1e-30) break;
else if(x2-x1<1e-30) break;
x2=x1;
}
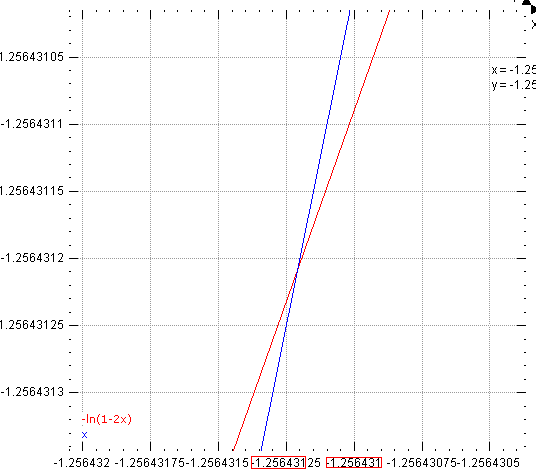
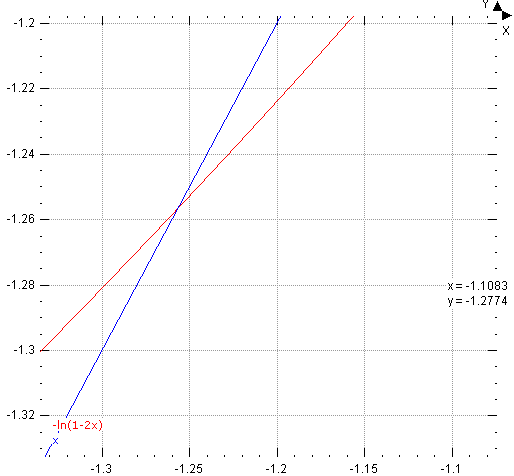
printf("x = %.10f\n",x1);
return 0;
}
#include <stdio.h>
#include <math.h>
#define A 2.0
int main(){
double x1,x2;
x1=0;x2=-2.0;
}
printf("x = %f\n",x1);
return 0;
}

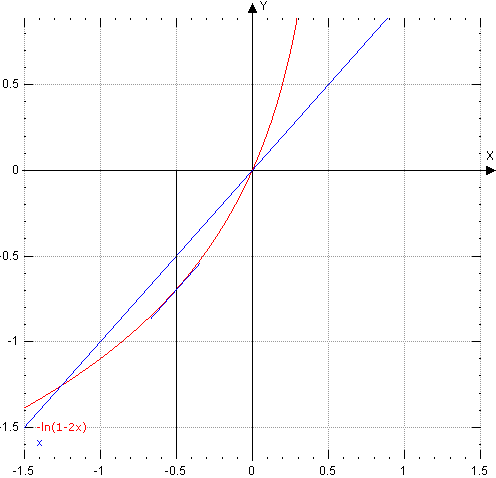
x = -5.1013478342
Press any key to continue