19,472
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享 有没有用代数,方程的方式?
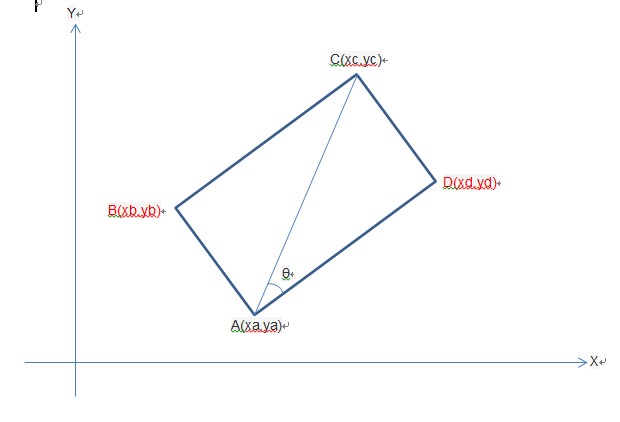
有没有用代数,方程的方式?
POSITION A(0,0);
POSITION C(4,4);
double ANGLE_CAD = 30 * PI/180;
#include <math.h>
const double PI = 3.1415926;
typedef struct POSITION
{
double x;
double y;
public:
POSITION(double xx,double yy)
{
x = xx;
y=yy;
}
} POSITION;
typedef POSITION VECTOR;
//两点之间距离
double distance(POSITION const p1,POSITION const p2)
{
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
//p1指向p2的向量,计算单位向量
void vectorOf(POSITION const p1,POSITION const p2,VECTOR& v)
{
v.x=p2.x-p1.x;
v.y=p2.y-p1.y;
double len = sqrt(v.x*v.x+v.y*v.y);
if(len>0.0000001)
{
v.x = v.x/len;
v.y = v.y/len;
}
}
//向量v0转到angle得到v
void rotate(VECTOR const v0,VECTOR& v,double angle)
{
double cost = cos(angle);
double sint = sin(angle);
v.x = v0.x*cost-v0.y*sint;
v.y = v0.x*sint+v0.y*cost;
}
//p0沿v向移动len的p1
void movePosition(POSITION const p0,VECTOR const v,double len,POSITION & p1)
{
p1.x = p0.x +v.x*len;
p1.y = p0.y +v.y*len;
}
int main(int argc, char* argv[])
{
POSITION A(0,0);
POSITION C(4,4);
double ANGLE_CAD = 30 * PI/180;
double AC = distance(A,C);
double AD = AC*cos(ANGLE_CAD);
double AB = AC*sin(ANGLE_CAD);
VECTOR V_AC(0,0);
vectorOf(A,C,V_AC);
//求D
VECTOR V_AD(0,0);
rotate(V_AC,V_AD,-ANGLE_CAD);
POSITION D(0,0);
movePosition(A,V_AD,AD,D);
//求B
VECTOR V_AB(0,0);
rotate(V_AC,V_AB,PI/2-ANGLE_CAD);
POSITION B(0,0);
movePosition(A,V_AB,AB,B);
return 0;
}