64,636
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享/**
*judge if linear equations has positive integer solutions
*vs 2012
*c++11
*/
#include <iostream>
using namespace std;
int main()
{
//TODO :以下未考虑除数为0
double a=0,b=0,c=0;
cout<<"Enter a,b,c:"<<endl;
cin>>a>>b>>c;
bool swapped=a>b;
if(swapped)swap(a,b);
double u,v;
u=c/a;
v=b/a;
double uf=u-static_cast<int>(u);
double vf=v-static_cast<int>(v);
const double epsilon=(numeric_limits<double>::epsilon());
int upb=static_cast<int>(c/b);
int less=-1;
for (int i = 1; i <= upb; i++)
{
double x=u-v*i;
double xx=floor(x+.5);
if(fabs(x-xx)<=epsilon)
{
if(swapped)
cout<<"A sultion : "<<i<<" , "<<static_cast<int>(x)<<endl;
else
cout<<"A sultion : "<<static_cast<int>(x)<<" , "<<i<<endl;
break;
}
}
system("pause");
}
#include<iostream>
#include <cstring>
typedef long long lint;
lint ex_gcd(lint a, lint b, lint& x, lint& y)
{
if(b == 0)
{
x = 1;
y = 0;
return a;
}
lint r = ex_gcd(b, a % b, x, y);
lint t = x;
x = y;
y = t - a / b * y;
return r;
}
bool check(lint a, lint b, lint c, lint& x, lint& y)
{
lint r = ex_gcd(a, b, x, y);
if(c % r)
{
return false;
}
a /= r; b /= r; c /= r;
x *= c;
x = ((x % b) + b ) % b;
y = (c - a * x) / b;
return y >= 0;
}
int main()
{
lint a = 3000000000000L;
lint b = 5000000000000L;
lint c = 8000000000000L;
lint x, y;
if(check(a, b, c, x, y))
{
printf("其中一组解是:\n x = %lld, y = %lld\n", x, y);
}
else
{
printf("无解\n");
}
return 0;
}
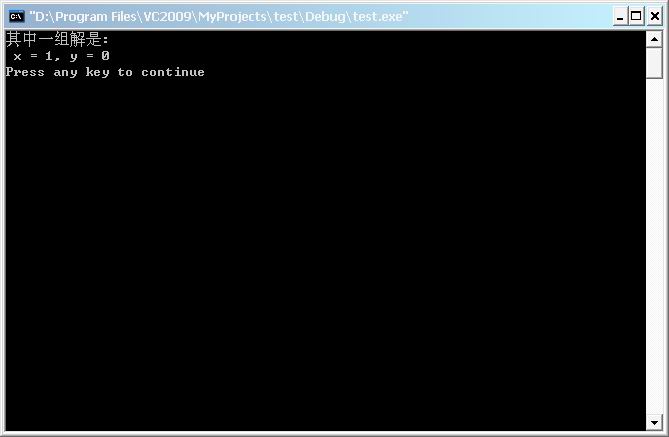 [/quote][/quote]
[/quote][/quote]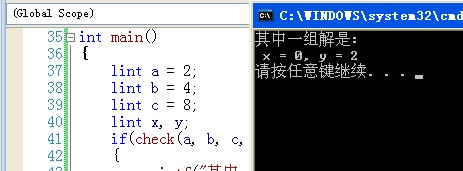
 [/quote]
[/quote]
 你这个不还是枚举[/quote]
这个不是枚举。如果a,b不等于0,那么,与x轴的交点是(c/a,0),如果c/a小于1那么没正整数解,因为横轴(0,c/a)之间没有正整数了;如果c/a >= 1满足,而直线与y轴的交点是(0,c/b),如果c/b<1,那么没有正整数解,反之c/b>=1 并且c/a >= 1,则有正整数解。你问得不是有没有正整数解么?if就判断出来了,也能叫枚举?[/quote]
数学证明里证明某个命题为假有种常用的方法叫举反例,下面就是我提出的反例
a=2; b=3;
c=4;
c/a>1; c/b>1
2x+3y=4
你给我找个正整数解试试。其实压根不需要找什么反例,从你的条件c/b>=1 并且c/a >= 1(相当于c>=b c>=a)就能轻易看出你的命题何等地不靠谱[/quote]额,不好意思,考虑还是太浅显了
你这个不还是枚举[/quote]
这个不是枚举。如果a,b不等于0,那么,与x轴的交点是(c/a,0),如果c/a小于1那么没正整数解,因为横轴(0,c/a)之间没有正整数了;如果c/a >= 1满足,而直线与y轴的交点是(0,c/b),如果c/b<1,那么没有正整数解,反之c/b>=1 并且c/a >= 1,则有正整数解。你问得不是有没有正整数解么?if就判断出来了,也能叫枚举?[/quote]
数学证明里证明某个命题为假有种常用的方法叫举反例,下面就是我提出的反例
a=2; b=3;
c=4;
c/a>1; c/b>1
2x+3y=4
你给我找个正整数解试试。其实压根不需要找什么反例,从你的条件c/b>=1 并且c/a >= 1(相当于c>=b c>=a)就能轻易看出你的命题何等地不靠谱[/quote]额,不好意思,考虑还是太浅显了 你这个不还是枚举[/quote]
这个不是枚举。如果a,b不等于0,那么,与x轴的交点是(c/a,0),如果c/a小于1那么没正整数解,因为横轴(0,c/a)之间没有正整数了;如果c/a >= 1满足,而直线与y轴的交点是(0,c/b),如果c/b<1,那么没有正整数解,反之c/b>=1 并且c/a >= 1,则有正整数解。你问得不是有没有正整数解么?if就判断出来了,也能叫枚举?[/quote]
数学证明里证明某个命题为假有种常用的方法叫举反例,下面就是我提出的反例
a=2; b=3;
c=4;
c/a>1; c/b>1
2x+3y=4
你给我找个正整数解试试。其实压根不需要找什么反例,从你的条件c/b>=1 并且c/a >= 1(相当于c>=b c>=a)就能轻易看出你的命题何等地不靠谱
你这个不还是枚举[/quote]
这个不是枚举。如果a,b不等于0,那么,与x轴的交点是(c/a,0),如果c/a小于1那么没正整数解,因为横轴(0,c/a)之间没有正整数了;如果c/a >= 1满足,而直线与y轴的交点是(0,c/b),如果c/b<1,那么没有正整数解,反之c/b>=1 并且c/a >= 1,则有正整数解。你问得不是有没有正整数解么?if就判断出来了,也能叫枚举?[/quote]
数学证明里证明某个命题为假有种常用的方法叫举反例,下面就是我提出的反例
a=2; b=3;
c=4;
c/a>1; c/b>1
2x+3y=4
你给我找个正整数解试试。其实压根不需要找什么反例,从你的条件c/b>=1 并且c/a >= 1(相当于c>=b c>=a)就能轻易看出你的命题何等地不靠谱 你这个不还是枚举[/quote]
这个不是枚举。如果a,b不等于0,那么,与x轴的交点是(c/a,0),如果c/a小于1那么没正整数解,因为横轴(0,c/a)之间没有正整数了;如果c/a >= 1满足,而直线与y轴的交点是(0,c/b),如果c/b<1,那么没有正整数解,反之c/b>=1 并且c/a >= 1,则有正整数解。你问得不是有没有正整数解么?if就判断出来了,也能叫枚举?
你这个不还是枚举[/quote]
这个不是枚举。如果a,b不等于0,那么,与x轴的交点是(c/a,0),如果c/a小于1那么没正整数解,因为横轴(0,c/a)之间没有正整数了;如果c/a >= 1满足,而直线与y轴的交点是(0,c/b),如果c/b<1,那么没有正整数解,反之c/b>=1 并且c/a >= 1,则有正整数解。你问得不是有没有正整数解么?if就判断出来了,也能叫枚举?