51,412
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享






using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace bagItemsTest
{
class Program
{
static void Main(string[] args)
{
int[] a = { 55000, 55000, 63500, 96120, 97000, 102350, 102350, 132510, 135370, 140000, 144000, 166800, 167530, 169800, 178300, 178300, 178800, 179300, 181000, 181000, 181000, 181000, 181000, 181000, 181000, 182200, 183500, 185684, 188800, 188800, 189800, 190800, 190800, 190800, 195684, 198000, 199626, 199626, 199800, 199800, 199900, 201000, 208700, 209800, 209800, 209800, 209800, 209800, 219000, 219000, 219000, 219000, 219800, 220000, 220000, 220000, 220130, 225600, 228000, 228000, 229434, 229800, 229800, 229800, 229800, 235000, 238800, 240000, 240900, 244800, 247800, 248000, 249800, 249800, 249800, 249800, 249800, 249800, 249800, 249800, 250000, 250000, 250000, 250000, 257000, 260800, 279800, 279800, 279800, 279800, 280340, 285000, 295000, 295000, 295000, 298000, 299000, 300000, 300000, 300000, 313701, 328897, 337300, 345000, 350000, 350000, 350000, 350064, 350064, 350064, 350064, 350064, 429800, 430290, 440154, 472200, 472200, 487305, 500500, 506300, 512226, 544110, 749000, 820000, 1100000 };
List<int> ar = a.ToList<int>();
List<int> r = getRresult(ar, 21, 6531127);
}
static Dictionary<int, List<int>> cache = new Dictionary<int, List<int>>();
static long n = 0;
static int m = 0;
//在ar里返回count个数字,使其结果相加=sum
private static List<int> getRresult(List<int> ar, int count, int sum)
{
n++;
if (ar.Count <= 0 || count <= 0 || sum < 55000 || ar.Count < count || sum < count * 55000)
{
return null;
}
int key = (ar.Count.ToString() + count.ToString() + sum.ToString()).GetHashCode();
if (cache.ContainsKey(key))
{
m++;
return cache[key];
}
if (ar.Count == 1 && ar[0] != sum)//只有一个并且不等和
{
return null;
}
if (ar.Count == 1 && ar[0] == sum)
{
return ar;
}
//判断最后一个数字加还是不加入
int i = ar[ar.Count - 1];
List<int> nar2 = new List<int>();
nar2.AddRange(ar);
nar2.Remove(i);//除去最后一个数字
int ncount = count - 1;
int nsum = sum - i;
if (nar2.Count <= 0 || ncount <= 0 || nsum < 55000 || nar2.Count < ncount || sum < count * 55000)//没有了就返回0以结束递归
{
List<int> nar4 = new List<int>();
nar4.AddRange(ar);
nar4.Remove(i);//加入这一个不行,则移除
return getRresult(nar4, count, sum);
}
List<int> nar3 = getRresult(nar2, ncount, nsum);
key = (nar2.Count.ToString() + ncount.ToString() + nsum.ToString()).GetHashCode();
if (!cache.ContainsKey(key))
{
cache.Add(key, nar3);
}
if (nar3 == null)
{
List<int> nar4 = new List<int>();
nar4.AddRange(ar);
nar4.Remove(i);//加入这一个不行,则移除
return getRresult(nar4, count, sum);
}
else
nar3.Add(i);
if (nar3.Count != count)//结果等于但个数不等于
{
List<int> nar4 = new List<int>();
nar4.AddRange(ar);
nar4.Remove(i);//加入这一个不行,则移除
return getRresult(nar4, count, sum);
}
return nar3;
}
}
}
#include <iostream>
#include <functional>
#include <algorithm>
#define SIZE 125
#define MAX 6531127
using namespace std;
static int input[SIZE] = { 55000, 55000, 63500, 96120, 97000,
102350, 102350, 132510, 135370, 140000,
144000, 166800, 167530, 169800, 178300,
178300, 178800, 179300, 181000, 181000,
181000, 181000, 181000, 181000, 181000,
182200, 183500, 185684, 188800, 188800,
189800, 190800, 190800, 190800, 195684,
198000, 199626, 199626, 199800, 199800,
199900, 201000, 208700, 209800, 209800,
209800, 209800, 209800, 219000, 219000,
219000, 219000, 219800, 220000, 220000,
220000, 220130, 225600, 228000, 228000,
229434, 229800, 229800, 229800, 229800,
235000, 238800, 240000, 240900, 244800,
247800, 248000, 249800, 249800, 249800,
249800, 249800, 249800, 249800, 249800,
250000, 250000, 250000, 250000, 257000,
260800, 279800, 279800, 279800, 279800,
280340, 285000, 295000, 295000, 295000,
298000, 299000, 300000, 300000, 300000,
313701, 328897, 337300, 345000, 350000,
350000, 350000, 350064, 350064, 350064,
350064, 350064, 429800, 430290, 440154,
472200, 472200, 487305, 500500, 506300,
512226, 544110, 749000, 820000, 1100000 }, goal_select = 21;
static struct _set
{
char _num_sum[5], _select[5][21];
int rep;
}bag1[MAX + 1], bag2[MAX + 1], *tmp, *dp1, *dp2;
void Print_Select(struct _set *goal,const int rep)
{
int pos_stop = goal[MAX]._num_sum[rep];
cout << "The items are :" << endl;
for (int i = 0; i < pos_stop; i++)
cout << goal[MAX]._select[rep][i] + 1 << ": " << input[goal[MAX]._select[rep][i]] << endl;
}
void Copy(const int m1, const int m2)
{
memcpy(dp2[m2]._num_sum, dp1[m1]._num_sum, sizeof(dp2[m2]._num_sum));
memcpy(dp2[m2]._select, dp1[m1]._select, sizeof(dp2[m2]._select));
dp2[m2].rep = dp1[m1].rep;
}
int Max(const int x, const int y)
{
return x > y ? x : y;
}
void Merge_Bound(struct _set *pos1, struct _set *pos2, struct _set *goal,const int stuff)
{
int ptr_dp1 = 0, ptr_dp2 = 0, tmp_sum, tmp_rep = 0;
int up_bound = Max(pos1->_num_sum[pos1->rep - 1], pos2->_num_sum[pos2->rep - 1]) + 1;
for (int i = 1; i <= up_bound; i++)
{
if (pos1->rep != 0//0代表不合法
&& (pos1->_num_sum)[ptr_dp1] + 1 <= goal_select - 1
&& (pos1->_num_sum)[ptr_dp1] + 1 == i)
{
(goal->_num_sum)[tmp_rep] = tmp_sum = (pos1->_num_sum)[ptr_dp1] + 1;
memcpy((goal->_select)[tmp_rep], (pos1->_select)[ptr_dp1], sizeof((goal->_select)[tmp_rep]));
(goal->_select)[tmp_rep][tmp_sum - 1] = stuff - 1;
ptr_dp1++;
tmp_rep++;
}
else if (pos2->rep != 0
&& (pos2->_num_sum)[ptr_dp2] == i)
{
(goal->_num_sum)[tmp_rep] = (pos2->_num_sum)[ptr_dp2];
memcpy((goal->_select)[tmp_rep], (pos2->_select)[ptr_dp2], sizeof((pos2->_select)[ptr_dp2]));
ptr_dp2++;
tmp_rep++;
}
}
goal->rep = tmp_rep;
}
bool Search(void)
{
int pos, num_sum;
dp1[0].rep = 1;
for (int i = 1; i <= SIZE; i++)
{
dp2[0].rep = 1;
for (int j = 1; j < input[i - 1]; j++)
Copy(j, j);
for (int j = input[i - 1]; j <= MAX; j++)
{
if (j == MAX && dp1[MAX - input[i - 1]]._num_sum[dp1[MAX - input[i - 1]].rep - 1] + 1 == goal_select)//直接输出
{
Copy(MAX - input[i - 1], MAX);
pos = dp1[MAX - input[i - 1]].rep - 1;
dp2[MAX]._num_sum[pos]++;
num_sum = dp2[MAX]._num_sum[pos];
dp2[MAX]._select[pos][num_sum - 1] = i - 1;
Print_Select(dp2, dp2[MAX].rep - 1);
return true;
}
Merge_Bound(&dp1[j - input[i - 1]], &dp1[j], &dp2[j], i);
}
tmp = dp1; dp1 = dp2; dp2 = tmp;
}
return false;
}
int main(void)
{
dp1 = bag1; dp2 = bag2;
memset(dp1, 0, sizeof(dp1));
memset(dp2, 0, sizeof(dp2));
sort(input, input + SIZE);
if (Search())
cout << "SUCCESS" << endl;
else
cout << "FAIL" << endl;
system("pause");
return EXIT_SUCCESS;
}
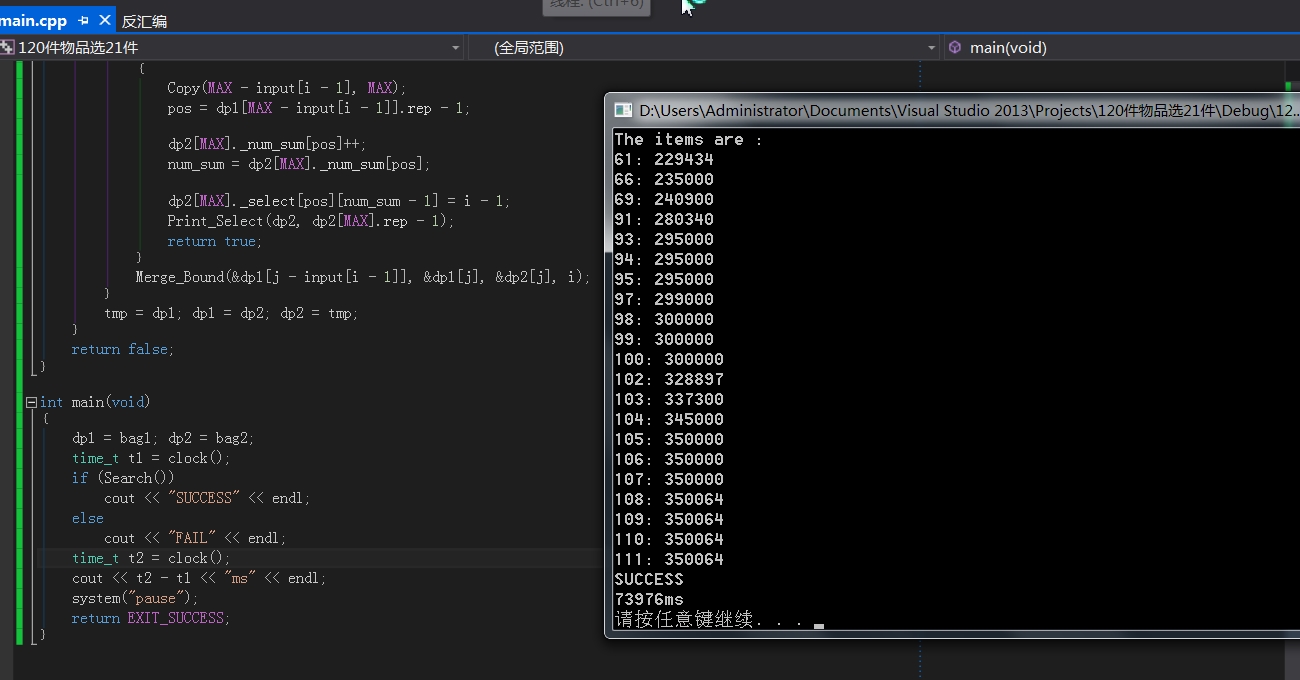 前面那个代码有点错误,会丢包,现在改出来了,通过了例子
考虑到你的找的数字只有21个,因为怕数组溢出我包的容量尽可能缩小了,你想改大的话可以把包的select量拿出来,我就贪方便了直接写结构体里面了
思想就是01背包,这种选物品的问题都是可以转成背包问题解决的,千万不要用枚举,即使是把尾数拆开来算总和的枚举也是一定会溢出的,数据量太大了,而且时间会很慢(指数时间复杂度)
我这个代码时间复杂度是0(C*P*N),(C是选择的元素,P是总和,N是元素个数),空间复杂度是O(C*C*P)
在我的机子跑了79S吧,其实很慢了,因为我的包的总量是按照P来划分的,但是P很大,如果你想快的话可以这样,因为你的数据都是比较大的,可以考虑划分为一个一个segement,比如1W-2W是一个区域,这样把包的容量减少,这样跑起来就快了
如果你的给定数字少的话(比如只有40个),那就直接用超大背包的做法,把数字拆分枚举,再用完全背包,然后合并。[/quote]
腻害呀大神,可惜没有注释看不懂
前面那个代码有点错误,会丢包,现在改出来了,通过了例子
考虑到你的找的数字只有21个,因为怕数组溢出我包的容量尽可能缩小了,你想改大的话可以把包的select量拿出来,我就贪方便了直接写结构体里面了
思想就是01背包,这种选物品的问题都是可以转成背包问题解决的,千万不要用枚举,即使是把尾数拆开来算总和的枚举也是一定会溢出的,数据量太大了,而且时间会很慢(指数时间复杂度)
我这个代码时间复杂度是0(C*P*N),(C是选择的元素,P是总和,N是元素个数),空间复杂度是O(C*C*P)
在我的机子跑了79S吧,其实很慢了,因为我的包的总量是按照P来划分的,但是P很大,如果你想快的话可以这样,因为你的数据都是比较大的,可以考虑划分为一个一个segement,比如1W-2W是一个区域,这样把包的容量减少,这样跑起来就快了
如果你的给定数字少的话(比如只有40个),那就直接用超大背包的做法,把数字拆分枚举,再用完全背包,然后合并。[/quote]
腻害呀大神,可惜没有注释看不懂

#include <iostream>
#include <functional>
#include <algorithm>
#define SIZE 125
#define MAX 6531127
using namespace std;
static int input[SIZE] = { 55000, 55000, 63500, 96120, 97000,
102350, 102350, 132510, 135370, 140000,
144000, 166800, 167530, 169800, 178300,
178300, 178800, 179300, 181000, 181000,
181000, 181000, 181000, 181000, 181000,
182200, 183500, 185684, 188800, 188800,
189800, 190800, 190800, 190800, 195684,
198000, 199626, 199626, 199800, 199800,
199900, 201000, 208700, 209800, 209800,
209800, 209800, 209800, 219000, 219000,
219000, 219000, 219800, 220000, 220000,
220000, 220130, 225600, 228000, 228000,
229434, 229800, 229800, 229800, 229800,
235000, 238800, 240000, 240900, 244800,
247800, 248000, 249800, 249800, 249800,
249800, 249800, 249800, 249800, 249800,
250000, 250000, 250000, 250000, 257000,
260800, 279800, 279800, 279800, 279800,
280340, 285000, 295000, 295000, 295000,
298000, 299000, 300000, 300000, 300000,
313701, 328897, 337300, 345000, 350000,
350000, 350000, 350064, 350064, 350064,
350064, 350064, 429800, 430290, 440154,
472200, 472200, 487305, 500500, 506300,
512226, 544110, 749000, 820000, 1100000 }, goal_select = 21;
static struct _set
{
char _num_sum[5], _select[5][21];
int rep;
}bag1[MAX + 1], bag2[MAX + 1], *tmp, *dp1, *dp2;
void Print_Select(struct _set *goal,const int rep)
{
int pos_stop = goal[MAX]._num_sum[rep];
cout << "The items are :" << endl;
for (int i = 0; i < pos_stop; i++)
cout << goal[MAX]._select[rep][i] + 1 << ": " << input[goal[MAX]._select[rep][i]] << endl;
}
void Copy(const int m1, const int m2)
{
memcpy(dp2[m2]._num_sum, dp1[m1]._num_sum, sizeof(dp2[m2]._num_sum));
memcpy(dp2[m2]._select, dp1[m1]._select, sizeof(dp2[m2]._select));
dp2[m2].rep = dp1[m1].rep;
}
int Max(const int x, const int y)
{
return x > y ? x : y;
}
void Merge_Bound(struct _set *pos1, struct _set *pos2, struct _set *goal,const int stuff)
{
int ptr_dp1 = 0, ptr_dp2 = 0, tmp_sum, tmp_rep = 0;
int up_bound = Max(pos1->_num_sum[pos1->rep - 1], pos2->_num_sum[pos2->rep - 1]) + 1;
for (int i = 1; i <= up_bound; i++)
{
if (pos1->rep != 0//0代表不合法
&& (pos1->_num_sum)[ptr_dp1] + 1 <= goal_select - 1
&& (pos1->_num_sum)[ptr_dp1] + 1 == i)
{
(goal->_num_sum)[tmp_rep] = tmp_sum = (pos1->_num_sum)[ptr_dp1] + 1;
memcpy((goal->_select)[tmp_rep], (pos1->_select)[ptr_dp1], sizeof((goal->_select)[tmp_rep]));
(goal->_select)[tmp_rep][tmp_sum - 1] = stuff - 1;
ptr_dp1++;
tmp_rep++;
}
else if (pos2->rep != 0
&& (pos2->_num_sum)[ptr_dp2] == i)
{
(goal->_num_sum)[tmp_rep] = (pos2->_num_sum)[ptr_dp2];
memcpy((goal->_select)[tmp_rep], (pos2->_select)[ptr_dp2], sizeof((pos2->_select)[ptr_dp2]));
ptr_dp2++;
tmp_rep++;
}
}
goal->rep = tmp_rep;
}
bool Search(void)
{
int pos, num_sum;
dp1[0].rep = 1;
for (int i = 1; i <= SIZE; i++)
{
dp2[0].rep = 1;
for (int j = 1; j < input[i - 1]; j++)
Copy(j, j);
for (int j = input[i - 1]; j <= MAX; j++)
{
if (j == MAX && dp1[MAX - input[i - 1]]._num_sum[dp1[MAX - input[i - 1]].rep - 1] + 1 == goal_select)//直接输出
{
Copy(MAX - input[i - 1], MAX);
pos = dp1[MAX - input[i - 1]].rep - 1;
dp2[MAX]._num_sum[pos]++;
num_sum = dp2[MAX]._num_sum[pos];
dp2[MAX]._select[pos][num_sum - 1] = i - 1;
Print_Select(dp2, dp2[MAX].rep - 1);
return true;
}
Merge_Bound(&dp1[j - input[i - 1]], &dp1[j], &dp2[j], i);
}
tmp = dp1; dp1 = dp2; dp2 = tmp;
}
return false;
}
int main(void)
{
dp1 = bag1; dp2 = bag2;
memset(dp1, 0, sizeof(dp1));
memset(dp2, 0, sizeof(dp2));
sort(input, input + SIZE);
if (Search())
cout << "SUCCESS" << endl;
else
cout << "FAIL" << endl;
system("pause");
return EXIT_SUCCESS;
}
 前面那个代码有点错误,会丢包,现在改出来了,通过了例子
考虑到你的找的数字只有21个,因为怕数组溢出我包的容量尽可能缩小了,你想改大的话可以把包的select量拿出来,我就贪方便了直接写结构体里面了
思想就是01背包,这种选物品的问题都是可以转成背包问题解决的,千万不要用枚举,即使是把尾数拆开来算总和的枚举也是一定会溢出的,数据量太大了,而且时间会很慢(指数时间复杂度)
我这个代码时间复杂度是0(C*P*N),(C是选择的元素,P是总和,N是元素个数),空间复杂度是O(C*C*P)
在我的机子跑了79S吧,其实很慢了,因为我的包的总量是按照P来划分的,但是P很大,如果你想快的话可以这样,因为你的数据都是比较大的,可以考虑划分为一个一个segement,比如1W-2W是一个区域,这样把包的容量减少,这样跑起来就快了
如果你的给定数字少的话(比如只有40个),那就直接用超大背包的做法,把数字拆分枚举,再用完全背包,然后合并。[/quote]
膜拜大神,虽然不是用java写的,但是解决了问题并且给出了解决思路,灰常感激!
前面那个代码有点错误,会丢包,现在改出来了,通过了例子
考虑到你的找的数字只有21个,因为怕数组溢出我包的容量尽可能缩小了,你想改大的话可以把包的select量拿出来,我就贪方便了直接写结构体里面了
思想就是01背包,这种选物品的问题都是可以转成背包问题解决的,千万不要用枚举,即使是把尾数拆开来算总和的枚举也是一定会溢出的,数据量太大了,而且时间会很慢(指数时间复杂度)
我这个代码时间复杂度是0(C*P*N),(C是选择的元素,P是总和,N是元素个数),空间复杂度是O(C*C*P)
在我的机子跑了79S吧,其实很慢了,因为我的包的总量是按照P来划分的,但是P很大,如果你想快的话可以这样,因为你的数据都是比较大的,可以考虑划分为一个一个segement,比如1W-2W是一个区域,这样把包的容量减少,这样跑起来就快了
如果你的给定数字少的话(比如只有40个),那就直接用超大背包的做法,把数字拆分枚举,再用完全背包,然后合并。[/quote]
膜拜大神,虽然不是用java写的,但是解决了问题并且给出了解决思路,灰常感激!
#include <iostream>
#include <functional>
#include <algorithm>
#define SIZE 125
#define MAX 6531127
using namespace std;
static int input[SIZE] = { 55000, 55000, 63500, 96120, 97000,
102350, 102350, 132510, 135370, 140000,
144000, 166800, 167530, 169800, 178300,
178300, 178800, 179300, 181000, 181000,
181000, 181000, 181000, 181000, 181000,
182200, 183500, 185684, 188800, 188800,
189800, 190800, 190800, 190800, 195684,
198000, 199626, 199626, 199800, 199800,
199900, 201000, 208700, 209800, 209800,
209800, 209800, 209800, 219000, 219000,
219000, 219000, 219800, 220000, 220000,
220000, 220130, 225600, 228000, 228000,
229434, 229800, 229800, 229800, 229800,
235000, 238800, 240000, 240900, 244800,
247800, 248000, 249800, 249800, 249800,
249800, 249800, 249800, 249800, 249800,
250000, 250000, 250000, 250000, 257000,
260800, 279800, 279800, 279800, 279800,
280340, 285000, 295000, 295000, 295000,
298000, 299000, 300000, 300000, 300000,
313701, 328897, 337300, 345000, 350000,
350000, 350000, 350064, 350064, 350064,
350064, 350064, 429800, 430290, 440154,
472200, 472200, 487305, 500500, 506300,
512226, 544110, 749000, 820000, 1100000 }, goal_select = 21;
static struct _set
{
char _num_sum[5], _select[5][21];
int rep;
}bag1[MAX + 1], bag2[MAX + 1], *tmp, *dp1, *dp2;
void Print_Select(struct _set *goal,const int rep)
{
int pos_stop = goal[MAX]._num_sum[rep];
cout << "The items are :" << endl;
for (int i = 0; i < pos_stop; i++)
cout << goal[MAX]._select[rep][i] + 1 << ": " << input[goal[MAX]._select[rep][i]] << endl;
}
void Copy(const int m1, const int m2)
{
memcpy(dp2[m2]._num_sum, dp1[m1]._num_sum, sizeof(dp2[m2]._num_sum));
memcpy(dp2[m2]._select, dp1[m1]._select, sizeof(dp2[m2]._select));
dp2[m2].rep = dp1[m1].rep;
}
int Max(const int x, const int y)
{
return x > y ? x : y;
}
void Merge_Bound(struct _set *pos1, struct _set *pos2, struct _set *goal,const int stuff)
{
int ptr_dp1 = 0, ptr_dp2 = 0, tmp_sum, tmp_rep = 0;
int up_bound = Max(pos1->_num_sum[pos1->rep - 1], pos2->_num_sum[pos2->rep - 1]) + 1;
for (int i = 1; i <= up_bound; i++)
{
if (pos1->rep != 0//0代表不合法
&& (pos1->_num_sum)[ptr_dp1] + 1 <= goal_select - 1
&& (pos1->_num_sum)[ptr_dp1] + 1 == i)
{
(goal->_num_sum)[tmp_rep] = tmp_sum = (pos1->_num_sum)[ptr_dp1] + 1;
memcpy((goal->_select)[tmp_rep], (pos1->_select)[ptr_dp1], sizeof((goal->_select)[tmp_rep]));
(goal->_select)[tmp_rep][tmp_sum - 1] = stuff - 1;
ptr_dp1++;
tmp_rep++;
}
else if (pos2->rep != 0
&& (pos2->_num_sum)[ptr_dp2] == i)
{
(goal->_num_sum)[tmp_rep] = (pos2->_num_sum)[ptr_dp2];
memcpy((goal->_select)[tmp_rep], (pos2->_select)[ptr_dp2], sizeof((pos2->_select)[ptr_dp2]));
ptr_dp2++;
tmp_rep++;
}
}
goal->rep = tmp_rep;
}
bool Search(void)
{
int pos, num_sum;
dp1[0].rep = 1;
for (int i = 1; i <= SIZE; i++)
{
dp2[0].rep = 1;
for (int j = 1; j < input[i - 1]; j++)
Copy(j, j);
for (int j = input[i - 1]; j <= MAX; j++)
{
if (j == MAX && dp1[MAX - input[i - 1]]._num_sum[dp1[MAX - input[i - 1]].rep - 1] + 1 == goal_select)//直接输出
{
Copy(MAX - input[i - 1], MAX);
pos = dp1[MAX - input[i - 1]].rep - 1;
dp2[MAX]._num_sum[pos]++;
num_sum = dp2[MAX]._num_sum[pos];
dp2[MAX]._select[pos][num_sum - 1] = i - 1;
Print_Select(dp2, dp2[MAX].rep - 1);
return true;
}
Merge_Bound(&dp1[j - input[i - 1]], &dp1[j], &dp2[j], i);
}
tmp = dp1; dp1 = dp2; dp2 = tmp;
}
return false;
}
int main(void)
{
dp1 = bag1; dp2 = bag2;
memset(dp1, 0, sizeof(dp1));
memset(dp2, 0, sizeof(dp2));
sort(input, input + SIZE);
if (Search())
cout << "SUCCESS" << endl;
else
cout << "FAIL" << endl;
system("pause");
return EXIT_SUCCESS;
}

#include <iostream>
#include <functional>
#include <algorithm>
#define SIZE 10
#define MAX 16
using namespace std;
static int input[SIZE] = { 1,3,5,7,9,11,13,15,17,19 }, goal_select = 2;
static struct _set
{
int _num_sum, _select[10];
}bag[2][MAX + 1], *dp1, *dp2, *tmp;
void Print_Select(struct _set *goal)
{
cout << "The items are !" << endl;
for (int i = 0; i < goal[MAX]._num_sum; i++)
cout << goal[MAX]._select[i] + 1 << ": " << input[goal[MAX]._select[i]] << endl;
}
bool Search(void)
{
int tmp_sum;
dp1 = bag[0], dp2 = bag[1];
bag[0][0]._num_sum = 0;
for (int i = 1; i <= MAX; i++)
dp1[i]._num_sum = -1;
for (int i = 1; i <= SIZE; i++)
{
dp2[0]._num_sum = 0;
for (int j = 1; j < input[i - 1]; j++)
{
dp2[j]._num_sum = tmp_sum = dp1[j]._num_sum;
memcpy(dp2[j]._select, dp1[j]._select, sizeof(dp2[j]._select));
}
for (int j = input[i - 1]; j <= MAX; j++)
{
if (dp1[j - input[i - 1]]._num_sum<goal_select)
{
if (dp1[j - input[i - 1]]._num_sum != -1
&& (dp1[j - input[i - 1]]._num_sum + 1>dp1[j]._num_sum))
{
dp2[j]._num_sum = tmp_sum = dp1[j - input[i - 1]]._num_sum + 1;
memcpy(dp2[j]._select, dp1[j - input[i - 1]]._select, sizeof(dp2[j]._select));
dp2[j]._select[tmp_sum - 1] = i - 1;
}
else
{
dp2[j]._num_sum = tmp_sum = dp1[j]._num_sum;
memcpy(dp2[j]._select, dp1[j]._select, sizeof(dp2[j]._select));
}
}
else if (dp1[j - input[i - 1]]._num_sum >= goal_select)
{
if (dp1[j - input[i - 1]]._num_sum != -1
&& (dp1[j - input[i - 1]]._num_sum + 1< dp1[j]._num_sum))
{
dp2[j]._num_sum = tmp_sum = dp1[j - input[i - 1]]._num_sum + 1;
memcpy(dp2[j]._select, dp1[j - input[i - 1]]._select, sizeof(dp2[j]._select));
dp2[j]._select[tmp_sum - 1] = i - 1;
}
else
{
dp2[j]._num_sum = tmp_sum = dp1[j]._num_sum;
memcpy(dp2[j]._select, dp1[j]._select, sizeof(dp2[j]._select));
}
}
if (dp2[MAX]._num_sum == goal_select)
{
Print_Select(dp2);
return true;
}
}
tmp = dp1; dp1 = dp2; dp2 = tmp;
}
return false;
}
int main(void)
{
memset(bag, 0, sizeof(bag));
sort(input, input + SIZE);
if (Search())
cout << "SUCCESS" << endl;
else
cout << "FAIL" << endl;
system("pause");
return EXIT_SUCCESS;
}