110,986
社区成员
发帖
与我相关
我的任务
分享求C#拟合函数的相关系数R的代码（即线性、多元、指数、对数、幂等拟合）
求C#拟合函数的相关系数R的代码（即线性、多元、指数、对数、幂等拟合）
至于这几个函数的拟合代码，网上已经有了，但是此人没给出相关系数R的计算代码；
有没有人能帮忙写个的？
拟合代码：http://download.csdn.net/detail/flyrp/5250732
至于这几个函数的拟合代码，网上已经有了，但是此人没给出相关系数R的计算代码；
有没有人能帮忙写个的？
拟合代码：http://download.csdn.net/detail/flyrp/5250732
...全文
请发表友善的回复…
发表回复
wanghui0380 2018-01-03
- 打赏
- 举报
额，这个玩意目前的情况是，可以直接使用R语言求解。vs目前可以支持在C#里调用R去玩这类型的项目
xiaoyue月 2018-01-03
- 打赏
- 举报
楼主您好，这个问题最后解决了吗，求出二次拟合的相关系数了吗
fuzhzh345 2017-06-08
- 打赏
- 举报
类2：
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace 高斯消元法
{
class FittingFunct
{
#region 多项式拟合函数,输出系数是y=a0+a1*x+a2*x*x+.........，按a0,a1,a2输出
static public double[] Polyfit(double[] y, double[] x, int order)
{
double[,] guass = Get_Array(y, x, order);
double[] ratio = Cal_Guass(guass, order + 1);
return ratio;
}
#endregion
#region 一次拟合函数，y=a0+a1*x,输出次序是a0,a1
static public double[] Linear(double[] y,double[] x)
{
double[] ratio = Polyfit(y, x, 1);
return ratio;
}
#endregion
#region 一次拟合函数，截距为0，y=a0x,输出次序是a0
static public double[] LinearInterceptZero(double[] y, double[] x)
{
double divisor = 0; //除数
double dividend = 0; //被除数
for (int i = 0; i < x.Length;i++ )
{
divisor += x[i] * x[i];
dividend += x[i] * y[i];
}
if (divisor == 0)
{
throw (new Exception("除数不为0！"));
return null;
}
return new double[] { dividend / divisor };
}
#endregion
#region 二次拟合函数，y=a0+a1*x+a2x²,输出次序是a0,a1,a2
static public double[] TowTimesCurve(double[] y, double[] x)
{
double[] ratio = Polyfit(y, x, 2);
return ratio;
}
#endregion
#region 对数拟合函数,.y= c*(ln x)+b,输出为b,c
static public double[] LOGEST(double[] y, double[] x)
{
double[] lnX = new double[x.Length];
for (int i = 0; i < x.Length; i++)
{
if (x[i] == 0 || x[i] < 0)
{
throw (new Exception("正对非正数取对数！"));
return null;
}
lnX[i] = Math.Log(x[i]);
}
return Linear(y, lnX);
}
#endregion
#region 幂函数拟合模型, y=c*x^b,输出为c,b
static public double[] PowEST(double[] y, double[] x)
{
double[] lnX = new double[x.Length];
double[] lnY = new double[y.Length];
double[] dlinestRet;
for (int i = 0; i < x.Length; i++)
{
lnX[i] = Math.Log(x[i]);
lnY[i] = Math.Log(y[i]);
}
dlinestRet = Linear(lnY, lnX);
dlinestRet[0] = Math.Exp(dlinestRet[0]);
return dlinestRet;
}
#endregion
#region 指数函数拟合函数模型，公式为 y=c*m^x;输出为 c,m
static public double[] IndexEST(double[] y, double[] x)
{
double[] lnY = new double[y.Length];
double[] ratio;
for (int i = 0; i < y.Length; i++)
{
lnY[i] = Math.Log(y[i]);
}
ratio = Linear(lnY, x);
for (int i = 0; i < ratio.Length; i++)
{
if (i == 0)
{
ratio[i] = Math.Exp(ratio[i]);
}
}
return ratio;
}
#endregion
#region 相关系数R²部分
public static double Pearson(IEnumerable<double> dataA, IEnumerable<double> dataB)
{
int n = 0;
double r = 0.0;
double meanA = 0;
double meanB = 0;
double varA = 0;
double varB = 0;
int ii = 0;
using (IEnumerator<double> ieA = dataA.GetEnumerator())
using (IEnumerator<double> ieB = dataB.GetEnumerator())
{
while (ieA.MoveNext())
{
if (!ieB.MoveNext())
{
//throw new ArgumentOutOfRangeException("dataB", Resources.ArgumentArraysSameLength);
}
ii++;
//Console.WriteLine("FF00:: " + ii + " -- " + meanA + " -- " + meanB + " -- " + varA + " --- " + varB);
double currentA = ieA.Current;
double currentB = ieB.Current;
double deltaA = currentA - meanA;
double scaleDeltaA = deltaA / ++n;
double deltaB = currentB - meanB;
double scaleDeltaB = deltaB / n;
meanA += scaleDeltaA;
meanB += scaleDeltaB;
varA += scaleDeltaA * deltaA * (n - 1);
varB += scaleDeltaB * deltaB * (n - 1);
r += (deltaA * deltaB * (n - 1)) / n;
//Console.WriteLine("FF00:: " + ii + " -- " + meanA + " -- " + meanB + " -- " + varA + " --- " + varB);
}
if (ieB.MoveNext())
{
//throw new ArgumentOutOfRangeException("dataA", Resources.ArgumentArraysSameLength);
}
}
return (r / Math.Sqrt(varA * varB)) * (r / Math.Sqrt(varA * varB));
}
#endregion
#region 最小二乘法部分
#region 计算增广矩阵
static private double[] Cal_Guass(double[,] guass,int count)
{
double temp;
double[] x_value;
for (int j = 0; j < count; j++)
{
int k = j;
double min = guass[j,j];
for (int i = j; i < count; i++)
{
if (Math.Abs(guass[i, j]) < min)
{
min = guass[i, j];
k = i;
}
}
if (k != j)
{
for (int x = j; x <= count; x++)
{
temp = guass[k, x];
guass[k, x] = guass[j, x];
guass[j, x] = temp;
}
}
for (int m = j + 1; m < count; m++)
{
double div = guass[m, j] / guass[j, j];
for (int n = j; n <= count; n++)
{
guass[m, n] = guass[m, n] - guass[j, n] * div;
}
}
/* System.Console.WriteLine("初等行变换：");
for (int i = 0; i < count; i++)
{
for (int m = 0; m < count + 1; m++)
{
System.Console.Write("{0,10:F6}", guass[i, m]);
}
Console.WriteLine();
}*/
}
x_value= Get_Value(guass, count);
return x_value;
/*if (x_value == null)
Console.WriteLine("方程组无解或多解！");
else
{
foreach (double x in x_value)
{
Console.WriteLine("{0:F6}", x);
}
}*/
}
#endregion
#region 回带计算X值
static private double[] Get_Value(double[,] guass,int count)
{
double[] x = new double[count];
double[,] X_Array = new double[count, count];
int rank = guass.Rank;//秩是从0开始的
for (int i = 0; i < count; i++)
for (int j = 0; j < count; j++)
X_Array[i, j] = guass[i, j];
if (X_Array.Rank < guass.Rank)//表示无解
{
return null;
}
if (X_Array.Rank < count-1)//表示有多解
{
return null;
}
//回带计算x值
x[count - 1] = guass[count - 1, count] / guass[count-1, count-1];
for (int i = count - 2; i >= 0; i--)
{
double temp=0;
for (int j = i; j < count; j++)
{
temp += x[j] * guass[i, j];
}
x[i] = (guass[i, count] - temp) / guass[i, i];
}
return x;
}
#endregion
#region 得到数据的法矩阵,输出为发矩阵的增广矩阵
static private double[,] Get_Array(double[] y, double[] x, int n)
{
double[,] result = new double[n + 1, n + 2];
if (y.Length != x.Length)
{
throw (new Exception("两个输入数组长度不一！"));
//return null;
}
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
result[i, j] = Cal_sum(x, i + j);
}
result[i, n + 1] = Cal_multi(y, x, i);
}
return result;
}
#endregion
#region 累加的计算
static private double Cal_sum(double[] input,int order)
{
double result=0;
int length = input.Length;
for (int i = 0; i < length; i++)
{
result += Math.Pow(input[i], order);
}
return result;
}
#endregion
#region 计算∑(x^j)*y
static private double Cal_multi(double[] y,double[] x,int order)
{
double result = 0;
int length = x.Length;
for (int i = 0; i < length; i++)
{
result += Math.Pow(x[i], order) * y[i];
}
return result;
}
#endregion
#endregion
}
}
fuzhzh345 2017-06-08
- 打赏
- 举报
类1：
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace 高斯消元法
{
class Program
{
static void Main(string[] args)
{
/* double[,] xArray = new double[,]
{
{ 2.000000 ,-1.000000 , 3.000000, 1.000000},
{ 4.000000 , 2.000000 , 5.000000, 4.000000},
{ 1.000000 , 2.000000 , 0.000000 , 7.000000}
};*/
System.Diagnostics.Stopwatch sw = new System.Diagnostics.Stopwatch();
double[] y = new double[] { 29152.3, 47025.3, 86852.3, 132450.6, 200302.3, 284688.1, 396988.3 };
double[] x = new double[] { 1.24, 2.37, 5.12, 8.12, 12.19, 17.97, 24.99 };
// double[,] xArray;
double[] ratio;
double[] yy = new double[y.Length];
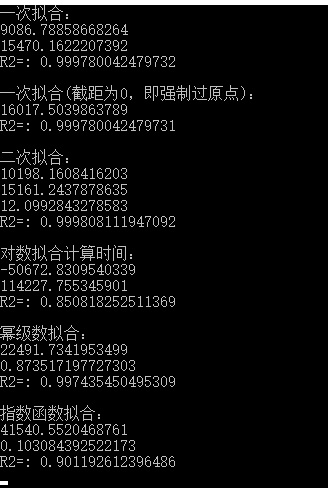
Console.WriteLine("一次拟合：");
sw.Start();
ratio = FittingFunct.Linear(y, x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
for (int i = 0; i < x.Length; i++)
{
yy[i] = ratio[0] + ratio[1] * x[i];
}
Console.WriteLine("R²=: " + FittingFunct.Pearson(y, yy) + "\r\n");
//Console.WriteLine("一次拟合计算时间：");
//Console.WriteLine(sw.ElapsedMilliseconds);
Console.WriteLine("一次拟合(截距为0，即强制过原点)：");
sw.Start();
ratio = FittingFunct.LinearInterceptZero(y, x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
for (int i = 0; i < x.Length; i++)
{
yy[i] = ratio[0] * x[i];
}
Console.WriteLine("R²=: " + FittingFunct.Pearson(y, yy) + "\r\n");
//Console.WriteLine("一次拟合计算时间：");
//Console.WriteLine(sw.ElapsedMilliseconds);
Console.WriteLine("二次拟合：");
sw.Start();
ratio = FittingFunct.TowTimesCurve(y, x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
for (int i = 0; i < x.Length; i++)
{
yy[i] = ratio[0] + ratio[1] * x[i] + ratio[2] * x[i] * x[i];
}
Console.WriteLine("R²=: " + FittingFunct.Pearson(y, yy) + "\r\n");
//Console.WriteLine("二次拟合计算时间：");
//Console.WriteLine(sw.ElapsedMilliseconds);
Console.WriteLine("对数拟合计算时间：");
sw.Start();
ratio = FittingFunct.LOGEST(y, x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
for (int i = 0; i < x.Length; i++)
{
yy[i] = ratio[1]*Math.Log10(x[i]) + ratio[0];
}
Console.WriteLine("R²=: " + FittingFunct.Pearson(y, yy) + "\r\n");
//Console.WriteLine("对数拟合计算时间：");
//Console.WriteLine(sw.ElapsedMilliseconds);
Console.WriteLine("幂级数拟合：");
sw.Start();
ratio=FittingFunct.PowEST(y,x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
for (int i = 0; i < x.Length; i++)
{
yy[i] = ratio[0] * Math.Pow(x[i], ratio[1]);
}
Console.WriteLine("R²=: " + FittingFunct.Pearson(y, yy) + "\r\n");
//Console.WriteLine("幂级数拟合计算时间：");
//Console.WriteLine(sw.ElapsedMilliseconds);
Console.WriteLine("指数函数拟合：");
sw.Start();
ratio = FittingFunct.IndexEST(y, x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
for (int i = 0; i < x.Length; i++)
{
yy[i] = ratio[0] * Math.Exp(x[i] * ratio[1]);
}
Console.WriteLine("R²=: " + FittingFunct.Pearson(y, yy));
//Console.WriteLine("指数函数拟合计算时间：");
//Console.WriteLine(sw.ElapsedMilliseconds);
Console.ReadKey();
}
}
}
fuzhzh345 2017-06-08
- 打赏
- 举报
拟合代码引用：http://download.csdn.net/detail/flyrp/5250732
相关系数R²的公式引用：http://blog.csdn.net/huwei2003/article/details/18553775（验证过）
1.一次线性、二次曲线、指数、对数、幂等函数拟合及相关系数R²的代码实现（指数函数拟合的相关系数R²和Excel有出入）；
2.一次线性的截距为0（即强制过原点）的代码实现；
3.代码三次乃至多项以上的函数拟合有问题，不会改，望有大神补充修改一下；
4.有没有大神补充一下二次曲线、指数这2个函数拟合时截距为0（即强制过原点）的拟合代码或者数学公式。
代码实现在Excel验证过！
相关系数R²的公式引用：http://blog.csdn.net/huwei2003/article/details/18553775（验证过）
1.一次线性、二次曲线、指数、对数、幂等函数拟合及相关系数R²的代码实现（指数函数拟合的相关系数R²和Excel有出入）；
2.一次线性的截距为0（即强制过原点）的代码实现；
3.代码三次乃至多项以上的函数拟合有问题，不会改，望有大神补充修改一下；
4.有没有大神补充一下二次曲线、指数这2个函数拟合时截距为0（即强制过原点）的拟合代码或者数学公式。
代码实现在Excel验证过！
xuzuning 2017-06-07
- 打赏
- 举报
不好意思，突然发现我写错了。应该这样
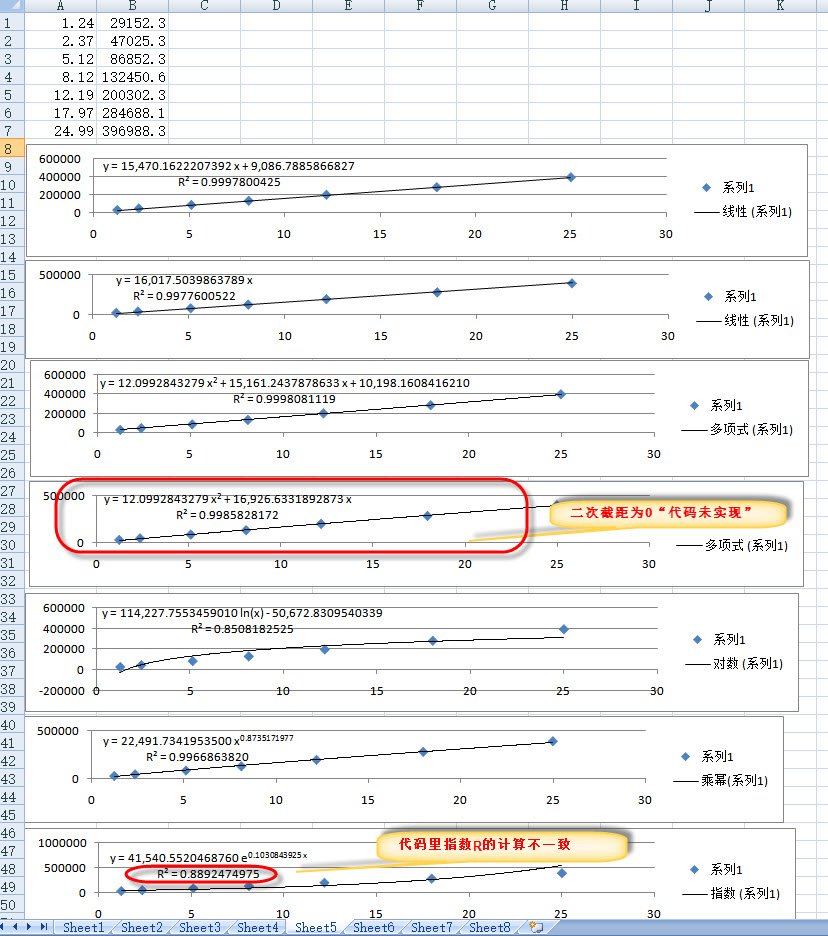
static void 相关系数(double[] x, double[] y, double[] ratio)
{
var 总平方和 = y.Select(p => p * p).Sum();
var 残差平方和 = x.Zip(y, (a, b) => Math.Pow(b - ratio.Select((p, i) => p * Math.Pow(a, i)).Sum(), 2)).Sum();
Console.WriteLine("相关系数：{0}\n", (总平方和 - 残差平方和) / 总平方和);
}
xuzuning 2017-06-07
- 打赏
- 举报
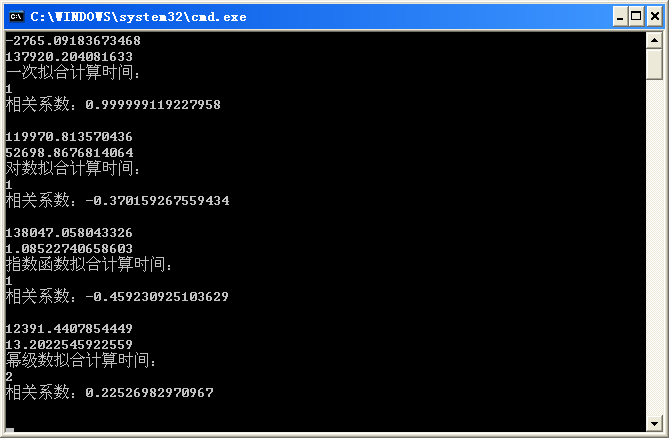
static void 相关系数(double[] x, double[] y, double[] ratio)
{
var 总平方和 = y.Select(p => p * p).Sum();
var 残差平方和 = x.Zip(y, (a, b) => b - ratio.Select((p, i) => p * Math.Pow(a, i)).Sum()).Sum();
Console.WriteLine("相关系数：{0}\n", 总平方和 / (总平方和 - 残差平方和));
}
fuzhzh345 2017-06-07
- 打赏
- 举报
这些功能Excel上都有，原理一模一样，现在需要C#的实现代码；
各函数的线性拟合，相关系数、截距为0（即强制过原点）等等。
各函数的线性拟合，相关系数、截距为0（即强制过原点）等等。
fuzhzh345 2017-06-07
- 打赏
- 举报
版主你要帮我写吗，他里面就有两个类
类1：
类2：
运行效果（就是没有相关系数R的计算，还有就是过原点）：
类1：
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace 高斯消元法
{
class FittingFunct
{
#region 多项式拟合函数,输出系数是y=a0+a1*x+a2*x*x+.........，按a0,a1,a2输出
static public double[] Polyfit(double[] y, double[] x, int order)
{
double[,] guass = Get_Array(y, x, order);
double[] ratio = Cal_Guass(guass, order + 1);
return ratio;
}
#endregion
#region 一次拟合函数，y=a0+a1*x,输出次序是a0,a1
static public double[] Linear(double[] y,double[] x)
{
double[] ratio = Polyfit(y, x, 1);
return ratio;
}
#endregion
#region 对数拟合函数,.y= c*(ln x)+b,输出为b,c
static public double[] LOGEST(double[] y, double[] x)
{
double[] lnX = new double[x.Length];
for (int i = 0; i < x.Length; i++)
{
if (x[i] == 0 || x[i] < 0)
{
throw (new Exception("正对非正数取对数！"));
return null;
}
lnX[i] = Math.Log(x[i]);
}
return Linear(y, lnX);
}
#endregion
#region 幂函数拟合模型, y=c*x^b,输出为c,b
static public double[] PowEST(double[] y, double[] x)
{
double[] lnX = new double[x.Length];
double[] lnY = new double[y.Length];
double[] dlinestRet;
for (int i = 0; i < x.Length; i++)
{
lnX[i] = Math.Log(x[i]);
lnY[i] = Math.Log(y[i]);
}
dlinestRet = Linear(lnY, lnX);
dlinestRet[0] = Math.Exp(dlinestRet[0]);
return dlinestRet;
}
#endregion
#region 指数函数拟合函数模型，公式为 y=c*m^x;输出为 c,m
static public double[] IndexEST(double[] y, double[] x)
{
double[] lnY = new double[y.Length];
double[] ratio;
for (int i = 0; i < y.Length; i++)
{
lnY[i] = Math.Log(y[i]);
}
ratio = Linear(lnY, x);
for (int i = 0; i < ratio.Length; i++)
{
ratio[i] = Math.Exp(ratio[i]);
}
return ratio;
}
#endregion
#region 最小二乘法部分
#region 计算增广矩阵
static private double[] Cal_Guass(double[,] guass,int count)
{
double temp;
double[] x_value;
for (int j = 0; j < count; j++)
{
int k = j;
double min = guass[j,j];
for (int i = j; i < count; i++)
{
if (Math.Abs(guass[i, j]) < min)
{
min = guass[i, j];
k = i;
}
}
if (k != j)
{
for (int x = j; x <= count; x++)
{
temp = guass[k, x];
guass[k, x] = guass[j, x];
guass[j, x] = temp;
}
}
for (int m = j + 1; m < count; m++)
{
double div = guass[m, j] / guass[j, j];
for (int n = j; n <= count; n++)
{
guass[m, n] = guass[m, n] - guass[j, n] * div;
}
}
/* System.Console.WriteLine("初等行变换：");
for (int i = 0; i < count; i++)
{
for (int m = 0; m < count + 1; m++)
{
System.Console.Write("{0,10:F6}", guass[i, m]);
}
Console.WriteLine();
}*/
}
x_value= Get_Value(guass, count);
return x_value;
/*if (x_value == null)
Console.WriteLine("方程组无解或多解！");
else
{
foreach (double x in x_value)
{
Console.WriteLine("{0:F6}", x);
}
}*/
}
#endregion
#region 回带计算X值
static private double[] Get_Value(double[,] guass,int count)
{
double[] x = new double[count];
double[,] X_Array = new double[count, count];
int rank = guass.Rank;//秩是从0开始的
for (int i = 0; i < count; i++)
for (int j = 0; j < count; j++)
X_Array[i, j] = guass[i, j];
if (X_Array.Rank < guass.Rank)//表示无解
{
return null;
}
if (X_Array.Rank < count-1)//表示有多解
{
return null;
}
//回带计算x值
x[count - 1] = guass[count - 1, count] / guass[count-1, count-1];
for (int i = count - 2; i >= 0; i--)
{
double temp=0;
for (int j = i; j < count; j++)
{
temp += x[j] * guass[i, j];
}
x[i] = (guass[i, count] - temp) / guass[i, i];
}
return x;
}
#endregion
#region 得到数据的法矩阵,输出为发矩阵的增广矩阵
static private double[,] Get_Array(double[] y, double[] x, int n)
{
double[,] result = new double[n + 1, n + 2];
if (y.Length != x.Length)
{
throw (new Exception("两个输入数组长度不一！"));
//return null;
}
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
result[i, j] = Cal_sum(x, i + j);
}
result[i, n + 1] = Cal_multi(y, x, i);
}
return result;
}
#endregion
#region 累加的计算
static private double Cal_sum(double[] input,int order)
{
double result=0;
int length = input.Length;
for (int i = 0; i < length; i++)
{
result += Math.Pow(input[i], order);
}
return result;
}
#endregion
#region 计算∑(x^j)*y
static private double Cal_multi(double[] y,double[] x,int order)
{
double result = 0;
int length = x.Length;
for (int i = 0; i < length; i++)
{
result += Math.Pow(x[i], order) * y[i];
}
return result;
}
#endregion
#endregion
}
}
类2：
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace 高斯消元法
{
class Program
{
static void Main(string[] args)
{
/* double[,] xArray = new double[,]
{
{ 2.000000 ,-1.000000 , 3.000000, 1.000000},
{ 4.000000 , 2.000000 , 5.000000, 4.000000},
{ 1.000000 , 2.000000 , 0.000000 , 7.000000}
};*/
System.Diagnostics.Stopwatch sw = new System.Diagnostics.Stopwatch();
//double[] y = new double[] { 29152.3, 47025.3, 86852.3, 132450.6, 200302.3, 284688.1, 396988.3 };
//double[] x = new double[] { 1.24, 2.37, 5.12, 8.12, 12.19, 17.97, 24.99 };
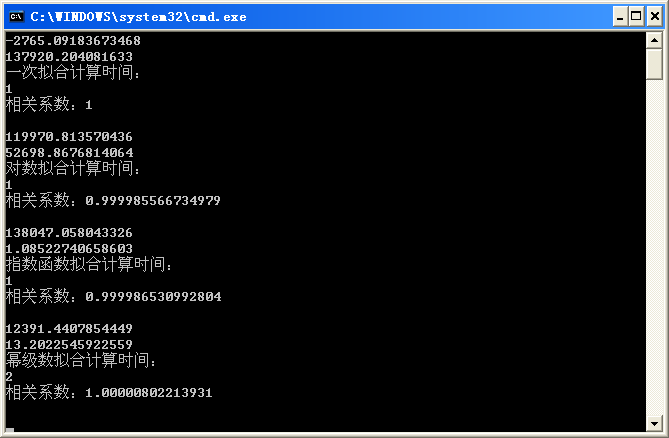
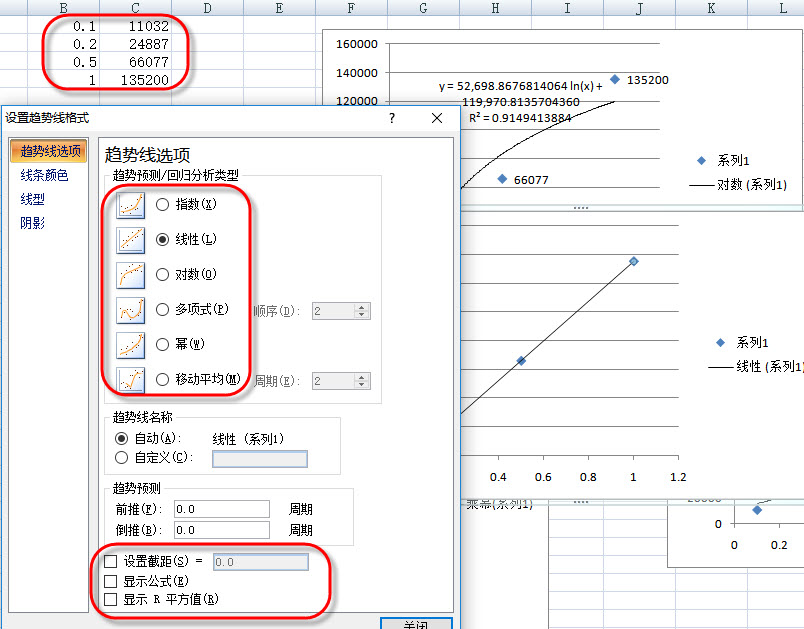
double[] x = new double[] { 0.1, 0.2, 0.5, 1.0 };
double[] y = new double[] { 11032, 24887, 66077, 135200 };
// double[,] xArray;
double[] ratio;
sw.Start();
ratio = FittingFunct.Linear(y, x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
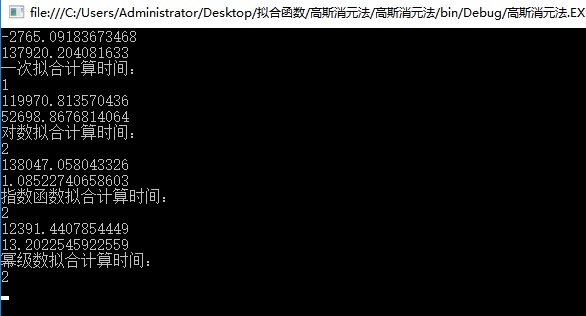
Console.WriteLine("一次拟合计算时间：");
Console.WriteLine(sw.ElapsedMilliseconds);
sw.Start();
ratio = FittingFunct.LOGEST(y, x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
Console.WriteLine("对数拟合计算时间：");
Console.WriteLine(sw.ElapsedMilliseconds);
sw.Start();
ratio=FittingFunct.PowEST(y,x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
Console.WriteLine("指数函数拟合计算时间：");
Console.WriteLine(sw.ElapsedMilliseconds);
sw.Start();
ratio = FittingFunct.IndexEST(y, x);
sw.Stop();
foreach (double num in ratio)
{
Console.WriteLine(num);
}
Console.WriteLine("幂级数拟合计算时间：");
Console.WriteLine(sw.ElapsedMilliseconds);
Console.ReadKey();
}
}
}
运行效果（就是没有相关系数R的计算，还有就是过原点）：
xuzuning 2017-06-06
- 打赏
- 举报
我没下载分，下不了你的文件
fuzhzh345 2017-06-06
- 打赏
- 举报
我想要直接代码实现的，这原理没理解，写不出来~~
xuzuning 2017-06-06
- 打赏
- 举报
