查找曲线中的拐点

[小海贼]

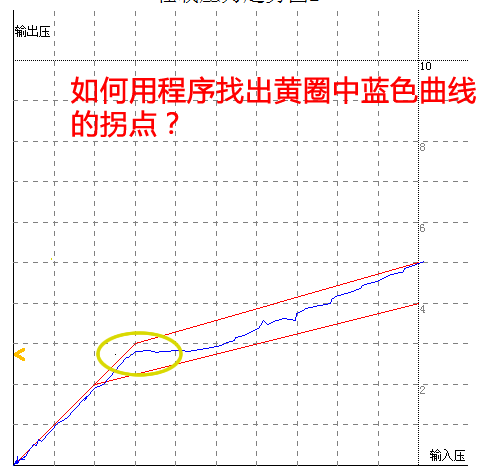
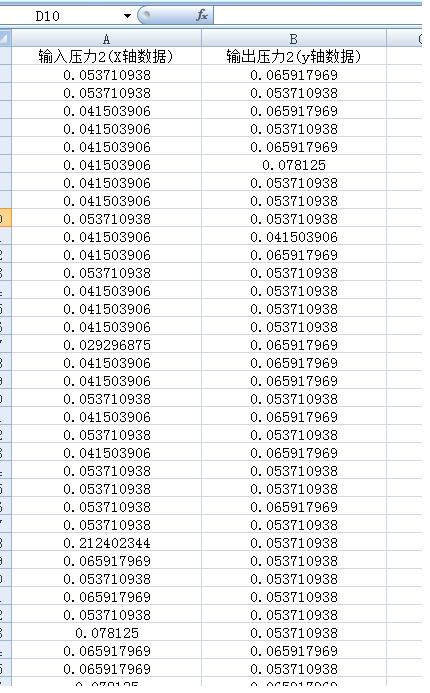
图片中的蓝色曲线是一些离散点连起来的曲线图，这些离散点的X轴值和Y轴值见我的Excel文件。


现在我想通过程序C#或Sql 脚本（实际数据是存在数据库中的），分析出这个拐点，上面图中的黄色圈圈的是我用目测方式画出来的，但如何用程序来分析出来？
另外这些离散的点是从设备上高速采集下来的（每15毫秒一个点），有干扰信号在。

下面链接是我的实际离散点的数据，是个excel文件，希望有大神能帮忙提点提点，感谢！
http://pan.baidu.com/s/1o8hvQqe

[ilikeff8]

这是要求切线，曲率，还是求导来着，忘了

[ilikeff8]

我想最简单的就是看y值是不是下降了

[ilikeff8]

如果一段时间内y相对参考点一直呈下降趋势，则认为是拐点

[xuzuning]

对原始数据做多项式拟合可得9阶或11阶多项式，代入后可知拟合度是不错的

对拟合多项式求导，并令导函数为0
即可求出所有的拐点

[小海贼]

引用 4 楼 xuzuning 的回复:

对原始数据做多项式拟合可得9阶或11阶多项式，代入后可知拟合度是不错的 对拟合多项式求导，并令导函数为0 即可求出所有的拐点

非常感谢您的提点，这两天一直在沿着你的提示在研究，也基本上搞灵清了（之前什么导数，多项式都忘得得干干净净了，重新恶补了下）； 现在我已经得到用于曲线拟合的多项式 函数（最高为7阶）并推导出它的二阶导函数，但令导函数为0时求X值没求出来，我用的是matlab求的； 我用solve求解这个线性方程； >>solve('- (141346384467264249*x^5)/2361183241434822606848 + (65318965582253535*x^4)/9223372036854775808 - (38862562480454115*x^3)/288230376151711744 + (8476420589762919*x^2)/9007199254740992 - (5664416154594873*x)/2251799813685248 + 4015725232555215/2251799813685248=0','x','MaxDegree',5) 说明：【- (141346384467264249*x^5)/2361183241434822606848 + (65318965582253535*x^4)/9223372036854775808 - (38862562480454115*x^3)/288230376151711744 + (8476420589762919*x^2)/9007199254740992 - (5664416154594873*x)/2251799813685248 + 4015725232555215/2251799813685248=0】 这个就是我的二阶导函数，我求它=0； 计算后的信息为： root(z^5 - (5573885063018968320*z^4)/47115461489088083 + (8163131072817438720*z^3)/3624266268391391 - (740680933027603546112*z^2)/47115461489088083 + (152296688044114706432*z)/3624266268391391 - 1403597700483939041280/47115461489088083, z, 1) root(z^5 - (5573885063018968320*z^4)/47115461489088083 + (8163131072817438720*z^3)/3624266268391391 - (740680933027603546112*z^2)/47115461489088083 + (152296688044114706432*z)/3624266268391391 - 1403597700483939041280/47115461489088083, z, 2) root(z^5 - (5573885063018968320*z^4)/47115461489088083 + (8163131072817438720*z^3)/3624266268391391 - (740680933027603546112*z^2)/47115461489088083 + (152296688044114706432*z)/3624266268391391 - 1403597700483939041280/47115461489088083, z, 3) root(z^5 - (5573885063018968320*z^4)/47115461489088083 + (8163131072817438720*z^3)/3624266268391391 - (740680933027603546112*z^2)/47115461489088083 + (152296688044114706432*z)/3624266268391391 - 1403597700483939041280/47115461489088083, z, 4) root(z^5 - (5573885063018968320*z^4)/47115461489088083 + (8163131072817438720*z^3)/3624266268391391 - (740680933027603546112*z^2)/47115461489088083 + (152296688044114706432*z)/3624266268391391 - 1403597700483939041280/47115461489088083, z, 5) 这个应该怎么理解？ 我网上查了，没什么资料可以参考；麻烦您再给点指导。谢谢。

[xuzuning]

9阶拟合多项式的二阶导函数是一个7阶的多项式 但是高于4次的多项式是没有直接的数学解法的 一般手工计算是通过因式分解将其化为若干个低次多项式的乘积，分别求解 但是用机器很难实现这种因式分解的算法 况且实际应用中也只是要得到他的一组数值解 所以一般可用迭代器求解 f''(x) = 0 就是找出当自变量 x 为何值时，二阶导函数 f''(x) 的值为 0

[xuzuning]

其实这个算法就和从拟合多项式画出拟合曲线是一样的

[小海贼]

引用 6 楼 xuzuning 的回复:

9阶拟合多项式的二阶导函数是一个7阶的多项式 但是高于4次的多项式是没有直接的数学解法的 一般手工计算是通过因式分解将其化为若干个低次多项式的乘积，分别求解 但是用机器很难实现这种因式分解的算法 况且实际应用中也只是要得到他的一组数值解 所以一般可用迭代器求解 f''(x) = 0 就是找出当自变量 x 为何值时，二阶导函数 f''(x) 的值为 0

您的意思是让我for循环遍历x的值，取出那些y=0的x； 但因为我的x轴数据本身是离散的，不一定存在

引用 7 楼 xuzuning 的回复:

其实这个算法就和从拟合多项式画出拟合曲线是一样的

是的，我用你说的方法推出了几个拐点； 我遍历x的离散数据，分别得到导函数的值。最后查找临界的2个值一个是小于0，一个大于0，则标识这2个临界的x值中间必定存在一个让导函数为0的值； 后来在matlab也找到了解决办法，结果与之前迭代法求的同样结果； 整个推导过程算是完成了，非常感谢版主！ 不过得到的拐点值和我肉眼判断的拐点值有区别，我正试着用其它方法去算。

[xuzuning]

其实我也有过与你相同的误解 所谓拐点，实际是曲线凸段与凹段的分界点，相当于你主贴图中那个黄圈与曲线的交点 并非凸段或凹段的峰值点 而这个峰值点的求法，我想可能是计算出两拐点间曲线上各的切线，当某点的切线与拐点间连线平行时，则该点就应是所求点了

[小海贼]

引用 9 楼 xuzuning 的回复:

其实我也有过与你相同的误解 所谓拐点，实际是曲线凸段与凹段的分界点，相当于你主贴图中那个黄圈与曲线的交点 并非凸段或凹段的峰值点 而这个峰值点的求法，我想可能是计算出两拐点间曲线上各的切线，当某点的切线与拐点间连线平行时，则该点就应是所求点了

是的，我求出来的拐点就是在那个黄圈与曲线的交点处。 主要项目比较急，所以我现在用比较简单的判断方法先应付着（x,y的差值比较），等应付完再想想如何用成熟的数学模型去解决这个问题。 再次感谢版主，让我学到了不少。