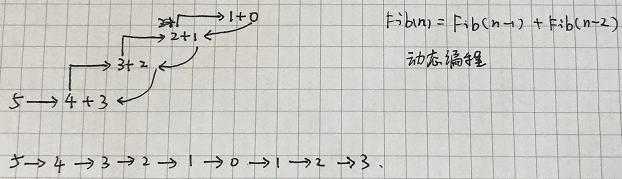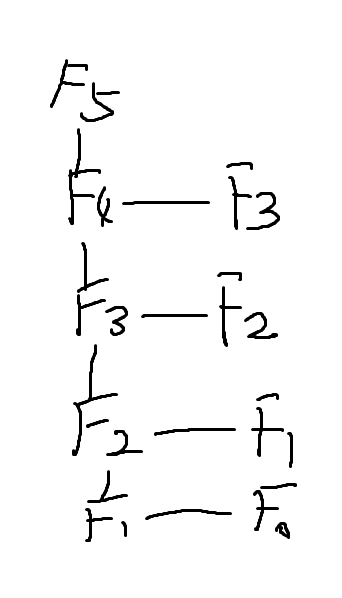Python 递归原理（斐波那契数列为例）的疑问

[wu5261092]

各位好！
最近在学习递归的时候碰到了一些运行原理上的疑问，特来此请教大家

代码如下
def fastFib(n,memo):
global numCalls
numCalls += 1
print('fib called with',n)
if not n in memo:
memo[n] = fastFib(n-1,memo) + fastFib(n-2,memo)
return memo[n]

def fastFib1(n,memo):
global numCalls
numCalls = 0
res = fastFib(n,memo)
print('fastFib of',n,'=',res,', numCalls =',numCalls)

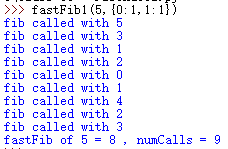
运行结果图如下


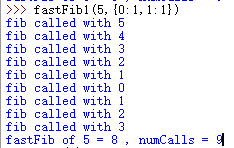
现有一个问题，描述如下表所示


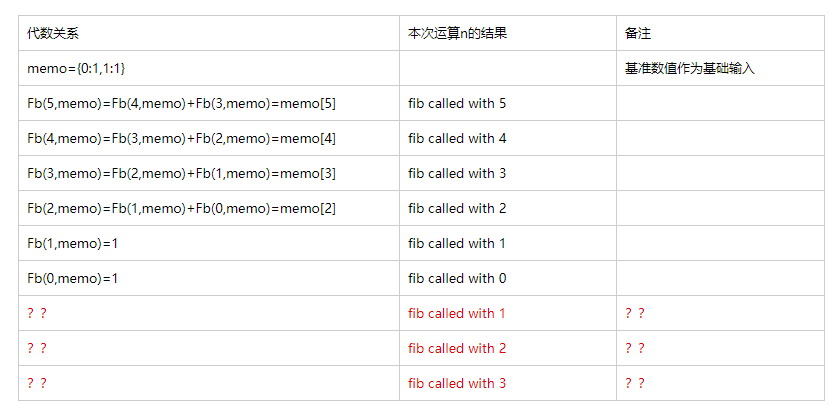
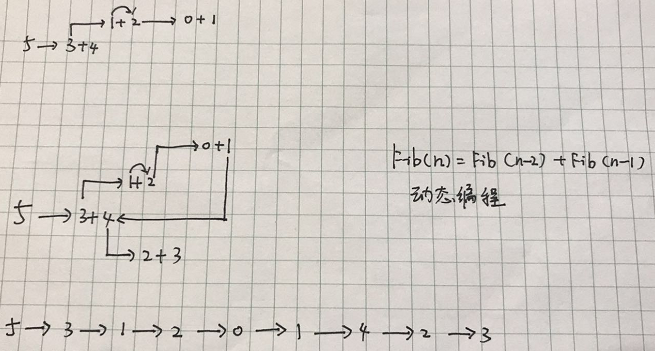
为啥最后还要再调用一下n=1,2,3的情况呢？我推测是
Fb(5,memo)=Fb(4,memo)+Fb(3,memo)
Fb(4,memo)=Fb(3,memo)+Fb(2,memo)
Fb(3,memo)=Fb(2,memo)+Fb(1,memo)

但Fb(1,memo)不是已经计算过一次了吗？为啥还要再计算一次？

求助各位详细描述一下Python中递归的原理

感谢！

[欢乐的小猪]

递归是依赖计算机的一种数据结构——栈来实现的。它最重要的特点就是先入后出，后入先出。
你调用f5，需要将f4和f3压栈，然后f4出栈，把f3和f2压栈，。。。。。

[欢乐的小猪]

你可以通过调换n-1和n-2的顺序，如：f(n)=f(n-2)+f(n-1)来更好的理解栈结构

[wu5261092]

感谢你的及时回复！为了弄清楚这个问题，我这些天一直在查找相关的资料，现在弄懂啦 谢谢你！

引用 2 楼 hbu_pig 的回复:

你可以通过调换n-1和n-2的顺序，如：f(n)=f(n-2)+f(n-1)来更好的理解栈结构

Fib(5)-->return Fib(4)+Fib(3)，这时内存将打开三个抽屉，Fib(5)是一个大抽屉，里头包含了Fib(4)，Fib(3)两个小抽屉；

然后根据顺序，先运行Fib(4)，return Fib(3)+Fib(2)，在Fib(4)这个抽屉里又开了两个小抽屉，Fib(3)和Fib(2)；

就这么一直运行，直到Fib(2)开了两个小抽屉，一个Fib(1),一个Fib(0)，这两个小抽屉打开，发现真正的值，所以可以立即关上。

此时Fib(2)的值也知道了，也可以关上这个抽屉。与此同时，记录下Fib(2)的值，下次就不用再打开两个小抽屉看了。

但Fib(3)=Fib(2)+Fib(1)；还有一个Fib(1)的屉子需要关上，因此打开-->发现值后-->关上。与此同时，记录下Fib(3)的值，下次就不用再打开里头的小抽屉看了。

Fib(4)= Fib(3)+Fib(2)；Fib(3)的屉子关上了，里头还有一个Fib(2)的, 但我们已经记录好Fib(2)的值了，因此只需打开Fib(2)的抽屉，不必打开内部的小抽屉，直接可以知道值。

Fib(5)= Fib(4)+Fib(3)；Fib(4)的屉子关上了，里头还有一个Fib(3)的, 但我们已经记录好Fib(3)的值了，因此只需打开Fib(3)的抽屉，不必打开内部的小抽屉，直接可以知道值。

打开的屉子数就是占用的内存数




换过来以后也理解了