33,027
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享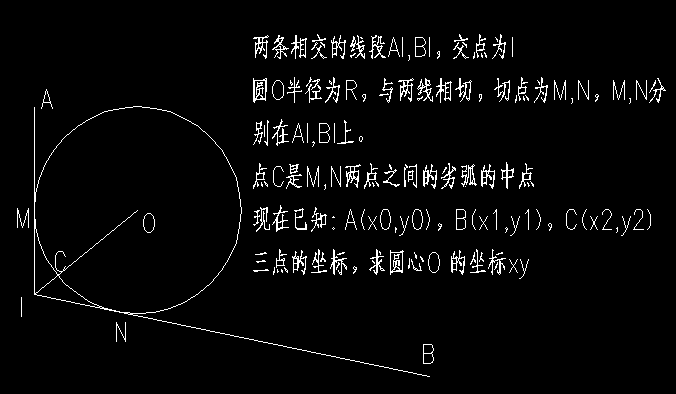

 今天有点时间大概算了下,如果楼主可以就自行化解,老夫过几日再看看
今天有点时间大概算了下,如果楼主可以就自行化解,老夫过几日再看看
// pppl.cpp : 定义控制台应用程序的入口点。
//
/*********************************************************************************
* Copyright(C),;
* FileName: pppl.cpp
* Author: lizhq;
* Date: 2019-1-18
* Description: 已知相交线段的两个发散侧端点及交点侧倒角圆弧的中点及圆弧半径,
求该曲线(两条线段+圆弧),
转化为求圆心坐标,圆心坐标求出后,求曲线就很简单了。
*********************************************************************************/
#include "math.h"
#include <vector>
#define min(a,b) (((a) < (b)) ? (a) : (b))
#define max(a,b) (((a) > (b)) ? (a) : (b))
#define eps (1e-12)
#define PI (3.1415926535897932384626)
#define R2D(rad) (rad / PI * 180.0)
#define D2R(ang) (ang / 180.0 * PI)
class CLPoit
{
public:
double x;
double y;
CLPoit()
{
y = 0.;
x = 0.;
}
CLPoit(double xx, double yy)
{
y = yy;
x = xx;
}
};
class CLArc
{
public:
double x;
double y;
double r;
double staRadian;
double sweepRadian;
CLArc()
{
y = 0.;
x = 0.;
r = 0.;
staRadian = 0.;
sweepRadian = 0.;
}
CLArc(const CLPoit& c, double rr, double sta, double swp)
{
x = c.x;
y = c.y;
r = rr;
staRadian = sta;
sweepRadian = swp;
}
CLArc(double xx, double yy, double rr, double sta, double swp)
{
x = xx;
y = yy;
r = rr;
staRadian = sta;
sweepRadian = swp;
}
void set(const CLPoit& c, double rr, double sta, double swp)
{
x = c.x;
y = c.y;
r = rr;
staRadian = sta;
sweepRadian = swp;
}
void set(double xx, double yy, double rr, double sta, double swp)
{
x = xx;
y = yy;
r = rr;
staRadian = sta;
sweepRadian = swp;
}
void getLinePts(std::vector<CLPoit>& pts, int count)
{
pts.clear();
if (count < 2)
return;
CLPoit pt;
double argRad = sweepRadian / (count - 1);
for (int i = 0; i < count; i++)
{
pt.x = r*cos((staRadian + argRad*double(i))) + x;
pt.y = r*sin((staRadian + argRad*double(i))) + y;
pts.push_back(pt);
}
}
};
double dis(const CLPoit& a, const CLPoit& b)
{
return sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
}
bool getQieDian(CLPoit& tangPt, const CLPoit& p, const CLPoit& o, double r, bool nsz)
{
double m = p.x, n = p.y;
double a = o.x, b = o.y;
// 点到圆心距离的平方
double d2 = (m - a) * (m - a) + (n - b) * (n - b);
// 点到圆心距离
double d = sqrt(d2);
if (d < r - eps)
return false;
if (d < r + eps)
{
tangPt = p;
return true;
}
// 半径的平方
double r2 = r * r;
// 点到切点距离
double l = sqrt(d2 - r2);
// 点->圆心的单位向量
double x0 = (a - m) / d;
double y0 = (b - n) / d;
// 计算切线与点心连线的夹角
double f = asin(r / d);
// 向正反两个方向旋转单位向量
if (!nsz) f = -f;
double x1 = x0 * cos(f) - y0 * sin(f);
double y1 = x0 * sin(f) + y0 * cos(f);
// 得到新座标
tangPt.x = x1 * l + m;
tangPt.y = y1 * l + n;
return true;
}
double getRadian(const CLPoit& p1, const CLPoit& p2)
{
double radian_temp;
double xx, yy;
xx = p2.x - p1.x;
yy = p2.y - p1.y;
if (xx == 0.0)
radian_temp = PI / 2.0;
else
radian_temp = atan(fabs(yy / xx));
if ((xx < 0.0) && (yy >= 0.0))
radian_temp = PI - radian_temp;
else if ((xx < 0.0) && (yy < 0.0))
radian_temp = PI + radian_temp;
else if ((xx >= 0.0) && (yy < 0.0))
radian_temp = PI * 2.0 - radian_temp;
return (radian_temp);
}
int getMinValIdx(double& minVal, const std::vector<CLPoit>& pts, const CLPoit& ptL, const CLPoit& ptM, const CLPoit& ptR, double r, bool nszxz)
{
int idx = -1;
minVal = DBL_MAX;
for (size_t i = 0; i < pts.size(); i++)
{
auto& ori = pts[i];
CLPoit qd1, qd2;
if (!getQieDian(qd1, ptL, ori, r, nszxz) || !getQieDian(qd2, ptR, ori, r, !nszxz))
continue;
double l1 = dis(qd1, ptM);
double l2 = dis(qd2, ptM);
double dLen = fabs(l1 - l2);
if (dLen < minVal)
{
minVal = dLen;
idx = i;
}
}
return idx;
}
void getAllLen(CLPoit& ori, const CLPoit& ptL, const CLPoit& ptM, const CLPoit& ptR, double r)
{
std::vector<double> lens;
double staRadian = getRadian(ptM, ptL);
double swRadian = getRadian(ptM, ptR) - staRadian;
if (swRadian > PI) swRadian -= 2 * PI;
else if (swRadian < -PI) swRadian += 2 * PI;
if (fabs(swRadian) < eps || fabs(fabs(swRadian) - PI) < eps)
{
//三点共线,无需找圆心
ori = ptM;
return;
}
bool nszxz = (swRadian > 0);
CLArc arc(ptM, r, staRadian, swRadian);
double deg = fabs(R2D(swRadian));
int count = (deg > 10.0) ? int(deg + 0.5) : 10;
std::vector<CLPoit> pts;
arc.getLinePts(pts, count);
for (int i = 0; i < count; i++)
{
ori = pts[i];
double dLen = -1.0;
CLPoit qd1, qd2;
if( getQieDian(qd1, ptL, ori, r, nszxz) && getQieDian(qd2, ptR, ori, r, !nszxz))
{
double l1 = dis(qd1, ptM);
double l2 = dis(qd2, ptM);
dLen = fabs(l1 - l2);
}
lens.push_back(dLen);
}
}
// 使用如下测试数据测试时出现死循环
// double r = 8000;
// CLPoit p1(-48248.5749, -14687.7393);
// CLPoit p2(-77030.8830, -6882.3034);
// CLPoit p3(-78825.9401, 6136.8982);
// 经分析是swRadian值过小时(e-15数量级),迭代过程中其值不再减小,造成死循环
// 推断可能与编译环境及操作系统位数相关,在不清楚具体原因的情况下,为避免死循环
// 应当增加判断,若swRadian的绝对值不再继续减小时,应当跳出while循环
int getOriPoint(CLPoit& ori, const CLPoit& ptL, const CLPoit& ptM, const CLPoit& ptR, double r)
{
//getAllLen(ori, ptL, ptM, ptR, r);
ori = ptM;
double staRadian = getRadian(ptM, ptL);
double swRadian = getRadian(ptM, ptR) - staRadian;
if (swRadian > PI) swRadian -= 2 * PI;
else if (swRadian < -PI) swRadian += 2 * PI;
if (fabs(swRadian) < eps || fabs(fabs(swRadian) - PI) < eps)
return 1; //三点共线,无需找圆心
// 点ptL到最终圆弧的切线的旋转方向
bool nszxz = (swRadian > 0);
//将圆弧划分成最少10等份(11个点);
std::vector<CLPoit> pts;
CLArc arc(ptM, r, staRadian, swRadian);
double deg = fabs(R2D(swRadian));
int count = (deg > 10.0) ? int(deg + 0.5) + 1 : 11;
arc.getLinePts(pts, count);
if (pts.empty())
return 3;
double lastSWRadian = swRadian;
double minVal = 0.0;
int idx, perIdx, nexIdx;
while (dis(pts.front(), pts.back()) > eps)
{
// 获取最小值及对应点的索引值;
idx = getMinValIdx(minVal, pts, ptL, ptM, ptR, r, nszxz);
if (idx < 0)
return 2;
ori = pts[idx];
if (minVal < eps)
{
break;
}
//取最小值两侧的点,将圆弧划分成4等份(5个点)进行迭代计算
perIdx = max(idx - 1, 0);
nexIdx = min(idx + 1, pts.size() - 1);
staRadian = getRadian(ptM, pts[perIdx]);
swRadian = getRadian(ptM, pts[nexIdx]) - staRadian;
if (swRadian > PI) swRadian -= 2 * PI;
else if (swRadian < -PI) swRadian += 2 * PI;
// 精度问题造成循环时,跳出循环(此时不判断精度,直接判==);
if (lastSWRadian == swRadian)
break;
lastSWRadian = swRadian;
arc.set(ptM, r, staRadian, swRadian);
arc.getLinePts(pts, 5);
}
//校验;
CLPoit qd1, qd2;
if (!getQieDian(qd1, ptL, ori, r, nszxz) || !getQieDian(qd2, ptR, ori, r, !nszxz))
return 2;
minVal = fabs(dis(qd1, ptM) - dis(qd2, ptM));
if (minVal < 1e-6)//校验精度值可降低要求;
{
return 0;
}
return 2;
}
void Test()
{
double r = 8000;
CLPoit p1(-48248.5749, -14687.7393);
CLPoit p2(-77030.8830, -6882.3034);
CLPoit p3(-78825.9401, 6136.8982);
CLPoit ori;
int retVal = getOriPoint(ori, p1, p2, p3, r);
}
int main()
{
Test();
return 0;
}