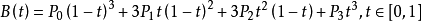最近写个小游戏,有方块移动的动画,线性动画显得有些生硬,想用贝塞尔实现非线性动画。
如这个网址的图示:http://cubic-bezier.com/#.43,.04,.11,1.42
但是遇到个问题:
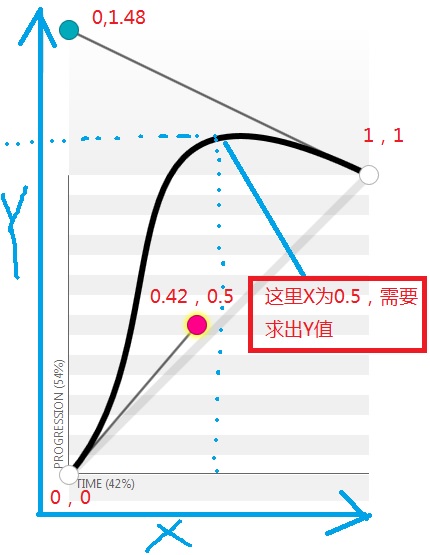
上面网站图示,是以x轴表示时间,y表示移动位置
查到的贝塞尔公式是:
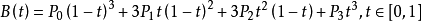 问题1:公式中的t到底是啥?
问题1:公式中的t到底是啥?
看起来网站中图示和公式,好像一个是二维的,一个是一维的。
问题2:可不可以这么理解,上面网址图示,是两个贝塞尔公式的结果?
问题3(主要):我想如网站中图示,代入x值求出对应的y值。应该怎么做?求给个算法
我主要是想,分别代入0.1 0.2 0.3 ... 1.0,求出动画中方块的位置,10帧。
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享