图解四色定理
一、概述
1852年,英国数学家法兰西斯.古德里最先提出四色猜想:“任何一张地图只用4种颜色就能使具有共同边界的国家着不同颜色”。
1976年,数学家凯尼斯.阿佩尔和沃夫冈.哈肯采用“放电法”程式、借助计算机运行1200小时验证,首次证明了四色定理。
但如此简洁的问题描述,与如此复杂的证明过程严重违和,一直有人希望能够找到更简单的、无需借助计算机的证明过程。
本文尝试论述一种直接的、无需借助计算机验算的四色定理证明。
二、关键概念
1) 正规地图
正规地图是指:没有1个国家包围其它国家,或没有3个以上国家相遇于1点的地图为正规地图(维基百科中也称为三度图)。
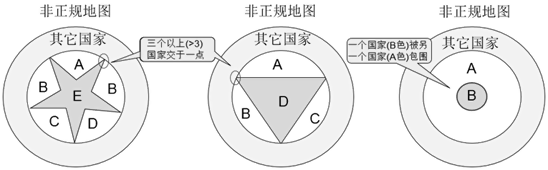
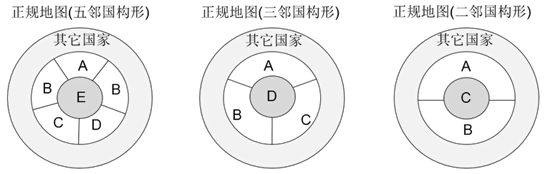
如上图所示,国家数量相同,在地图中的位置也相同的情况下,正规地图的着色数量一定不少于非正规地图。本文提到的地图默认指正规地图。
2) 不可避免构形
1878年,数学家阿尔弗雷德.布雷.肯普(Alfred Kempe)发布了一份四色定理证明。肯普在证明中阐述了两个重要概念,一直被视为证明四色定理的关键。第一个概念是“不可避免构形”,在任意正规地图中至少有1个国家具有2、3、4或5个邻国,不存在每个国家都有>=6个邻国的正规地图,也就是说,二、三、四或五邻国“构形”是不可避免的,每张地图中都必然含有这4种不可避免构形中的1个或多个。
证明过程引用了欧拉公式(v:顶点-e:边+r:面=2),得出任意平面地图中至少存在1个国家,其邻国数量<=5:
(1) 欧拉公式: v-e+r=2;
(2) 平面地图: 3*v<=2*e;
(3) 将欧拉公式代入公式(2)得: 3*r-e>=6;
(4) 假设地图中每个面平均有x条边,有: x*r=2*e;
(5) 将(4)代入(3)得: 6*r-x*r>=12,从而得平均边数: x<6;
因此,任意平面地图中一定至少存在1个国家,其邻国数量<=5;
3) 构形可约
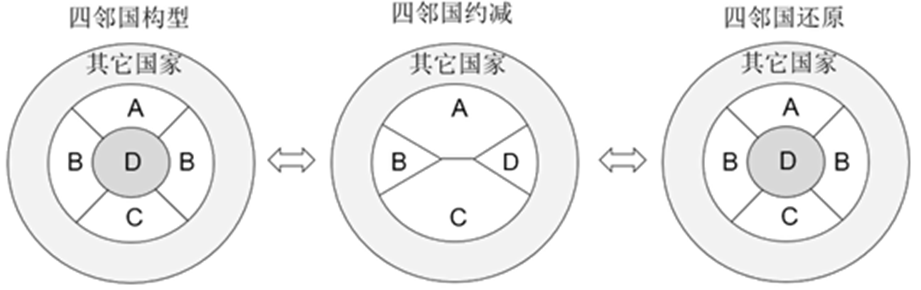
肯普提出的另一个概念是“可约”,即对不可避免构形(二、三、四、五邻国构形)中心的国家做任意约减、恢复操作时,不会增加地图的着色数量。
在持续约减不可避免构形中心的国家时,地图中其余的>=6邻国构形的相邻国家数量会降低,剩余的国家数量也会逐渐减少,最终会得到一份国家数量有限、且仅包含不可避免构形的地图。如果约减到最终的地图是四色足够的,那么对约减地图做逆序恢复操作,则恢复到初始状态的地图也一定四色足够的。
二、三邻国构形约减、恢复区域中心的国家并不会影响地图其它区域着色。被约减的四邻国构形在恢复时,可能会影响地图上的其它区域着色,但是利用肯普变换可以保证并不增加地图的着色数量。
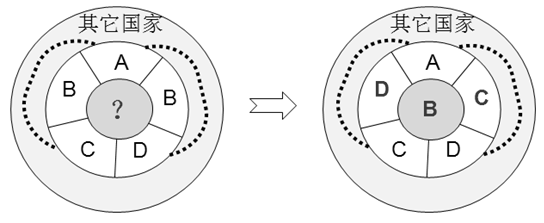
肯普在论文中描述五邻国构形区域也一定可约。如下图所示,如果约减后的构形区域5个邻国已经占满4种颜色,当不存在A-C、或者不存在A-D肯普链时,可将A色换着C、D色来恢复五邻国构形,当同时存在A-C、A-D两条肯链时,可按如下方式恢复五邻国构形(保持五邻国构形区域6个国家着4色、且不增加地图其它区域着色数量)。
4) 希伍德反例和五色定理
1890年,珀西.约翰.希伍德(Heawood)指出“肯普链”方法中的缺陷,并构造出无法使用肯普链变换着4色的局部五邻国构形地图实例,称为希伍德反例。
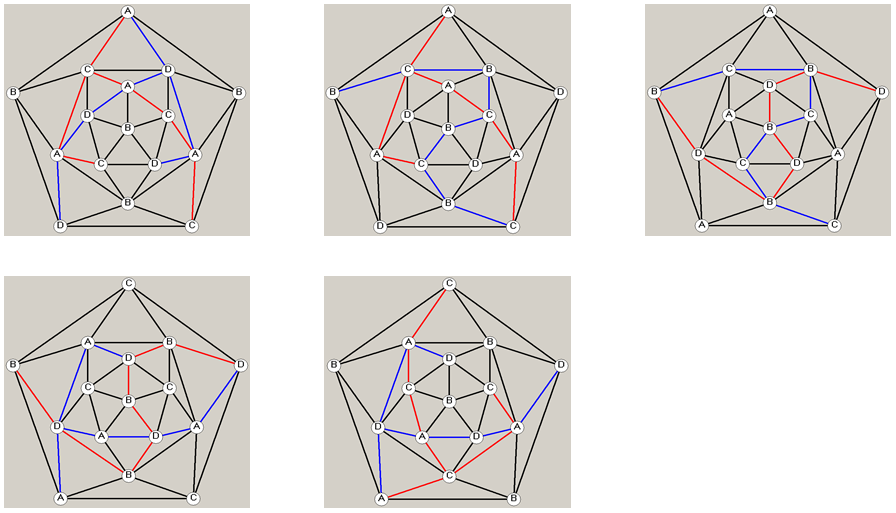
在希伍德构造的最小16国反例图中,目标五邻国构形周围的5个相邻国家,存在A-C与A-D两条“交叉”肯普链。对该地图局部构形周围的5个邻国使用肯普链变换着色,4种颜色在构形周围的5个邻国中恰好能循环往复,无法降到3种颜色,从而无法证明该五邻国构形区域(共6个国家)可被着4色。
对于该缺陷,肯普未能给出修复策略,因此四色猜想惜未得证。但相对较弱的五色定理命题由此得证。
希伍德同时提出猜想:在任意可定向曲面上,最多只用
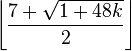
种颜色就能为任意的地图染色,其中k是曲面的亏格。当k=0的时候,这个猜想就变成了四色猜想。当地图中存在“飞地”时(地图中某两个不相邻的地区属于同一个国家,必须着同色),有K≥1。在1968年,杰拉德.格尔和J.W.T.杨格斯最终证明了这个猜想在k≥1时的情况。
直到1976年,数学家凯尼斯.阿佩尔和沃夫冈.哈肯采用“放电法”程式,经过计算机1200小时的验证,首次得到一个完全的证明,四色猜想也终于成为四色定理。
这是首个主要借助计算机证明的定理,一开始未被普遍接受,因为大众认为这个证明无法被直接验证。尽管随着计算机的普及,人们对计算机辅助证明更能接受,但仍有人希望能够找到简洁的、不借助计算机的证明过程。
三、证明过程
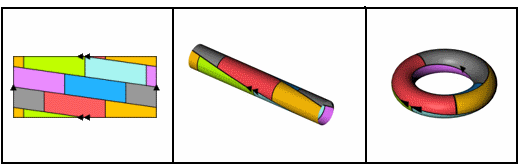
下图为希伍德在亏格为1的地图上构造出7个两两相邻国家的示意。
借鉴该方法,我们尝试分析五邻国构形的最小着色数量。
若地图中某个五邻国构形区域可着4色(包含中心、及周围共6个国家),则该五邻国构形周围的5个国家只能着3色(下文简称“5邻3色”),共有5种等价形态(如下图3色:A、B、C)。

当构形周围5个国家以指定顺序着3色时(A、B、C),可以轻易构造出必须使用5种颜色的地图:
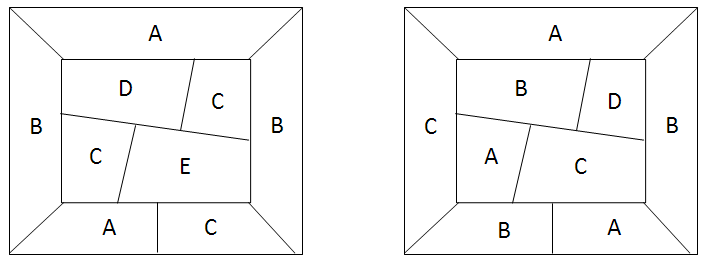
但调整构形周围5个国家的着色顺序(仍为A、B、C三种颜色),我们发现地图上国家间的邻接关系会破坏消减,调整后的地图用4种颜色即可完成着色。
这种“东方不亮西方亮、黑了南方有北方”的现象,在构形周围5个国家以指定顺序着4色时也同样存在(不考虑对构形中心的国家着色,下文简称“5邻4色”):
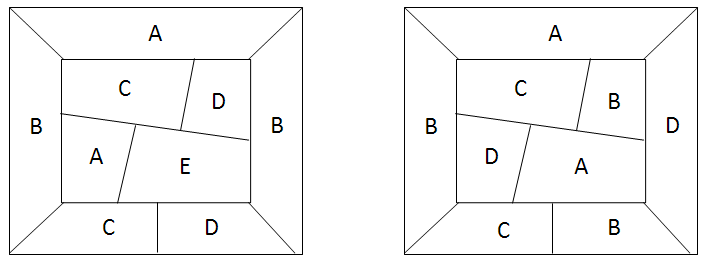
可能性说明:地图局部五邻国构形以外国家数量超过4个、且构形指定“5邻3色”时,可能无法构造出有5个两两相邻国家的地图,若能证明此点,也能证明五邻国构形可约。本文未对此可能点深入分析。
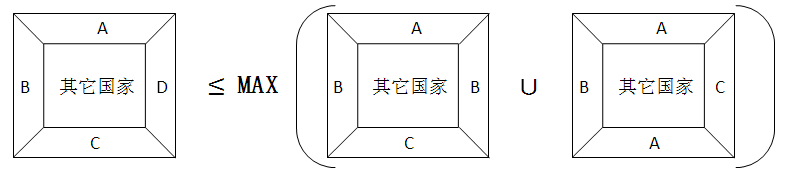
根据五色定理,对于任意平面地图上的局部五邻国构形,在不考虑对构形中心的国家着色时,该构形周围的5个邻国,一定可以着4色。因为构形周围“5邻4色”共有5种等价组合,这5种等价地图中,至少有3种地图存在四色足够的着色方案:

推证:我们知道四邻国构形一定可约,四邻国构形周围的4个国家也一定可以着3色(不考虑构形中心国家)。因为构形周围“4邻3色”共有2种等价组合,那么这两种等价组合中,至少有1种地图是四色足够的。
而构形周围“5邻4色”的5种等价地图中,互相存在交叉斥补关系。根据“4邻3色”2种等价组合中必有1种地图四色足够推断,“5邻4色”的5种等价地图中一定存在不少于5/2,即>=3种地图是四色足够的。
如需证明包含五邻国构形的地图可着4色,则构形周围“5邻3色”的5种等价地图中,至少要存在1种地图是四色足够的。
也即:如果任意地图局部五邻国构形“5邻3色”的5种等价组合中,至少存在1种地图是四色足够的,则五邻国构形一定可约。
下面求解任意五邻国构形“5邻3色”的5种等价地图中,最少的着色数量:

因四邻国构形一定可约,我们从四邻国构形的各种演变入手,分析构形周围各种着色组合的地图最少着色数量:
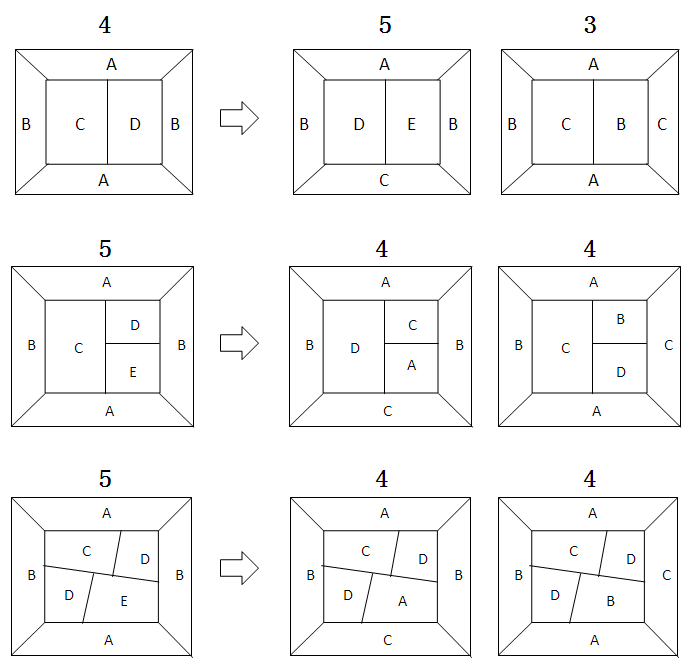
如上图所示,当构形周围4个国家着2色(下文简称“4邻2色”)时,原始地图同演变地图的最少着色数量似乎没有规律;
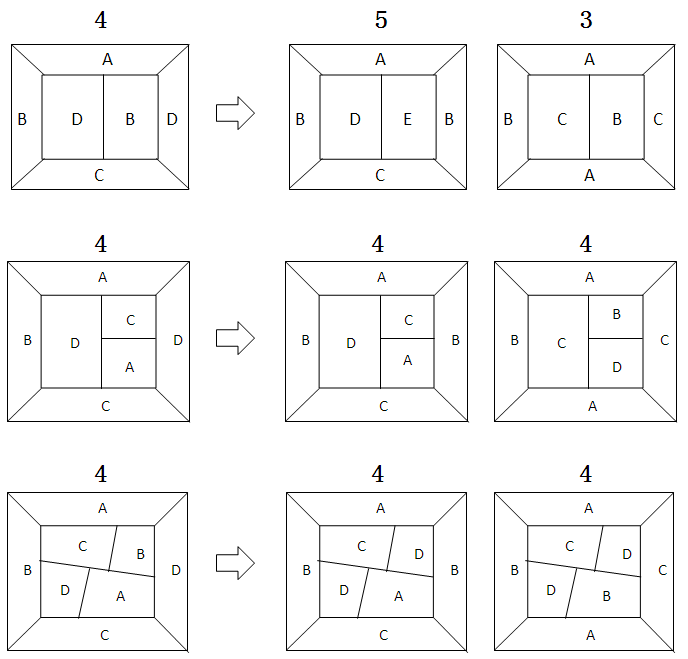
如上图所示,而当构形周围4个国家着4色时(不考虑对构形中心国家着色,下文简称“4邻4色”),原始地图同演变地图的最少着色数量存在以下规律:
构形周围“4邻2色”时,原始地图同演变地图的最少着色数量不连续,分析是因为构形区域之外存在1个或几个国家,这些国家同构形周围不相邻的国家间均不存在肯普链,且被限制不能复用不相邻国家的着色;
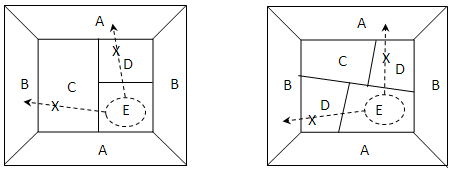
针对构形周围“5邻3色”的五邻国构形,构形区域之外不会存在类似情况,如果某个国家同构形周围不相邻的国家均无肯普链,则一定可以构建出肯普链、或者可与某个构形周围不相邻的国家着同色。
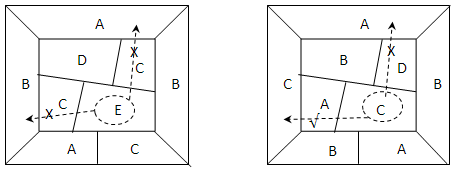
因此构形周围“5邻3色”,演变为“5邻4色”,原始地图同演变地图的最少着色数量是连续的,有以下推断:
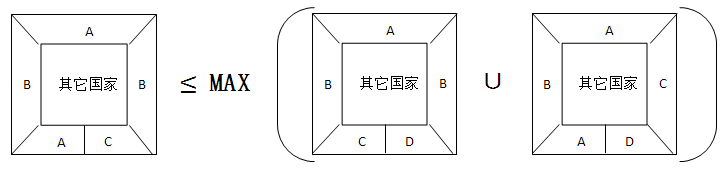
构形周围“5邻3色”的5种等价地图,与“5邻4色”的5种等价地图之间的演变关系如下:
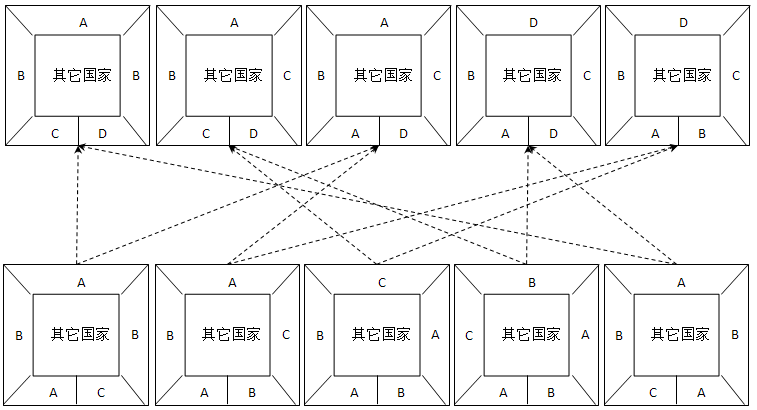
从上文推断,我们知道构形周围“5邻4色”的5种等价地图中,一定有3种地图是四色足够的。
根据鸽巢原理,3种四色足够的“5邻4色”地图中,一定有2种是由同一个“5邻3色”地图演变而来,而该“5邻3色”地图也一定是四色足够的。
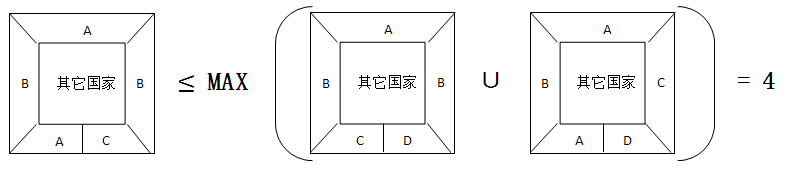
如此我们得到了预期的结果:构形周围“5邻3色”的5种等价地图中,一定存在至少1种地图是四色足够的。

从而推得任意地图中的局部五邻国构形可约,四色定理得证。
四、参考
https://zh.wikipedia.org/wiki/四色定理
https://baike.baidu.com/item/四色定理
https://baike.baidu.com/item/七色定理
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享




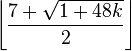 种颜色就能为任意的地图染色,其中k是曲面的亏格。当k=0的时候,这个猜想就变成了四色猜想。当地图中存在“飞地”时(地图中某两个不相邻的地区属于同一个国家,必须着同色),有K≥1。在1968年,杰拉德.格尔和J.W.T.杨格斯最终证明了这个猜想在k≥1时的情况。
种颜色就能为任意的地图染色,其中k是曲面的亏格。当k=0的时候,这个猜想就变成了四色猜想。当地图中存在“飞地”时(地图中某两个不相邻的地区属于同一个国家,必须着同色),有K≥1。在1968年,杰拉德.格尔和J.W.T.杨格斯最终证明了这个猜想在k≥1时的情况。













