《数据结构与算法》知识小结

[依然～]

数据结构在研究的其实就是逻辑结构，其中包括线性结构、树结构、图结构。
线性结构：结构中的数据元素之间存在着一对一的线性关系。
树结构：结构中的数据元素之间存在着一对多的层次关系。
图结构：结构中的数据元素之间存在着多对多的任意关系。
算法是对特定问题求解步骤的一种概述，它是指令的有限序列，其中每一条指令表示一个或多个动作。
算法的特性：有穷性、确定性、可行性、输入、输出。
算法设计需要满足的要求：正确性、可读性、健壮性、效率与低储存量需求。
以上是对数据结构和算法一个简单的介绍，下面就是围绕数据结构与算法学习的一些知识。

1线性表：
线性表中讲到了顺序表和单链表，还分别讲了它们的插入和删除。
顺序表的插入特点就是你要插入哪个位置，它就会从最后一个元素开始往后移，直到空出要插入的位置。删除的话就把删除的位置的元素移出，紧接着后面的每一个元素都会往前移一位。单链表插入的特点就是定位在插入位置的前一位然后插入。删除的话就简单了，直接删除那个位置的元素。

2堆栈和队列：
堆栈的特点就很明显了，后进先出。
栈的基本运算有：初始化堆栈、判定栈S是否为空、求堆栈S 的长度、获取栈顶元素的值、将元素e进栈还有出栈。
栈的存储结构：顺序栈、链栈
队列又简称队，其中插入又叫做入队，删除叫做出队。队列的存储结构也是顺序队列和链式队列。
在插入队列的时候如果队列为满就会查询溢出。解决这个问题就是用循环队列。
循环队列为满的条件是：front==( rear+1) % MaxSize

3字符串：
串是由零个或多个字符组成的有限序列，记作s=”s0s1…sn-1”(n≥0)，其中s是串名，字符个数n称作串的长度，双撇号括起来的字符序列”s0s1…sn-1”是串的值。每个字符可以是字母、数字或任何其它的符号。零个字符的串（即：””）称为空串，空串不包含任何字符。值得注意的是：
（1）长度为1的空格串" "不等同于空串""；
（2）值为单个字符的字符串不等同于单个字符，如"a"与′a′；
（3）串值不包含双撇号，双撇号是串的定界符。

4数组与矩阵：
数组其实就是有序的元素序列，数组在Java语言中有很多功能：分配存储空间、获得数组长度、存数组元素、取数组元素。数组包括一维数组、二维数组、三维数组、四维数组等等。
如何理解数组呢？一维数组中每一个元素都是一维数组，那二维数组也就是两个元素在一块，三维数组呢，就可以把二维数组比作是一页纸，那三维数组就是一本书。以此类推，四维数组就是放书的书架、五维数组就是图书馆了。
矩阵在数学中是一个按照长方阵列排列的复数或实数的集合。矩阵在生活中一般应用到图像处理、信息加密等等。还有一些特殊的矩阵，零矩阵、方阵、对角矩阵、单位矩阵、上/下三角形矩阵和行/列矩阵。

5树：
树大家看到都知道是很有层次的，树根、树枝、树叶。这就好像一个公司中的总经理、部门经理、员工。树形结构是一种应用十分广泛的非线性结构，客观世界中广泛存在。那么在计算机中如何表示树呢。定义是这样的，树是由n(n≥0)个结点组成的有限集合。如果n=0，那就叫做空树。如果n>0，则满足：
有一个特定的称之为根(root)的结点，它只有直接后继，但没有直接前驱；
除根以为的其他结点划分为m(m>0)个互不相交的有限集合T1，T2，T3……Tm,每个集合又是一棵树，并称为根的子树。（每棵子树的根结点有且仅有一个直接前驱，但它可以有0个或多个直接后继）
下面还有树的一些基本术语：节点、节点的度、树的度、叶子、分支、孩子、双亲、兄弟、有序树和无序树、森林、树的深度。这些基本术语可以让我们学习树的时候更方便快速的理解和记忆。
还有一种特殊的树，符合二孩政策的树—二叉树；二叉树是n(n≥0)个结点组成的有限集合BT，它或者是空集、或者由一个根节点和两颗分别称为左子树和右子树的互不相交的二叉树组成。
二叉树的遍历也有几种方法：先根遍历（TLR）、中根遍历（LTR）、后根遍历（LRT）;
二叉树的链式存储结构，最常用的就是二叉链表和三叉链表。还有就是二叉树的创建，如下图所示：

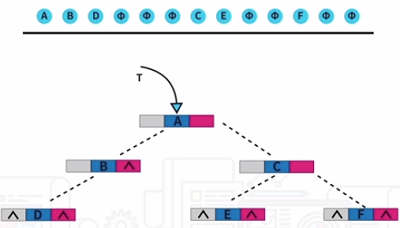
还有一种称为最优二叉树的：哈夫曼树
哈夫曼树的基本概念有路径长度和树的路径长度
结点的带权路径长度:从根结点到某个结点的路径长度与该结点所带的权值的乘积。
树的带权路径长度就是所以叶子结点的带权路径长度之和。通常记作如下图所示：


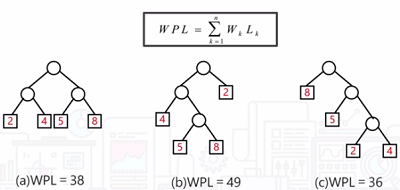
构造哈夫曼树的方法如下图所示：


6图：
在实际应用中，有很多可以用图结构来描述的问题，比如旅游路线可以用图画出来，而我们学习的这个图就可以帮助我们用最少的资金和时间来规划一个好的旅游方案。
 图是由顶点和边组成的，定点表示图中的数据元素，边表示数据元素之间的关系记为G=(V,E)，其中V是顶点的非空有穷集合，E是用顶点对表示的边的有穷集合, 可以为空。
图的基本术语：邻接点、顶点的度、入度和出度、完全图、稠密图、稀疏图、子图、路径、连通图、连通分量、强连通图、强连通分量、权、网。
图的存储结构：邻接矩阵和邻接表。
 图的遍历：从中某一顶点出发遍历图中其余顶点，且使每一顶点仅被访问一次。
算法设计需要注意的几个问题：1、算法的参数要指定访问的第一个顶点；2、要考虑遍历路径可能出现的死循环问题；3、要使每一个顶点的所有邻接顶点按照某种次序被访问。
遍历图的基本方法：深度优先搜索和广度优先搜索。
下面看看连通图的深度优先搜索遍历DFS和一个示例，如下图所示：


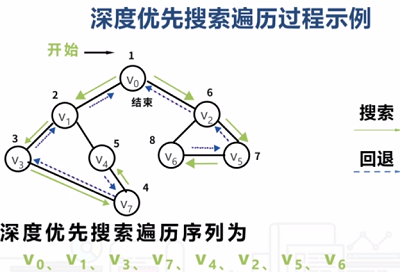
解决图的最短路径问题的方法：Dijkstra算法和Floyd算法。
Dijkstra算法：按路径长度的递增次序，逐步产生最短路径的算法。首先求出长度最短的一条最短路径，再参照它求出长度次短的一条最短路径，依此类推，直到顶点V到其它各顶点的最短路径求出为止。下面看一个示例，如下图所示：



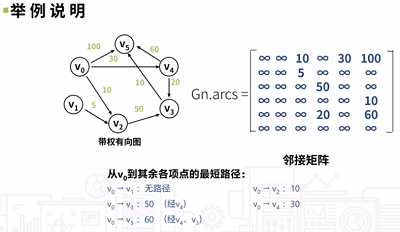
7查找：
查找分为静态查找、动态查找和哈希查找，下面我们就一个一个看。
 静态查找又包括：顺序查找、折半查找、分块检索。
顺序查找：查找表的存储结构是线性表；查找过程是依次用查找条件中给定的值与查找表中数据元素的关键字值比较。
下面我们看一下顺序查找的完整算法，如下图所示：

折半查找：折半查找只适用于对有序顺序表进行查找；每进行一次折半查找，要么查找成功，结束查找；要么将查找范围缩小一半，继续查找；如此重复，直到查找成功或查找范围缩小为空即查找失败为止。折半查找又称二分查找。
分块检索：分块检索又称索引顺序查找，它是一种性能介于顺序查找和二分查找之间的查找方法。查找表由 ‘分块有序’ 的线性表和 ‘有序的‘ 索引表组成。

 动态查找：表结构本身是在查找中动态生成，对于给定值K，如果表中存在则查找成功，否则在适当位置插入K。它的结构主要有二叉树结构和树结构两种类型。
二叉排序树又称二叉查找树，它或者是空树，或者是满足以下性质：1、若它左子树非空，则左子树上所有结点的均小于根结点的值；2、若它右子树非空，则右子树上所有结点的均小于根结点的值；3、它的左、右子树本身又各是一棵二叉排序树。
在二叉排序树中查找的基本思想：用给定K值与根节点关键字值比较，如果K小于根节点的值，就继续在左子树中查找，否则将继续在右子树中查找，依此类推，一直查找下去，直到查找成功或者查找失败为止。
下面看一个完整的二叉排序树查找算法，如下图所示：



哈希查找，简单的介绍，如下图所示：

哈希查找中的方法，如下图所示:：


8排序：
排序也分为几种：插入排序、交换排序和选择排序。
 插入排序：开始时有序表中只包含一个元素，无序表中包含n-1个元素；排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表；每一趟都是将一个记录插入到前面的有序段中，直到所有记录都插入到有序段中，需要进行n-1趟。
注意：直接插入算法的元素移动是顺序的，该方法是稳定的。
直接插入排序适用于对排序元素较少、且基本有序的数据元素排序。
直接插入排序算法描述如下图所示：

 交换排序：又叫做快速排序，基本思想就是从待排序序列的n个记录中任取一个记录R,作为基准记录，以基准记录为界限，将待排序序列划分成两个子序列，所以关键字小于Ki的记录移动到Ri前面，反之，移动到后面，这个过程称做一趟快速排序，然后用同样的方法对两个子序列排序，得到四个子序列；依次类推，直到每个子序列只有一个
记录为止，此时就得到n个记录的有序序列。
快速排序算法描述和快速排序的递归算法如下图所示：

 选择排序：基本思想就是每一趟从待排序记录中选出关键字最小的记录，按顺序放到已排好序的子序列中，直到全部记录排序完毕。选择排序有两种：直接选择排序和堆排序。

直接选择排序算法描述如下图所示：

在直接选择排序过程中，所需移动记录的次数较少。在最好情况下，即待排序序列正序时，该算法记录移动次数为0，反之待排序序列逆序时，该算法记录移动次数为（n-1）。
在直接选择排序过程中需要的关键字的比较次数与序列原始顺序无关，大概i=1时（外循环执行第一次），内循环比较n-1次，i=2时，内循环比较n-2次；依次类推，算法的总比较次数为(1+2+3+…+n-1) = n(n-1)/2。因此直接选择排序的时间复杂度为O(n²)，由于只用一个变量作辅助空间，所以空间复杂度为O(1)，直接选择排序是不稳定的。

以上就是数据结构与算法的小总结，大家可以参考或学习。