176
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享
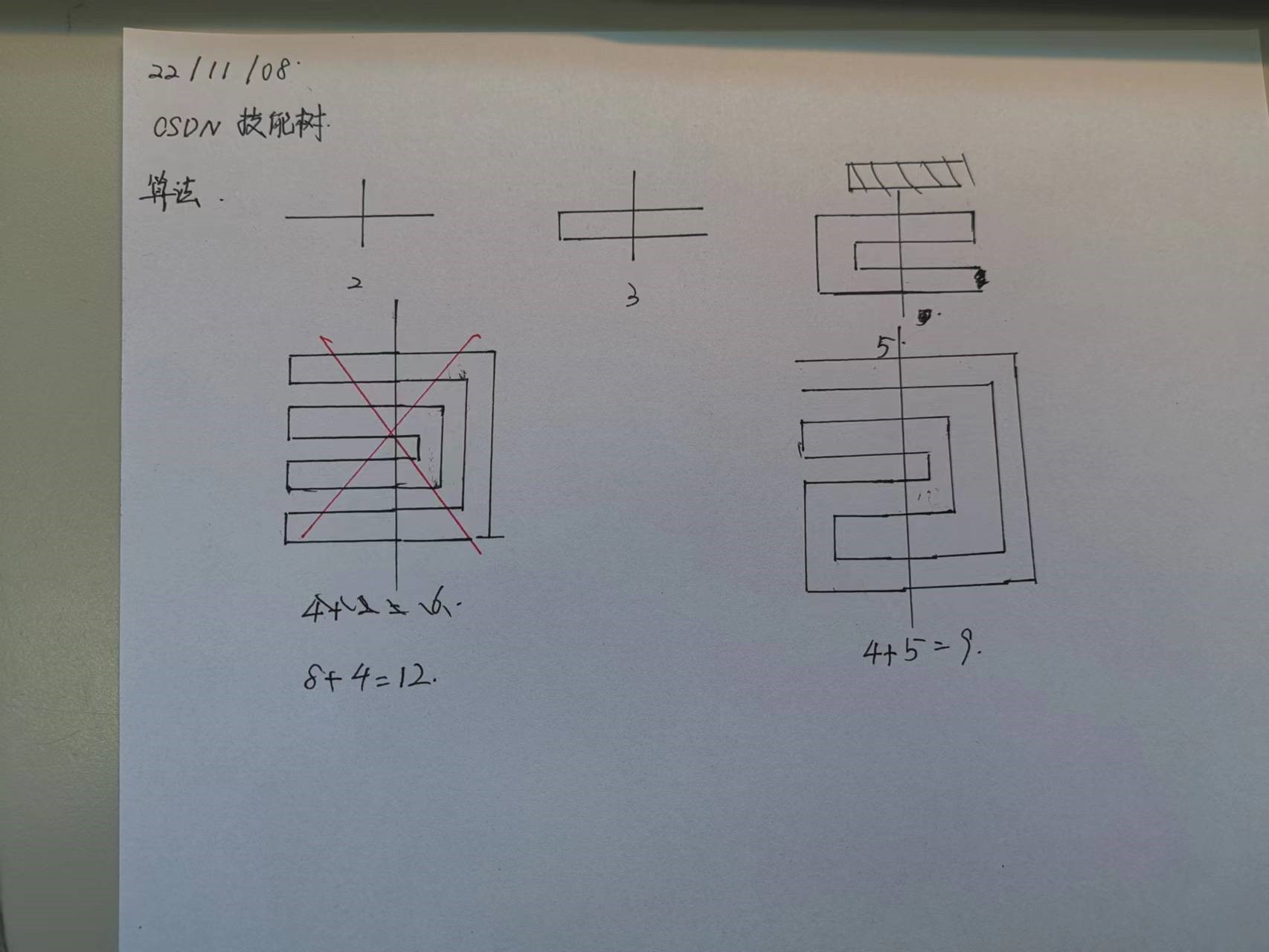
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。 那么,连续对折10次,中间切一刀,会得到多少面条呢?
切面条
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。 那么,连续对折10次,中间切一刀,会得到多少面条呢?
如图所示:折叠一次两次三次的图像均已画出。出去不折叠这个特殊情况之外,可以分析规律得出公式:x = 2^k + 1 (x是面条条数,k是对折次数)。故答案为:2^10 + 1 =1025
连续对折三次,中间切一刀,会得到多少面条呢?不难知道,答案是9条(如果不能画图得出,可以用一张长条连续对折三次从中间撕开)。经过归纳,不难发现面条数N与对折次数n满足这样的关系:N = 2^n+1。
一根面条,中间切一刀,会变成两根面条,所以对于本题,可以有定义1:
中间切一刀,会变成两根的叫面条。
将一根面条不对折,中间切一刀,会变成两根面条;如果将一根面条收尾相连变成一个环,切一刀,也是变成两根面条:也就是说二者的面条数相等。既然二者产生的结果相同,所以可以将二者等效。根据定义1,可以将一个环看成是一根面条,且从宏观上看,多次对折的面条变成的环也可以看成是一根面条。又有将一根面条对折一次,中间切一刀,会变成三根面条,对于本题,可以有定理1:
对折切的结果是产生一根新的面条,且面条数少一。
N|n=0 = 2。根据定理1,N|n=1 = 2^1+1 = 3,N|n=2 = 2^2+1 = 5,...,N = 2^n+1。
为什么不是N = ((((2^1+1)^2+1)^3+1)...^n+1)。在正在对折的过程中,仍处在等效的状态当中,环未拆开即首位未断开,直到形成最终的一根面条中间切后将首尾断开才把少的面条数加上去。
假设每折一次面条整体分两半(此时假设面条是脆的),那么折n次时面条总个数为2^n,再在中间切一刀时面条又加倍,此时为2^(n+1)段;实际情况是面条折叠是中间有牵连,当我们折n次时(假设每次都是从有连接的那端向分叉的那端折,这样便于想象),将软面条两端各切一刀就与脆面条折叠后结果相等,即软面条是2^(n+1)/2+1=2^n+1
可以这样想,一根面条不对折切一刀就是一刀,对折一次之后,切一刀不久相当于切两刀吗,对折两次之后,切一刀就相当于切四刀,四刀五五段,对折十次切一刀就是2的十次方刀,相当于2的十次方+1段
int qiemian(int n)
{
int count = 2;
if (n == 0);
else
{
count = qiemian(n - 1) + pow(2, n - 1);
}
return count;
}
此内容由Chat GPT 3.5提供:根据描述,可以得出结论如下:连续对折10次,中间切一刀,最终会得到 2^10 * 1 = 1024 根面条。
public static void main(String[] args) {
int folds = 10;
int noodles =(int)Math.pow(2, folds)+1;
System.out.println(noodles);
}
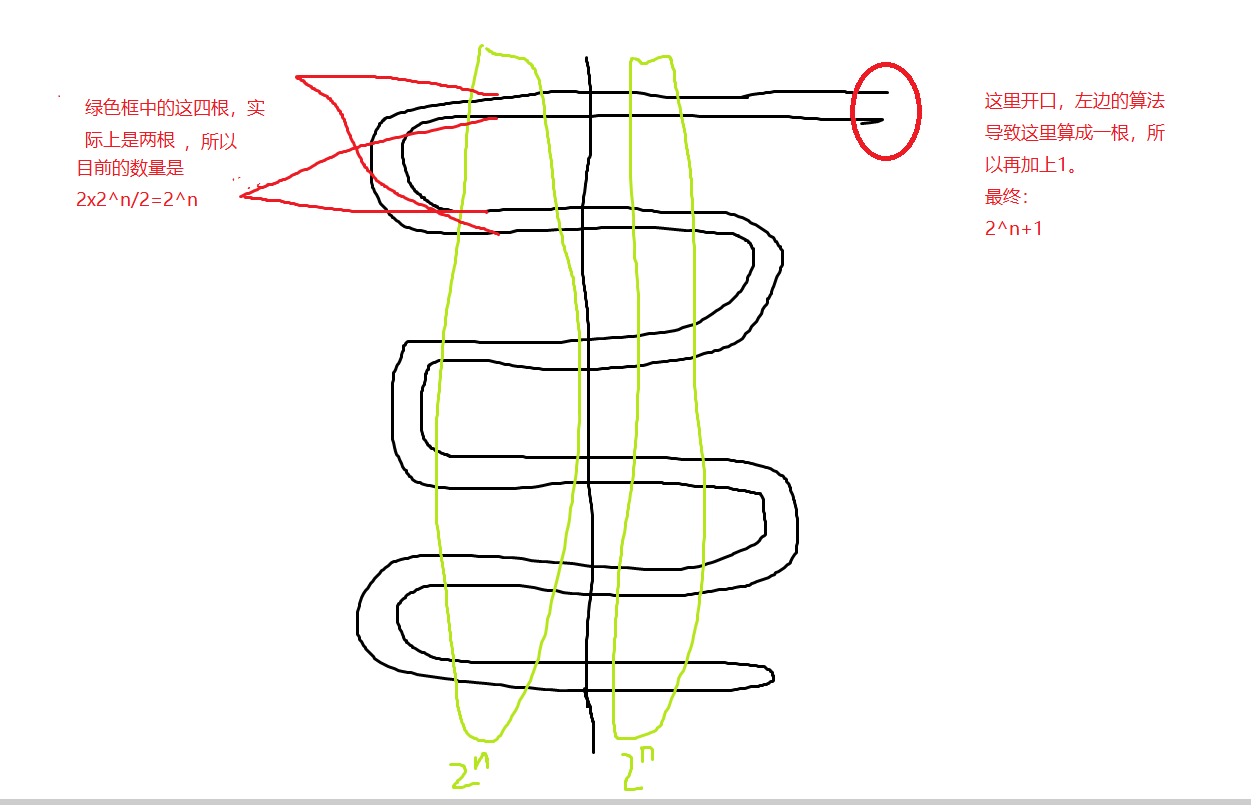
一根面条对折n次切一刀,如果不考虑对折点,答案是22^n。 实际情况下,每个对折点只有一根。所以需要减去对折点的个数。
对折点个数跟次数的关系是2^1+......+2^n,等比数列求和结果是2^n -1。
所以最终结果等于不考虑对折点减去对折点个数=22^n -(2^n -1) ,简化后=2^n+1
#include <stdio.h>
int main()
{
int n, shu[2];
shu[0] = 0;
scanf("%d", &n); //对折n次
while (n--) {
shu[1] = shu[0] * 2 + 1; //不为两边部分的数量为上一次的两倍加一
shu[0] = shu[1];
}
printf("%d", shu[1] + 2); //2为面的两头
return 0;
}
一根面条,
对折0次,0个拐角,切一刀出现2根面条
对折1次,1个拐角,切一刀出现4-1根面条(切之前的面条层数*2-拐角数)
对折2次,1+2个拐角,(原有拐角(此处为1)+上一次对折结束后面条的层数(此处为2)),切一刀出现8-(1+2)根面条
对折n次,1+2+4+..+2^(n-1)个拐角,切一刀出现2^n-(1+2+4+...+2^(n-1))根面条
将10带入,得到2^10-(1+2+4+...+2^(10-1))=2048-1023=1025