你说的都对-第二十一天-在的-第九章知识点全

[羡鱼数与模]

第九章：

接着上面的拉普拉斯微分方程应用：

学过复变的可以知道，这就是当初学习微分方程时候所讲的章节 

我们用例题来阐述它叭：

 我们利用所学的复变知识，可以将两边先拉普拉斯变换一下变为：

整理最终得到：

 

而Y（t)是单位跃阶函数，在复变当中定义为：

 

我们可以先看看他的图是长什么样的：

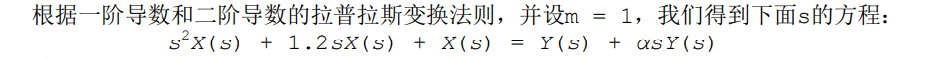
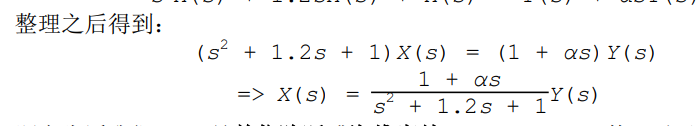
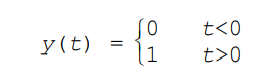
syms t
eq = heaviside(t);
ezplot(eq,[-2,2]);

 

接下来对其进行laplace变换：

 

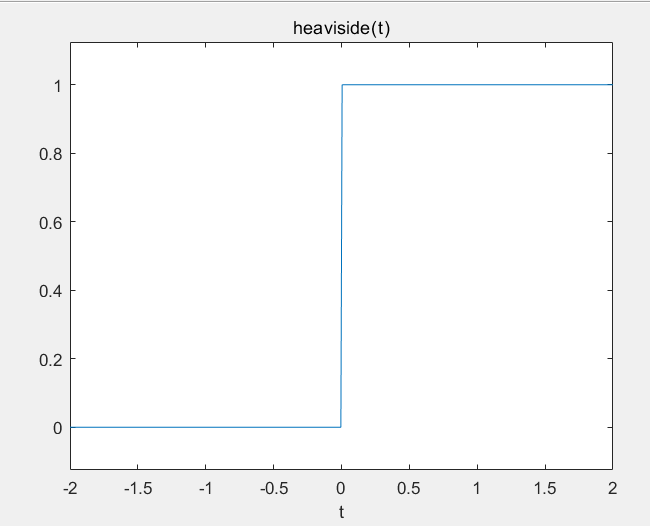
s = laplace(eq)

注意我设的s和其中的s不是一个东西

 

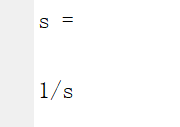
%我们将所取值全部分开
a = 2; b = 2; c = 5;
syms s
d = s^2 + 1.2*s + 1;
Xa = ((1+ a*s)/d)*(1/s)
Xb = ((1+ b*s)/d)*(1/s)
Xc = ((1+ c*s)/d)*(1/s)

 xa = ilaplace(Xa)
 xb = ilaplace(Xb)
 xc = ilaplace(Xc)

可以看到，解微分方程无非就是先拉普拉斯变换，再拉普拉斯逆变换就好了。

 接下来我们来看傅里叶变换，它可以说是拉普拉斯变换的来源，毕竟拉普拉斯变换是因为降低满足要求而创造出来的，而傅里叶变换的满足条件更加严苛，所以在工程上很难得到应用罢了。

先来一个简单的小例子：

 你还记得dirac函数是什么嘛？

来，我们来画个图增长印象叭：

在复变当中，他是上面所说的单位跃阶函数的导数！他自己称为单位脉冲函数，其实他也有不等于0的地方，只是没有展现 

 我们继续来看看它的伟大作用，比如，将一个尖端变成一个好看的波形：

我们先来看看这个函数的图像：

 

再来看看傅里叶变换之后的图像：

 

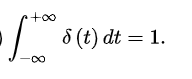
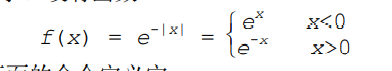
syms x;
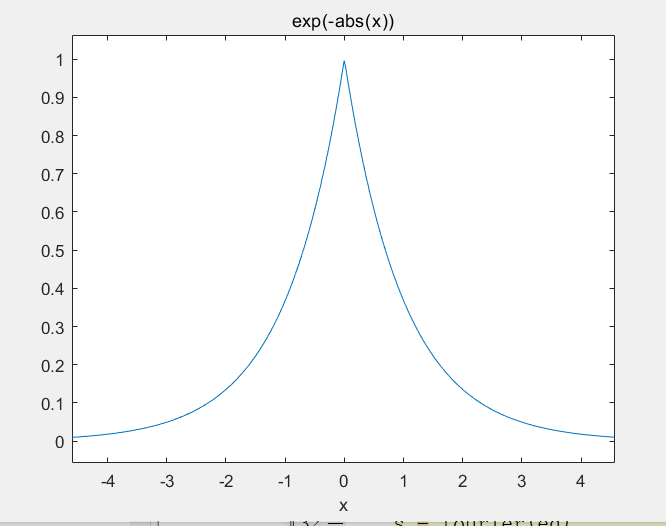
f = exp(-abs(x));
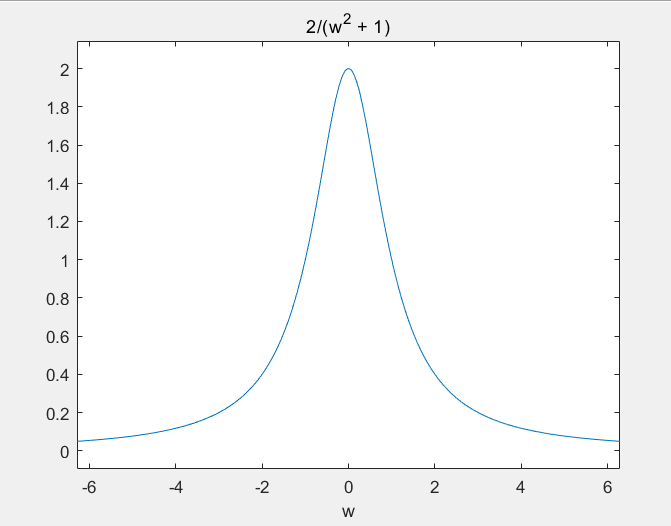
FT = fourier(f) ;
ezplot(f)
ezplot(FT)

是不是很奇妙？ 这就是它的一个作用之一，创一个波形函数。

接下来我们来看看快速傅里叶变换：

是用来计算数值向量的：

我们搭配例题来使用它：

我们首先先画出这样一个信号吧？

 

 

syms x(t)
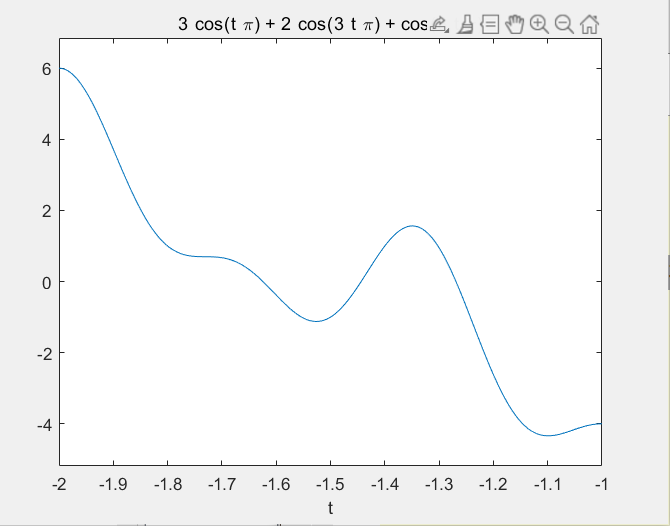
x = 3*cos(pi*t) + 2*cos(3*pi*t) + cos(6*pi*t);

ezplot(x,[-2 -1]);

接下来建立噪声模型叭？时间给了，是十秒，那么给这十秒分段吧，区间隔0.1：

建立噪声的时候用随机函数：

t = 0:0.01:10
x = 3*cos(pi*t) + 2*cos(3*pi*t) + cos(6*pi*t);
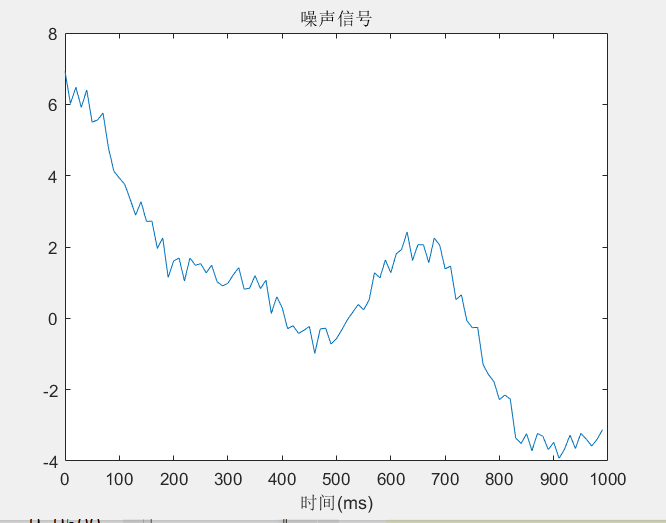
x_noise = x + rand(size(t));
plot(1000*t(1:100),x(1:100)), xlabel('时间(ms)'), title('原始信号')
plot(1000*t(1:100),x_noise(1:100)),xlabel('时间(ms)'), title('噪声信号')

 

最终提取有效信息：

 

 

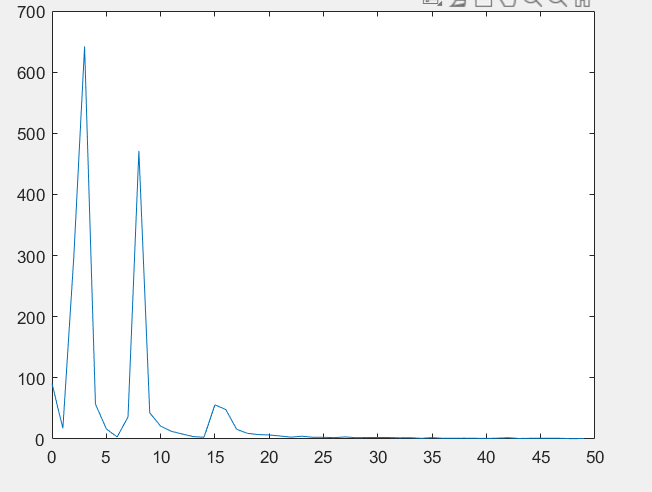
FT = fft(x_noise,512);
P = FT.*conj(FT)/512;
 f=t/0.01
 plot(f(1:50),P(1:50));

关于傅里叶变换其实这里有很多没有讲清楚，本人自己也暂时没有能力讲，所以还请读者有兴趣的话自行寻找想要知道的答案

[CSDN-Ada助手]

您可以前往 CSDN问答-非IT技术 发布问题, 以便更快地解决您的疑问