求助大佬matlab离散点如何求曲率

[weixin_45310257]

在abaqus有限元后导出的二维数据如何在matlab中求其曲率（不拟合曲线的情况下）

[CSDN-Ada助手]

您可以前往 CSDN问答-编程语言 发布问题, 以便更快地解决您的疑问

[海棠AI实验室]

在MATLAB中，给定离散的二维数据点，可以通过数值方法来计算曲率。曲率是描述曲线弯曲程度的一个量，通常可以通过对曲线的二阶导数进行计算来求得。对于离散的点集，曲率可以通过数值微分的方法来近似计算。

1. 离散数据点的曲率计算原理

曲率的计算公式是：

其中，x', y' 表示曲线在 x 和 y 方向上的一阶导数，x'', y'' 表示曲线在 x 和 y 方向上的二阶导数。

对于离散的点集，无法直接求导数，因此可以通过数值微分方法（如中心差分法）来估算一阶和二阶导数。

2. 求导数的数值方法

一阶导数（速度）：

二阶导数（加速度）：

二阶导数可以通过类似的方式计算：

3. MATLAB中的实现步骤

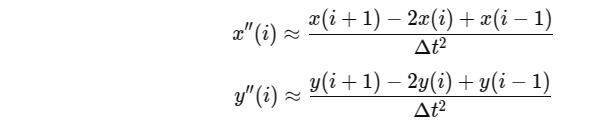
假设我们已经从Abaqus导出了二维数据，数据格式为一个包含离散点的数组，每一行包含一个点的 (x) 和 (y) 坐标。可以按照以下步骤计算曲率：

3.1 载入数据

假设导出的数据存储在名为 data 的变量中，data(:, 1) 为 (x) 坐标，data(:, 2) 为 (y) 坐标。

% 假设数据已经被载入，data 是二维数据矩阵，每行表示一个点
x = data(:, 1);  % x坐标
y = data(:, 2);  % y坐标
n = length(x);   % 点的数量

3.2 计算一阶导数（速度）

使用中心差分法来计算一阶导数。

dx = diff(x);    % x的差分
dy = diff(y);    % y的差分

% 计算速度
vx = [0; (x(3:end) - x(1:end-2)) / 2];  % 一阶导数：中心差分
vy = [0; (y(3:end) - y(1:end-2)) / 2];  % 一阶导数：中心差分

3.3 计算二阶导数（加速度）

同样使用中心差分法计算二阶导数。

% 计算加速度
ax = [0; diff(x, 2)];  % 二阶导数：中心差分
ay = [0; diff(y, 2)];  % 二阶导数：中心差分

3.4 计算曲率

有了速度和加速度，我们可以通过曲率公式来计算每个点的曲率。

% 计算曲率
numerator = vx(2:end) .* ay(2:end) - vy(2:end) .* ax(2:end);
denominator = (vx(2:end).^2 + vy(2:end).^2).^(3/2);
curvature = numerator ./ denominator;

% 为了对齐索引，添加前后零值
curvature = [0; curvature; 0];

3.5 绘图和可视化（可选）

% 绘制原始点和曲率
figure;
subplot(1,2,1);
plot(x, y, '-o');  % 绘制原始点
title('Original Data');
xlabel('x');
ylabel('y');

subplot(1,2,2);
plot(1:n, curvature, '-o');  % 绘制曲率
title('Curvature');
xlabel('Point Index');
ylabel('Curvature');

4. 注意事项

• 边界条件：由于差分法的计算需要相邻的两个点，因此第一个和最后一个点的导数计算可能不准确，常常需要手动处理边界点（如使用前向差分或后向差分）。

• 数据预处理：在实际使用中，Abaqus 导出的数据可能包含噪声或不规则间隔的点，因此在计算曲率之前，可能需要对数据进行平滑或插值。

• 曲率的单位：曲率的单位是“1/长度”，如果坐标单位为米，曲率的单位则是“1/米”。

5. 总结

在MATLAB中，通过数值微分可以有效地计算离散点的曲率，而不需要拟合曲线。通过使用中心差分法计算一阶和二阶导数，然后通过公式计算曲率，最终可以得到每个数据点的曲率值。