84
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享爸爸
人呢
import sys
from PyQt5.QtWidgets import QApplication,QWidget
import buttonClick
class QmyWidget(QWidget):
def __init__(self,parent = None):
super().__init__(parent)
self.ui = buttonClick.Ui_Form()
self.ui.setupUi(self)
self.ui.pushButton.clicked.connect(self.clickedBtn)
self.ui.pushButton_2.pressed.connect(self.pressedBtn)
self.ui.pushButton_3.released.connect(self.releasedBtn)
self.ui.pushButton_4.toggled.connect(self.toggleBtn)
def clickedBtn(self):
self.ui.textEdit.append('按钮Clickbtn被点击')
def pressedBtn(self):
self.ui.textEdit.append('按钮PressBtn被按下')
def releasedBtn(self):
self.ui.textEdit.append('按钮ReleaseBtn被释放')
def toggleBtn(self,status):
self.ui.textEdit.append(f'按钮Toggglebtn被选中:{status}')
if __name__ == '__main__':
app = QApplication(sys.argv)
myWindow = QmyWidget()
myWindow.show()
n = app.exec()
sys.exit(n)
import numpy as np
import matplotlib.pyplot as plt
def process_features(X):
m, n = X.shape # 求X矩阵的行数和列数
X = np.c_[np.ones((m, 1)), X] # 将m行1列的矩阵与X拼接
return X
def fit(X, y): # 求正规方程
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y) # w*=(XT⦁X)-1⦁X⦁y
return w
def predict(X,y): # 预测X对应的Y值
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
return X.dot(w) # Y_pred = X ⦁ w*
def mean_squared_error(y_true, y_pred): # 求均方误差
return np.average((y_true - y_pred) ** 2, axis=0)
def r2_score(y_true, y_pred): # 求决定系数
numerator = (y_true - y_pred) ** 2
denominator = (y_true - np.average(y_true, axis=0)) ** 2
return 1 - numerator.sum(axis=0) / denominator.sum(axis=0)
dots = np.array([[0, 5],[1, 6.5],[2, 9.5],[3, 11],[4, 12],[5, 14]]) # 点坐标
X = dots[:, [0]] # 取出每个坐标X轴的值
Y = dots[:, [1]] # 取出每个坐标Y轴的值
X_1 = process_features(X) # 首位置1
theta = fit(X_1, Y) # 求解正规方程
Y_pred = predict(X_1,Y) # 求解X的预测值
mse = mean_squared_error(Y, Y_pred) # 求均方误差
r2 = r2_score(Y, Y_pred) # 求决定系数
print("theta:{}".format(theta))
print("mse = {}".format(mse))
print("r2 = {}".format(r2))
plt.figure()
plt.title("Scatter Fitting")
plt.plot(X, Y, "bs", ms=3) # 画散点
plt.plot(X, Y_pred, color='red') # 打印直线
plt.show()
theta:[[0.86666667]
[2. ]]
mse = [0.00888889]
r2 = [0.99667774]
import numpy as np
import matplotlib.pyplot as plt
def process_features(X):
m, n = X.shape # 求X矩阵的行数和列数
X = np.c_[np.ones((m, 1)), X] # 将m行1列的矩阵与X拼接
return X
def fit(X, y): # 求正规方程
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y) # w*=(XT⦁X)-1⦁X⦁y
return w
def predict(X,y): # 预测X对应的Y值
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
return X.dot(w) # Y_pred = X ⦁ w*
def mean_squared_error(y_true, y_pred): # 求均方误差
return np.average((y_true - y_pred) ** 2, axis=0)
def r2_score(y_true, y_pred): # 求决定系数
numerator = (y_true - y_pred) ** 2
denominator = (y_true - np.average(y_true, axis=0)) ** 2
return 1 - numerator.sum(axis=0) / denominator.sum(axis=0)
dots = np.array([[0, 5],[1, 6.5],[2, 9.5],[3, 11],[4, 12],[5, 14]]) # 点坐标
X = dots[:, [0]] # 取出每个坐标X轴的值
Y = dots[:, [1]] # 取出每个坐标Y轴的值
X_1 = process_features(X) # 首位置1
theta = fit(X_1, Y) # 求解正规方程
Y_pred = predict(X_1,Y) # 求解X的预测值
mse = mean_squared_error(Y, Y_pred) # 求均方误差
r2 = r2_score(Y, Y_pred) # 求决定系数
print("theta:{}".format(theta))
print("mse = {}".format(mse))
print("r2 = {}".format(r2))
plt.figure()
plt.title("Scatter Fitting")
plt.plot(X, Y, "bs", ms=3) # 画散点
plt.plot(X, Y_pred, color='red') # 打印直线
plt.show()
theta:[[0.86666667]
[2. ]]
mse = [0.00888889]
r2 = [0.99667774]
有无第三题 h 答案
有无第一题



决策树模型在机器学习基础与实战页码p190

import matplotlib.pyplot as plt
import numpy as np
from svm_smo import SVM
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X = np.array([[0, 1], [1, 0.5], [2, 2], [3, 1], [0.5, -2], [1.5, -1.5], [2.5, -2.5], [3.5, -2]])
y = np.array([1, 1, 1, 1, -1, -1, -1, -1]).reshape(-1, 1)
model = SVM()
model.fit(X, y, N=10)
plt.subplot(1, 1, 1)
plt.axis([-5, 10, -5, 5])
plt.scatter(X[:, 0][y[:, 0] == 1], X[:, 1][y[:, 0] == 1])
plt.scatter(X[:, 0][y[:, 0] == -1], X[:, 1][y[:, 0] == -1])
x0 = np.linspace(-10, 15, 200)
line = -model.w[0] / model.w[1] * x0 - model.b / model.w[1]
plt.text(5, 7, 'y = -model.w[0]/ model.w[1]*x0-model.b/model.w[1]')
plt.plot(x0, line)
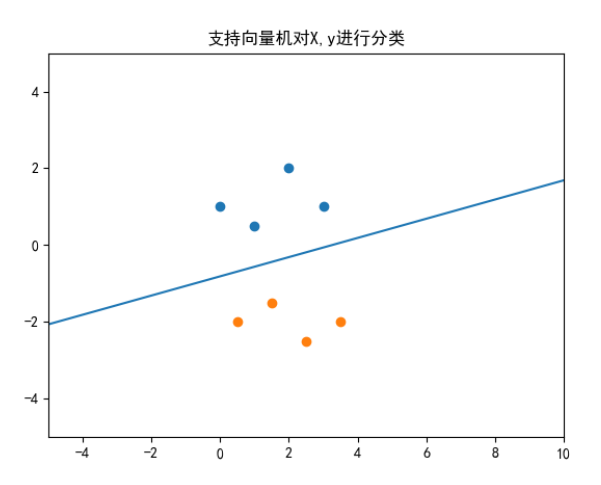
plt.title("支持向量机对X,y进行分类")
plt.show()

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from svm_smo import SVM
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
iris = datasets.load_iris()
X = np.array([[0, 1], [1, 0.5], [2, 2], [3, 1], [0.5, -2], [1.5, -1.5], [2.5, -2.5], [3.5,-2]])
y = np.array([1, 1, 1, 1, -1, -1, -1, -1]).reshape(-1, 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
model = SVM()
model.fit(X_train, y_train, N=10)
plt.axis([-1, 9, -3, 5])
plt.scatter(X_train[:, 0][y_train[:, 0] == 1], X_train[:, 1][y_train[:, 0] == 1])
plt.scatter(X_train[:, 0][y_train[:, 0] == -1], X_train[:, 1][y_train[:, 0] == -1])
x0 = np.linspace(0, 8, 200)
line = -model.w[0] / model.w[1] * x0 - model.b / model.w[1]
plt.plot(x0, line)
plt.title("y = -model.w[0] / model.w[1] * x0 - model.b / model.w[1]")
plt.text(1, 4.5, "y = -model.w[0] / model.w[1] * x0 - model.b / model.w[1]")
plt.xlabel("X")
plt.ylabel("Y")
plt.tight_layout()
plt.show()
import numpy as np
A = 6 #学号为006
#a = A * 10
x = 10
epsilon = 1e-6
def f(x):
return A-x**3
def df(x):
return -3 * x ** 2
while np.abs(f(x)) > epsilon:
x = x - f(x)/df(x)
print(f"{A}的3次方根为{x}")
牛顿迭代好像没变,改一下a = A*1就行
66
111