一文看懂！在 EdgerOS 使用红黑树有多简单轻松！

[leecactus0]

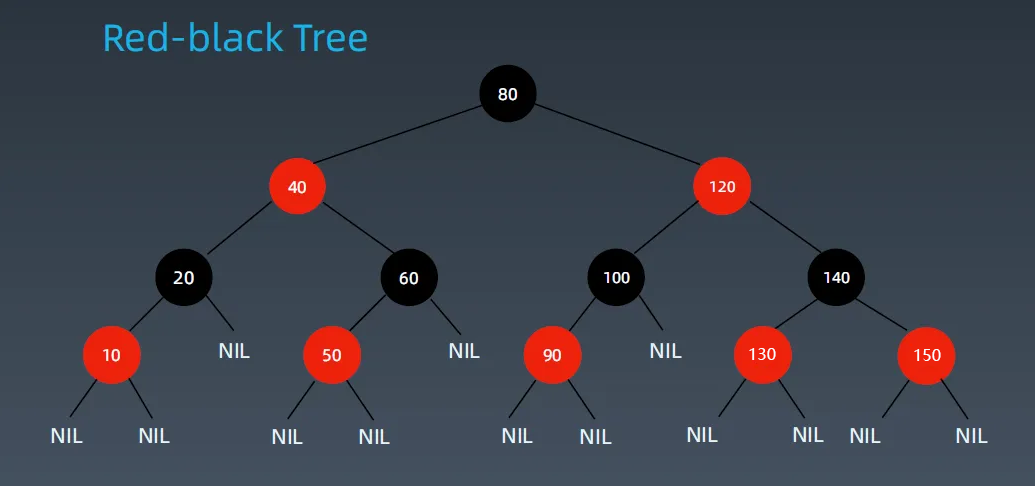
在我们学习数据结构时会经常听到一个名词—红黑树。

 

相信大家都知道红黑树是一个比较复杂的数据结构，但其中的运行原理和规则可能并不清楚，而现在日常开发中我们也很少有机会直接接触到红黑树的实例，取而代之的是使用通过红黑树构建出来的产品和工具。比如 Java 中的 TreeSet 和 TreeMap，C++ STL 中的 Set，Map,以及 Linux 虚拟内存的管理，都是用通过红黑树去实现的，除此之外 Node.js 的定时器管理中也有红黑树的存在。

 

那么红黑树到底是什么？为什么要使用红黑树？对于这些问题本文将带大家一起去寻找答案。

 

红黑树的起源

二叉树

红黑树起初是由二叉树逐渐演变过来的，要了解红黑树，首先就要搞清楚什么是二叉树。

二叉树中我们常用到的结构模型为二叉查找树，它的每个节点的值都大于其左侧树的任意节点而小于右侧子树的任意节点。

 

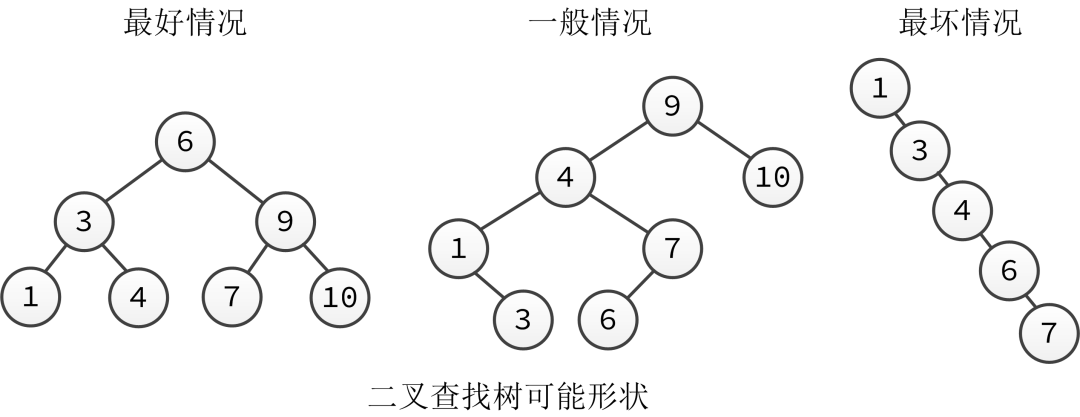
而上图的展示的则是二叉树有可能形成的形状。二叉树的形状决定了查找时所需要的运行时间，而向树中插入节点的顺序又决定了树的形状。在最坏情况下，二叉树就变成了一个链表，所以为了保证运行时间始终在对数级别（也就是树的分支相对平衡）降低树的高度，那么就需要在二叉树插入数据时动态的进行树形调整，从而保证二叉树的平衡而这样始终可以保持平衡的二叉树就被称为平衡二叉树（AVL 树）。

 

AVL 树

 

AVL 树也称为自平衡二叉树，它在二叉树的基础上新增一条规则为“每个节点的左右子树高度之差不超过 1 ”，在插入或删除节点时，树的平衡被打破就会通过树旋转来重新调整整棵树的形状直至树再次恢复平衡。这也是我们经常听到的二分查找法的原型。

 

但如果每次添加一个节点都会导致树的一次或多次的旋转这样会极大的消耗性能，树旋转的意义在于降低树的高度，降低高度可以提升查询速度。但是对于高密度的插入场景，显然自平衡二叉树花费在树旋转上的代价有些过高。

 

那么有没有更好的方案，在不借助频繁旋转的情况下也可以降低树的高度呢？当然有那就是 2-3-4 树。

 

2-3-4 树

 

AVL 通过动态的树旋转降低树的高度，那如果在二叉树上每一个节点可以保存多个值，变成多叉树，是否也能达到同样降低树高度的效果呢? 答案是一定的，这就是 2-3-4 树 的树形结构。

 

2-3-4 树在标准二叉树上每个节点可以保存多个值，保存两个值时可以对应 3 个子节点，保存 3 个值时可以对应 4 个子节点。如图所示：

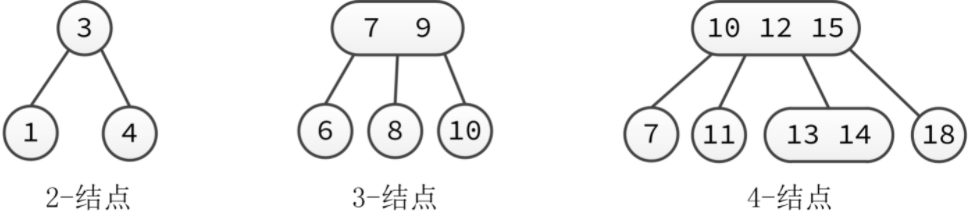
2-3-4 树是 4 阶 B 树，所有叶子节点都在相同的深度上，4 阶表示任意节点最多连接 4 个子节点，但大多数编程语言直接实现 4 阶 B 树是比较困难的，这个时候就体现出了红黑树的优势了。红黑树相当于是 4 阶 B 树的一个特殊实现。红黑树的树形依旧采用二叉树的方式，只不过为节点引入了颜色属性。

 

红黑树

红黑树依旧是 2 叉树，不过红黑树在 2 叉树的基础上又引入了一个颜色属性：

• 黑色表示普通节点

• 红色表示可与父节点合并看做多值节点

   

而红黑树也遵从这几个性质：

1.每个结点都是红色或黑色的

2.根结点是黑色的（是红色最终也会转黑色）

3.所有叶子结点都是黑色的，这里的叶子结点指的是空结点，常用 NIL 表示

4.如果结点为红色，则其子结点均为黑色（红色表示可与父结点合并）

5.从给定结点到其任何后代 NIL 结点的每条路径都包含相同数量的黑色节点（转成 2-4 树，所有叶子节点均在最底层）

 

而红黑树中的旋转和颜色翻转则对应的 4 阶 B树中的拆分和合并。

 

 

插入节点

 

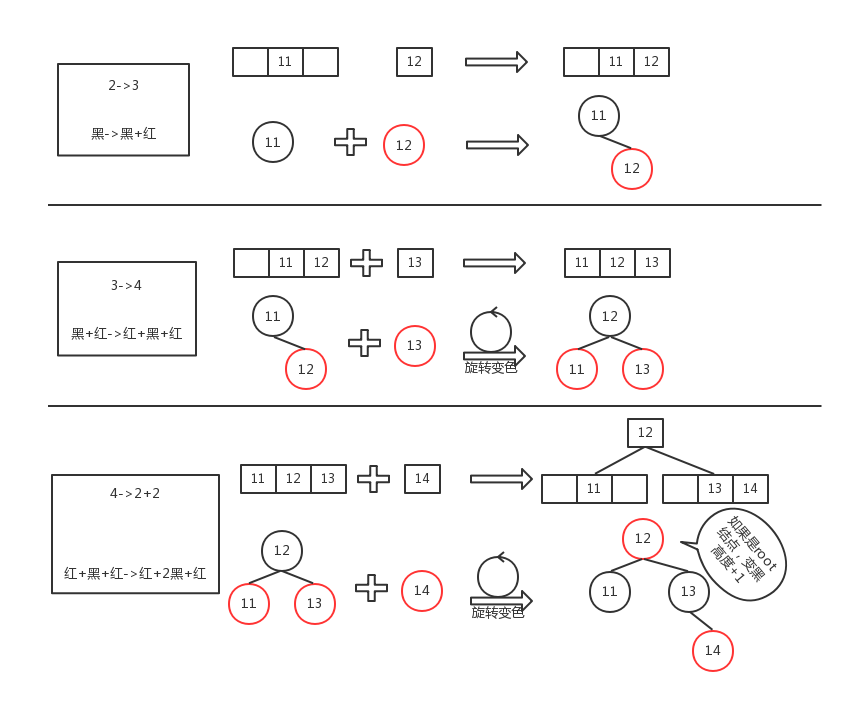
2-3-4 树中结点添加需要遵守以下规则：

• 插入都是向最下面一层插入

• 升元：将插入结点由 2-结点升级成 3-结点，或由 3-结点升级成 4-结点

• 向 4-结点插入元素后，需要将中间元素提到父结点升元，原结点变成两个 2-结点，再把元素插入 2-结点中，如果父结点也是 4-结点，则递归向上层升元，至到根结点后将树高加 1

   

而将这些规则对应到红黑树里，就是：

• 新插入的结点颜色为红色，这样才可能不会对红黑树的高度产生影响

• 2-结点对应红黑树中的单个黑色结点，插入时直接成功（对应 2-结点升元）

• 3-结点对应红黑树中的黑+红子树，插入后将其修复成 红+黑+红 子树（对应 3-结点升元）

• 4-结点对应红黑树中的红+黑+红子树，插入后将其修复成红色祖父+黑色父叔+红色孩子子树，然后再把祖父结点当成新插入的红色结点递归向上层修复，直至修复成功或遇到 root 结点

   

删除节点

 

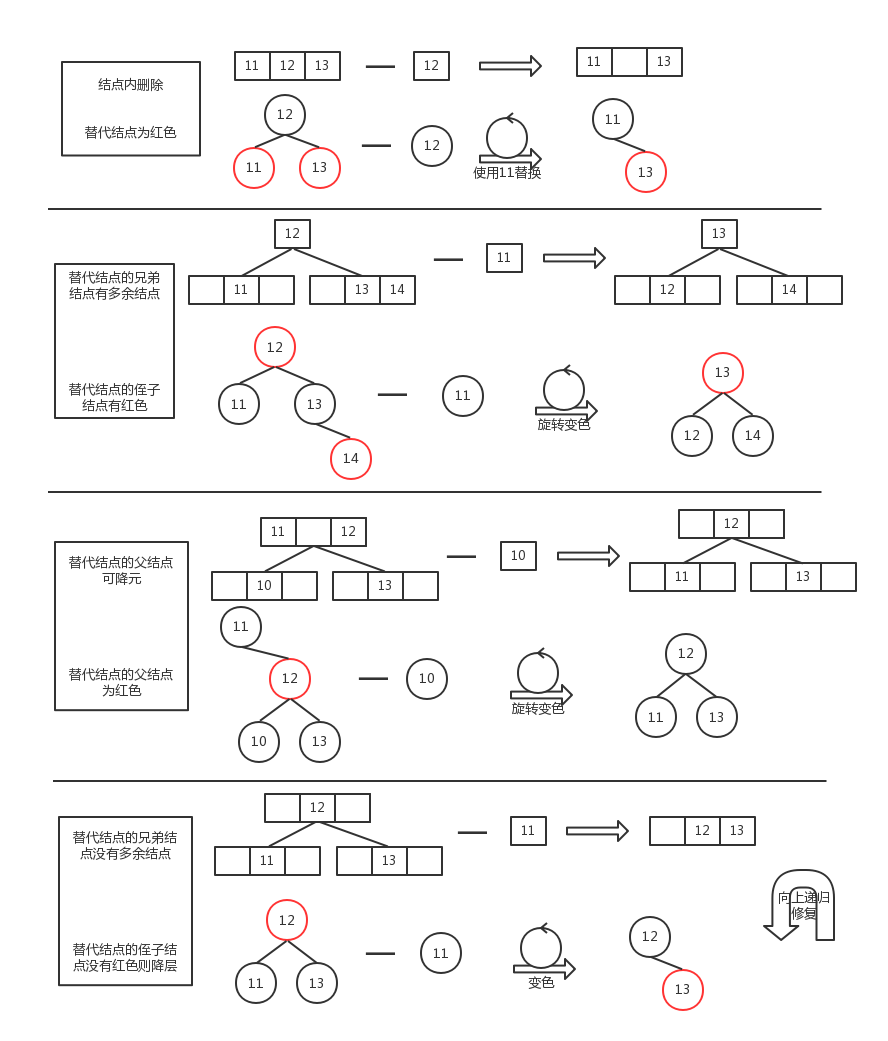
红黑树的删除要比插入要复杂一些，我们还是类比 2-3-4 树来讲：

• 查找最近的叶子结点中的元素替代被删除元素，删除替代元素后，从替代元素所处叶子结点开始处理

• 降元：4-结点变 3-结点，3-结点变 2-结点

• 2-结点中只有一个元素，所以借兄弟结点中的元素来补充删除后的造成的空结点

• 当兄弟结点中也没有多个元素可以补充时，尝试将父结点降元，失败时向上递归，至到子树降元成功或到 root 结点树高减1

   

将这些规则对应到红黑树中即：

• 查找离当前结点最近的叶子结点作为替代结点（左子树的最右结点或右子树的最左结点都能保证替换后保证二叉查找树的结点的排序性质，叶子结点的替代结点是自身）替换掉被删除结点，从替代的叶子结点向上递归修复

• 替代结点颜色为红色（对应 2-3-4 树中 4-结点或 3-结点）时删除子结点直接成功

• 替代结点为黑色（对应 2-3-4 树中 2-结点）时，意味着替代结点所在的子树会降一层，需要依次检验以下三项，以恢复子树高度：

  • 兄弟结点的子结点中有红色结点（兄弟结点对应 3-结点或 4-结点）能够“借用”，旋转过来后修正颜色

• 父结点是红色结点（父结点对应 3-结点或 4-结点，可以降元）时，将父结点变黑色，自身和兄弟结点变红色后删除

• 父结点和兄弟结点都是黑色时，将子树降一层后把父结点当作替代结点递归向上处理

 

是不是通过上面的内容已经对红黑树的前世今生有了充分的认识了，但实际上了解归了解，如果要让我们自己来完成一套关于红黑树的控制模块，还是有些工作量的。但大家也应该了解到了红黑树的使用非常重要，在软件的世界里无处不在，重要性可想而知。

 

为了减少开发者的对于红黑树的开发量，EdgerOS 系统中也集成了关于红黑树的控制模块。我们不再需要手动实现红黑树原理，只需要简单的调用接口便可以完成对红黑树实例的增删改查。

 

EdgerOS 红黑树模块

EdgerOS 封装的红黑树模块，仅仅需要提供一个比较器函数，使用起来远比理解红黑树更加简单。

var tree = new RBTree(function(k1, k2){
  if (k1 < k2)
    return-1;
  else if (k1 > k2)
    return1;
  else
    return 0;
});

完整的红黑树使用 

var RBTree =require('rbtree');
var tree = new RBTree(function(k1, k2){
  if (k1 < k2)
    return -1;
  else if (k1 > k2)
    return 1;
  else
    return 0;
});  
 
// 向红黑树插入数据
tree.put(1, 'Hello'); 
tree.put(3, 'EdgerOS');
tree.put(2, 'World');
 
 // 遍历红黑树
tree.inorder(function(key, value){
  // 顺序输出 1, 2, 3
  console.log('ID:', key,'NAME:', value);
});

在 EdgerOS 上使用红黑树是不是格外的简单？希望这篇文章能对你有所帮助。除此之外 EdgerOS 也为开发者提供丰富的基础模块降低开发难度，助力开发者们可以在 EdgerOS 上更加轻松的开发出更多优秀的应用。

 

更加详细的红黑树接口可以在 EdgerOS 官方文档中获取。

EdgerOS 红黑树文档：https://www.edgeros.com/edgeros/api/BASIC%20COMPONENTS/General/rbtree.html