数组——3. 二维数组

[天將明°]

二维数组

二维数组定义的一般形式如下：

类型说明符 数组名[常量表达式1][常量表达式2]

与一维数组的定义唯一的不同是多了一个常量表达式2，其中，常量表达式1为第一维的长度，常量表达式2为第二维的长度。通常在处理二维数组的时候，为了便于理解，都将数组视为一个矩阵，常量表达式1表示矩阵的行数，而常量表达式2表示矩阵的列数。与一维数组一样，在定义二维数组时，常量表达式同样不能为变量。下面先通过一段代码来看二维数组的定义。

#include<stdio.h>

#define M 4
#define N 3


int main()
{
    int arr[M][N];
    for (int i = 0; i < M; i++)
    {
        for (int j = 0; j < N; j++)
        {
            printf("&arr[%d][%d]=%p\t", i, j, &arr[i][j]);
        }
        printf("\n");
    }
    return 0;
}

运行结果：

&arr[0][0]=00AFFC18     &arr[0][1]=00AFFC1C     &arr[0][2]=00AFFC20
&arr[1][0]=00AFFC24     &arr[1][1]=00AFFC28     &arr[1][2]=00AFFC2C
&arr[2][0]=00AFFC30     &arr[2][1]=00AFFC34     &arr[2][2]=00AFFC38
&arr[3][0]=00AFFC3C     &arr[3][1]=00AFFC40     &arr[3][2]=00AFFC44

将二维数组arr视为一个矩阵，下图显示了数组中每个元素在矩阵中的存放位置。

数组中各个元素在矩阵中对应的位置由二维数组的两个下标决定。我们可以将定义的二维数组int arr[4] [3]视为由arr[4] 和int [3] 两部分构成，将arr[4]视为一个整型一维数组，其中含有4个元素arr[0]、arr[1]、arr[2]、arr[3]，每个元素都是int[3]类型的，也就是说，每个元素又是一个一维数组，每个一维数组含有3个元素，如arr[0]含有arr[0] [0]、arr[0] [1]、arr[0] [2]三个元素。

二维数组中的所有元素都存储在一片连续的内存单元中，所占用的内存大小为元素类型所占用的内存大小乘以第一维及第二维的长度。如果以矩阵的方式来分析二维数组的存储方式，那么先从矩阵第一行从左往右依次存储完所有元素，然后按照同样的方法存储第二行的所有元素，直到存储完所有数组元素为止。

接下来再看一个二维数组的示例：

任意输入一个3行3列的二维数组，求对角元素之和

int main()
{
    int arr[3][3];
    int i, j, sum = 0;
    printf("please input:\n");
    for (i = 0; i < 3; i++)
    {
        for (j = 0; j < 3; j++)
        {
            scanf("%d", &arr[i][j]);
        }
    }
    for (i = 0; i < 3; i++)
    {
        for (j = 0; j < 3; j++)
        {
            if (i == j)
            {
                sum += arr[i][j];
            }
        }
    }
    printf("the result is: %d\n", sum);
    return 0;
}

运行结果：

please input:
1 2 3
4 5 6
7 8 9
the result is: 15

例题

矩阵转置

矩阵转置图示：

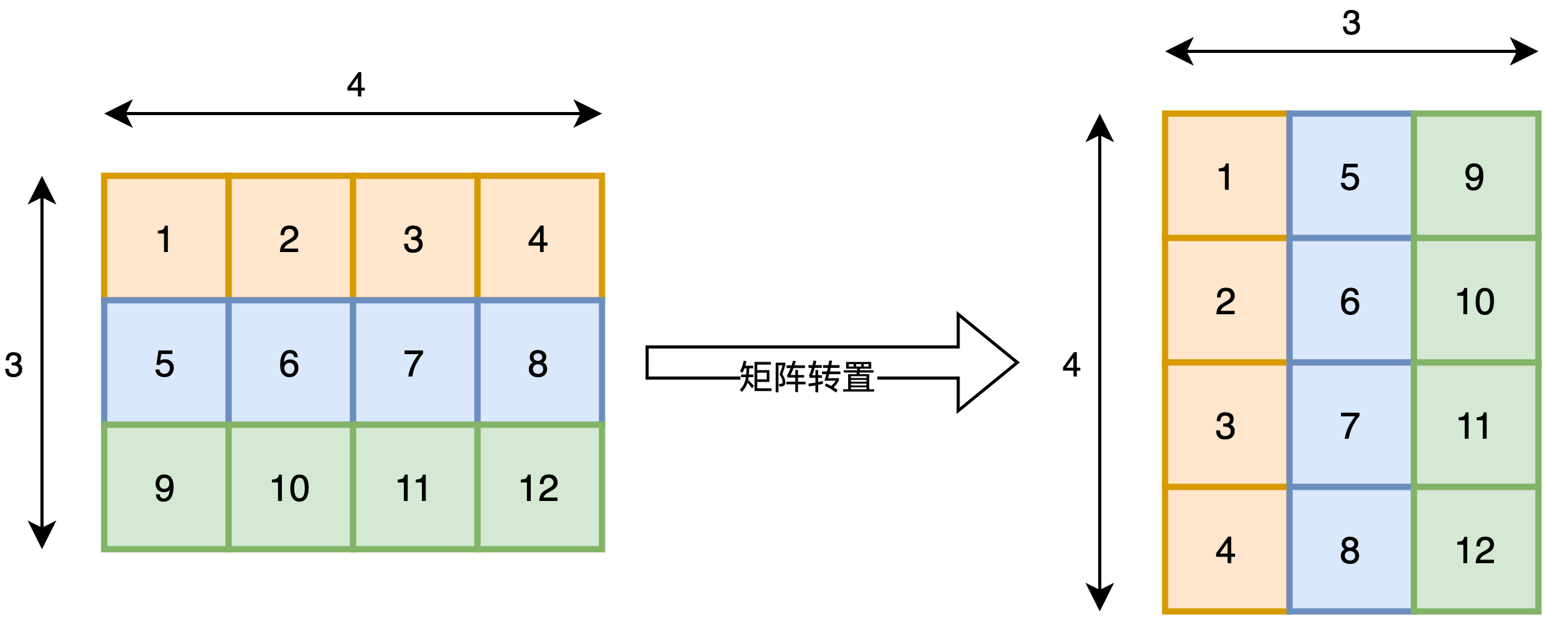
基于二维数组实现矩阵转置，以下选项对应(1)处缺失的代码，请判断哪一项无法实现矩阵转置。

#include <stdio.h>
#define LEN 101

void print_matrix(int mat[][LEN], int row, int col)
{
    for (int i = 0; i < row; ++i)
    {
        for (int j = 0; j < col; ++j)
            printf("%d\t", mat[i][j]);
        printf("\n");
    }
}

int main(int argc, char** argv)
{
    int i, j, row, col, num, m[LEN][LEN], t[LEN][LEN];

    printf("请输入矩阵的行数(<=100)：");
    scanf("%d", &row);
    printf("请输入矩阵的列数(<=100)：");
    scanf("%d", &col);
    num = row * col;
    printf("请输入矩阵的元素(共%d个，空格分隔)：\n", num);
    for (i = 0; i < row; ++i)
        for (j = 0; j < col; ++j)
            scanf("%d", &m[i][j]);

    printf("转置前：\n");
    print_matrix(m, row, col);

    (_____1_____)

    printf("转置后：\n");
    print_matrix(t, col, row);

    return 0;
}

A：正确

    for (i = row - 1; i >= 0; --i)
        for (j = col - 1; j >= 0; --j)
            t[j][i] = m[i][j];

B：错误

越界，且第一行没转换

    for (i = 1; i <= row; ++i)
        for (j = 1; j <= col; ++j)
            *(*(t + j) + i) = *(*(m + i) + j);

C：正确

    for (i = 0; i < row * col; ++i)
        t[i / row][i % row] = m[i % row][i / row];

D：正确

    for (i = 0; i < row; ++i)
        for (j = 0; j < col; ++j)
            t[j][i] = m[i][j];