64,191
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享目录
do i++; while(q[i] < x); //用while(q[++i]= x)也是等价的语句>
do j--; while(q[j] > x); 会使得 q[j+1..r] >= x, q[j] <= x
if(i < j) swap(q[i], q[j]); 会使得 q[l..i] <= x, q[j..r] >= x
六.顺便给出从大到小快排的模板(只需要改动两个大小符号即可)
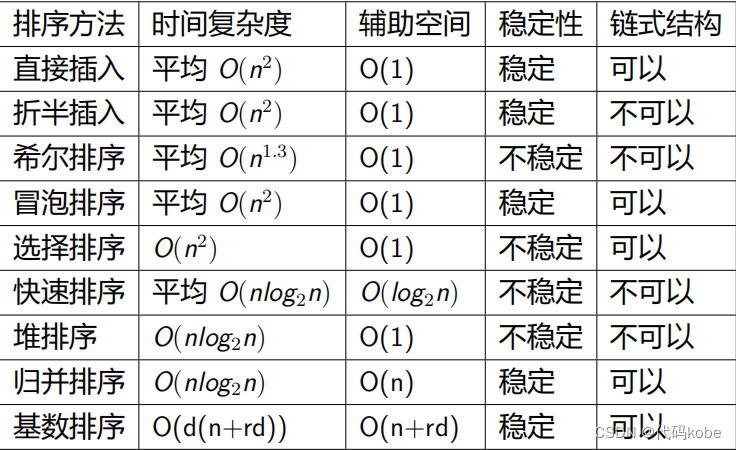
排序问题可以说是最经典的算法问题了,一般一开始学的基础算法就是排序,排序既是算法的基础,也是考研数据结构的重要知识点。但是 C/C++ 都有现成的库函数(C里是 qsort、C++是sort),所以导致很多人就没有学排序算法本身,其实排序算法的思路非常有意思,从最简单的学起,对以后学习复杂算法是非常有帮助的,比如快速排序和快速选择之间的关系,归并排序和逆序对之间的关系。
从今天开始,我们来试着掌握每个排序算法的思路,今天是快速排序。
快速排序,采用的是分治的思想,选择一个基准点,把所有小于基准点的数放到它左边,把所有大于基准点的数放到它右边,如图所示:
| 图示 | 含义 |
| ■ 蓝色的柱形 | 表示还未排序的数 |
| ■ 黄色的柱形 | 表示随机选定的基准数 |
| ■ 橙色的柱形 | 表示已经排好序的数 |
| ■ 红色的柱形 | 表示正在遍历比较的数 |
| ■ 绿色的柱形 | 表示比基准数小的数 |
| ■ 紫色的柱形 | 表示比基准数大的数 |
原始数据:
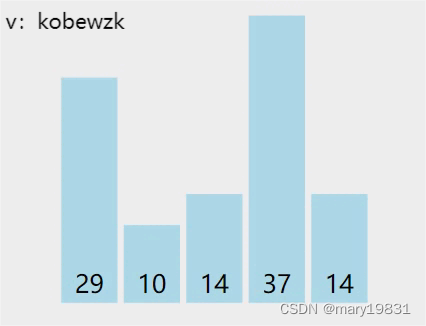
排序可视化过程:
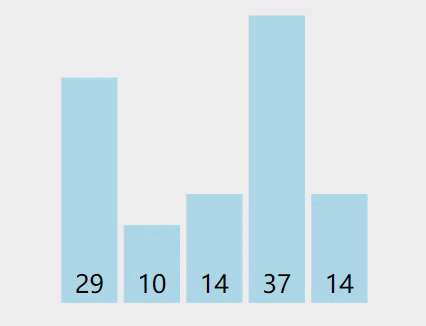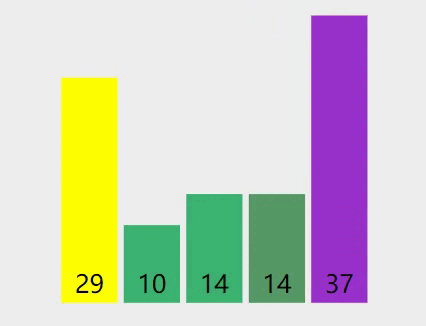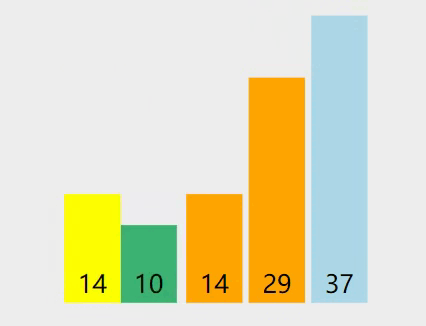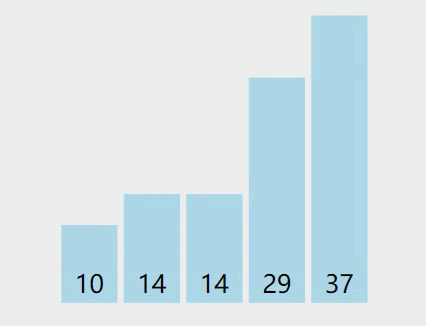
容易发现:第一次遍历选择的基准数是29,第一遍排序结束的结果是14,10,14,29,37,也就是29左边的数都小于等于29,29右边的数都大于等于29,符合我们对快速排序算法的定义,在此基础上递归排序即可
给你一个长度为n(n<=100000)的整数数组a,请你将该数组升序排列
先给出我个人的万能模板(个人习惯以j分界,文章后面详细说明怎么用i分界):
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int q[N];
void quicksort (int q[],int l, int r)
{
if (l>=r) return ;
int i=l-1,j=r+1,x=q[(l+r)/2];
while(i<j)
{
do i++;while(q[i]<x);
do j--; while(q[j]>x);
if(i<j) swap(q[i],q[j]);
}
quicksort(q,l,j);
quicksort(q,j+1,r);
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&q[i]);
}
quicksort(q,0,n-1);
for(int i=0;i<n;i++)
{
printf("%d ",q[i]);
}
}
算法证明: 借鉴算法导论的循环不变式的方法
快排核心模板:
1.递归出局
2.处理某个子问题
3.递归处理子问题
//循环体
void quicksort(int q[], int l, int r)
{
//第一步:规定递归的终止情况
if(l >= r) return;
//第二步:分成子问题,注意i和l的初始位置,待会详细说明为什么这么设置i和j和x
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while(i < j)
{
do i++; while(q[i] < x);//注意不能有等于,待会详细说明为什么不能有等于
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
//第三步:以j为分界,划分区间,递归处理子问题
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
证明目标:循环不变式,即任意一次while循环(除了最后一次while循环)结束后,q[l..i] <= x,q[j..r] >= x
证明过程:
1.初始化:i = l - 1, j = r + 1,显然此时q[l..i],q[j..r]为空,证明目标显然成立
2.保持:假设下一轮循环开始之前的循环不变式成立,即 q[l..i] <= x , q[j..r] >= x
执行上述的循环体
do i++; while(q[i] < x); //用while(q[++i]<x)也是等价的语句
会使得 q[l..i-1] <= x, q[i] >= xdo j--; while(q[j] > x);
会使得 q[j+1..r] >= x, q[j] <= xif(i < j) swap(q[i], q[j]);
会使得 q[l..i] <= x, q[j..r] >= x所以,经过循环体之后,循环不变式依然成立
注:由于i和j的设定问题,i和j必须要先自增!!否则在特殊情况(比如去q[i]和q[j]都等于x)下就会死循环
比如:
while(q[i] < x) i++;
while(q[j] > x) j--;
当q[i]和q[j]都为 x 时, i 和 j 都不会更新,导致 while 陷入死循环
3.终止:最后一轮循环结束时 j <=i且只有j+1=r或者j=r两种情况
1.以j划分时,随机值x为什么不能选q[r],以i划分时,随机值x为什么不能选q[l]
证明:假设x取q[r],关键问题在于递归子问题 quick_sort(q, l, j), quick_sort(q, j + 1, r);举例来说,若x选为q[r],且数组中q[l..r-1] < x,那么一轮循环结束时,i = r, j = r,quick_sort(q, l, j)直接退出函数调用,没有排序,以i划分也是同理
2. do i++; while(q[i] < x)和do j--; while(q[j] > x)为什么不能用q[i] <= x 和 q[j] >= x
证明:假设q[l..r]全相等,则执行完do i++; while(q[i] <= x);之后,i会自增到r+1,然后继续执行q[i] <= x 判断条件,造成数组下标越界
3. if(i < j) swap(q[i], q[j])能否使用 i <= j
证明:可以。因为 i = j 时,交换一下q[i],q[j] 无影响,因为马上就会跳出循环了
4.最后一句能否改用左区间quick_sort(q, l, j-1),右区间 quick_sort(q, j, r)作为划分(用i做划分时也有同样的问题)
证明:不能。
情况一:i=j+1时,显然根据上述循环体的结论同意得到q[l,..j]<=x,q[i,..r](即q[j+1,r])>=x,因此我的原代码的划分一定正确。但是倘若使用上述错误的划分,q[l,..j-1]<=x,没有问题,但是q[j]<=x,却被递归在右半个区间,显然错误
情况二:i=j时,特殊情况i=j=1时,此时很容易得到q[i]=q[j]=x,倘若用上述的错误代码,左边区间调用函数会直接退出,但是右边区间等价于原来的情况原地踏步,所以该划分方式会导致死循环
void quick_sort(int q[], int l, int r)
{
if(l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r + 1 >> 1];//注意是向上取整,因为向下取整可能使得x取到q[l],这是和j划分不一样的地方
while(i < j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
quick_sort(q, l, i - 1), quick_sort(q, i, r);//不用q[l..i],q[i+1..r]划分的道理和分析4中j的情况一样
}
void quicksort(int q[], int l, int r)
{
if(l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while(i < j)
{
do i++; while(q[i] > x); // 这里和下面
do j--; while(q[j] < x); // 这行的判断条件改一下
if(i < j) swap(q[i], q[j]);
}
quicksort(q, l, j), quicksort(q, j + 1, r);
}
如果觉得有问题欢迎私聊,如果绝对写的不错,欢迎支持,创作不易。