145
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享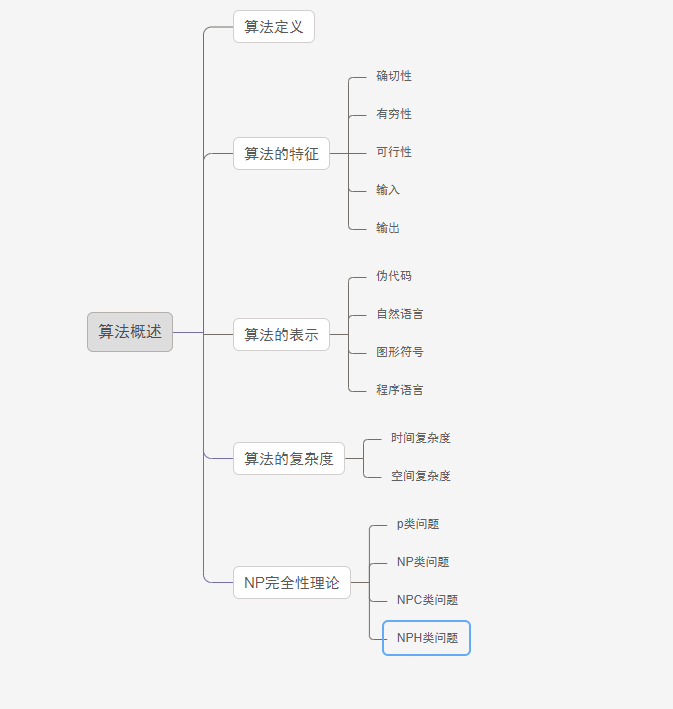
目录
是一系列解决问题的明确指令,即对符合一定的规范的输入,能够在有限的时间内获得输出,每条指令表示一个或多个操作。
O(1):称为常数级,运行时间与问题规模n没有关系
O(logn):称为对数级;
O(n):称为线性级,遍历、扫描全部输入
O(nlogn):许多分治算法和在树上工作的算法;
O(n^c):称为多项式级;
O(c^n):称为指数级;
O(n!):称为阶乘级,最低效的算法,常见于某些排列组合问题中的暴力求解。;
常见复杂度排序:O(1)< O(log2 n) < O(n) < O(nlog2 n) < O(n^2) < O(n^3) < O(2^n) <O(n!) < O(n^n)
算法的复杂度有:最好情况、最差情况还有平均情况,一般来说最好情况指在理想情况下运行的时间,最坏情况是指在需要的时间的最小值,平均情况是一般情况下需要的时间。
按照符号O的定义,容易证明它有如下运算规则:
a、O(f)+O(g)=O(max(f,g))
b、O(f)+O(g)=O(f+g)
c、O(f)O(g)=O(fg)
d、如果g(N)=O(f(N)),则O(f)+O(g)=O(f)
e、O(Cf(N))=O( f(N)),其中C是一个正的常数
f、f=O(f)bc
①P问题必定是NP问题,但现目前还无法证明NP问题是否是P问题
②NPC问题必定是NP问题,是最难的NP问题
③NPC问题也必定是NPH问题
④NPH问题不一定是NP问题
通过第一章的学习,学习到了最基本的算法知识,加深了对算法的理解,对于算法的定义,特征以及对算法的时间空间复杂度有了深一层理解,对于一些基本的算法的时间复杂度也有了一定的了解,如:冒泡排序的平均复杂度为O(n²),堆排序快速排序的时间复杂度为O(nlogn),基数排序的时间复杂度为O(N*M)等。同时明白了在很多问题中,时间和空间是一个对立面:为算法分配更多的空间,可以使算法运行的更快,反之,当空间是一个重要因素时,则需要用算法运行时间去换取空间,所以时间和空间在很多时候不能兼得。同时刚开始对于p类,NP类问题不太理解,通过后续的学习逐渐明白了道理,也对其概念有了自己的理解。
1.N鸡问题:用N元钱买N只鸡,公鸡每只5元,母鸡每只3元,小鸡1元3只,N元钱必须刚好买N只鸡,鸡必须整只买,有几种买法呢?
a = open('input.txt', 'r')
input = int(a.read())
f = open('output.txt', 'w')
print('总共有{}元\n'.format(input), file=f)
count = 0;
#公鸡:x 母鸡:y 小鸡:z
for x in range(int(input/5)+1):
for y in range(int(input/5)+1):
z = input - x - y
if (5 * x + 3 * y + z / 3) == input:
f.write('公鸡:%d 母鸡:%d 小鸡:%d\n' % (x, y, z))
count += 1
print('共有{}种方法 \n'.format(count), file=f)
a.close()
f.close()
输入:200
输出:
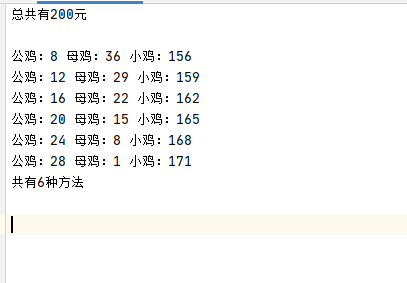
时间复杂度:时间复杂度为O(n^2)。
2.统计数字问题:一本书的页码从自然数1 开始顺序编码直到自然数n。书的页码按照通常的习惯编排,每个页码都不含多余的前导数字0。数字计数问题要求对给定书的总页码(n<=200000),计算出书的全部页码中分别用到多少次数字0,1,2,…,9。
f = open('input.txt', 'r')
n = int(f.read())
f.close()
l = [0] * 10
for i in range(1, n + 1):
while i:
a = (i % 10)
l[a] += 1
i = int(i / 10)
f = open('output.txt', 'w')
f.write("页码总数是{}\n \n0出现{}次,\n1出现{}次,\n2出现{}次,\n3出现{}次,\n4出现{}次,\n5出现{}次,\n6出现{}次,\n7出现{}次,\n8出现{}次,\n9出现{}次".format( n, l[0], l[1], l[2], l[3], l[4], l[5], l[6], l[7], l[8], l[9]))
print("写入完毕")
f.close()
输入:200
输出:

输入:1000
输出:
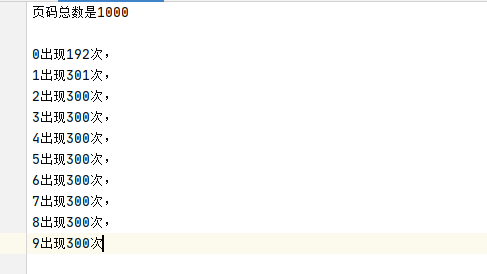
时间复杂度:时间复杂度为O(n)。