计硕三班-李纯-2022222288 第一章

纯天才 2022-10-26 23:19:02

一、学习内容

1.1 算法与程序

（1）算法是由若干条指令组成的有穷序列，其性质如下：

① 输入：有零个或多个由外部提供的量作为算法的输入。

② 输出：算法产生至少一个量作为输出。

③ 确定性：组成算法的每条指令是清晰的，无歧义的。

④ 有穷性：算法中的每条指令的执行次数是有限的，算法必须能在执行有限个步骤之后终止；执行每条指令的时间也是有限的。

⑤ 可行性：每个计算步骤都可以在有限时间内完成。

程序 = 数据结构 + 算法

（2）算法的描述方法：自然语言、图形符号（流程图）、程序语言、伪代码。

1.2 算法的复杂性分析

（1）算法的复杂性是算法运行所需要的计算机资源的量，需要时间资源的量成为时间复杂性，需要空间资源的量成为空间复杂性。

这个量应该是只依赖于要解的问题的规模、算法的输入和算法本身的函数。

（2）算法时间复杂性表示方法：假设每条语句的执行时间均为单位时间，影响运行时间的是主要基本操作语句，即占有最多比例的语句。

算法时间复杂度是用问题规模n的渐近阶函数表示法。

算法运行的有多快 = 全部语句的执行时间之和 = 全部语句的执行次数之和

≈ 主要基本操作的执行次数（问题规模n的运行时间函数）≈ 渐近阶（时间函数最高次数项）

（3）算法空间复杂性：空间复杂性对算法所消耗额外存储空间单元进行计数，即执行算法所需要的工作空间，是问题规模的函数。

在很多问题中，时间和空间是一个对立面：为算法分配更多的空间，可以使算法运行的更快；反之，空间是重要因素时，则需要算法以时间换取空间。

1.3 NP完全性理论

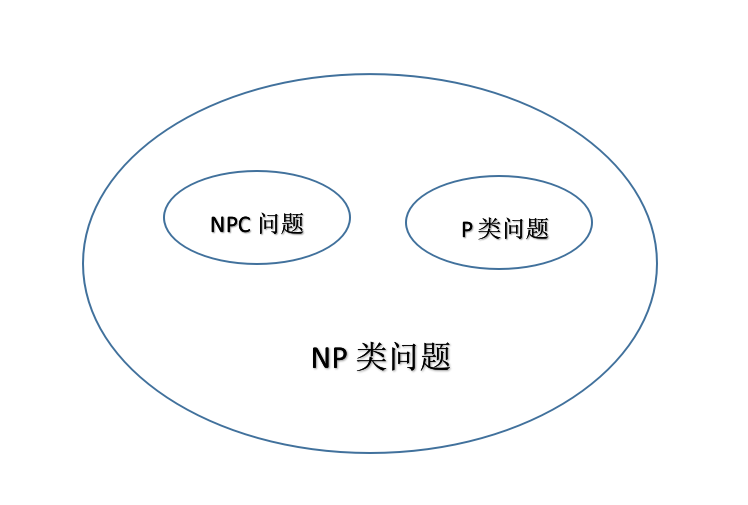
（1）P类问题（Polynomial Problem，多项式问题）：所有可以在多项式时间内求解的判定问题，P类问题是确定性计算模型下的易解问题类。

（2）NP类问题（Non-deterministic Polynomial Problem，非确定性多项式问题）：所有非确定性多项式时间内可解的判定问题，NP类问题是非确定性计算模型下的

易验证问题类。

（3）NP完全问题（NP Complete Problem）：简称NPC，令一个问题是判定问题，若该问题属于NP类问题，但是不知道该问题是否存在多项式时间的确定算法，同

时也不能证明这类问题的任何一个不存在多项式的确定算法，则称该判定问题是一个NP完全问题。

P类问题、NP类问题、NP完全问题之间的关系如下：

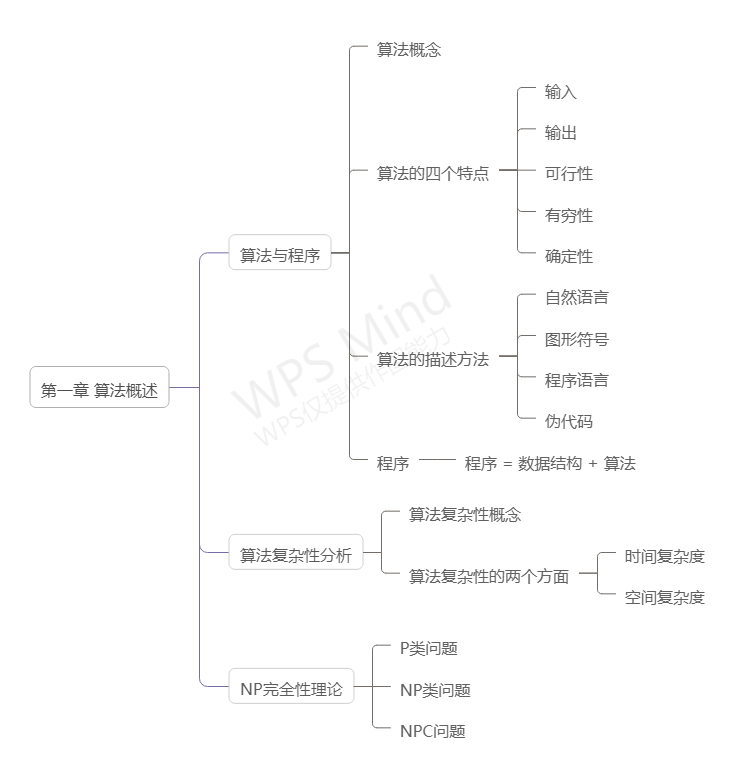
第一章思维导图如下：

二、学习心得

1. 在以前学习算法与分析课程的基础上，复习了算法的基本概念和算法复杂性的分析方法，并且根据课堂上老师举的例子能够更好的计算时间复杂度。

2. 根据书本上算法分析题的课堂讲解，了解到对于不同的时间复杂度和空间复杂度的要求下，设计的算法也会有很大的不同。通常情况下，时间与空间是不可兼得的，并且算法在最坏情况、最好情况和平均情况下的算法复杂性计算也是有所不同的，我们需要分情况进行讨论。

三、代码实现

1. N鸡问题

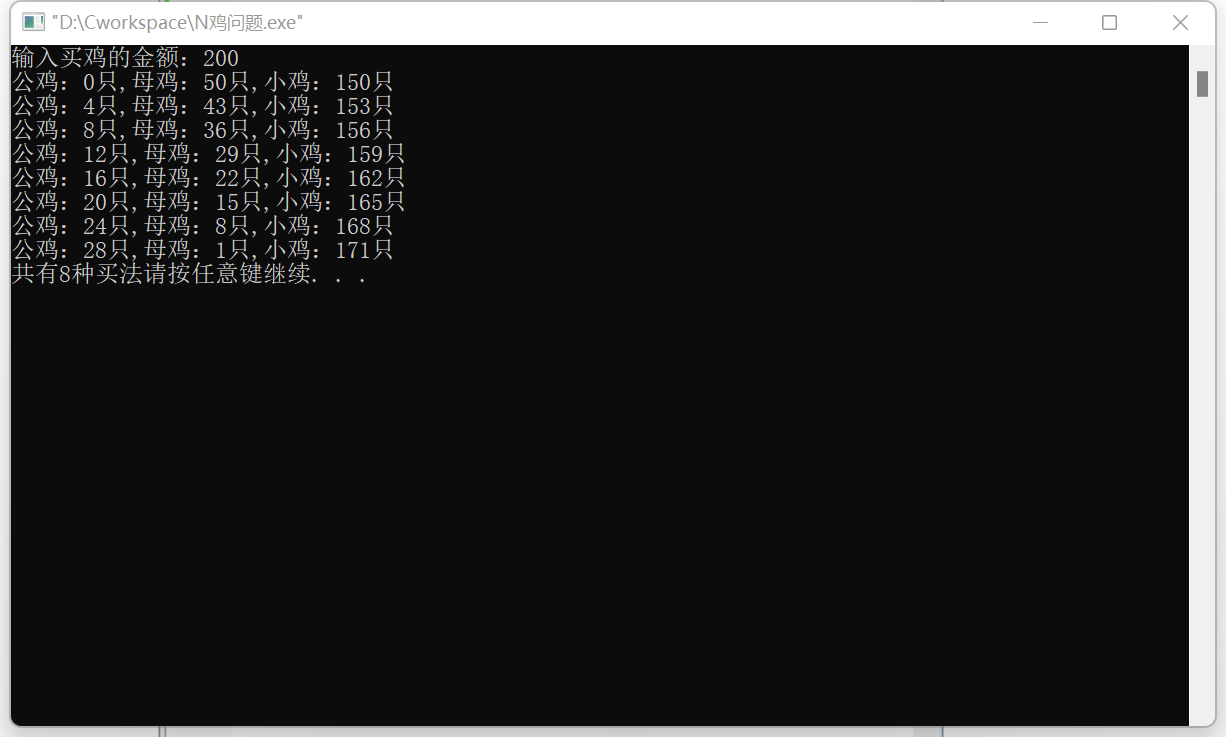
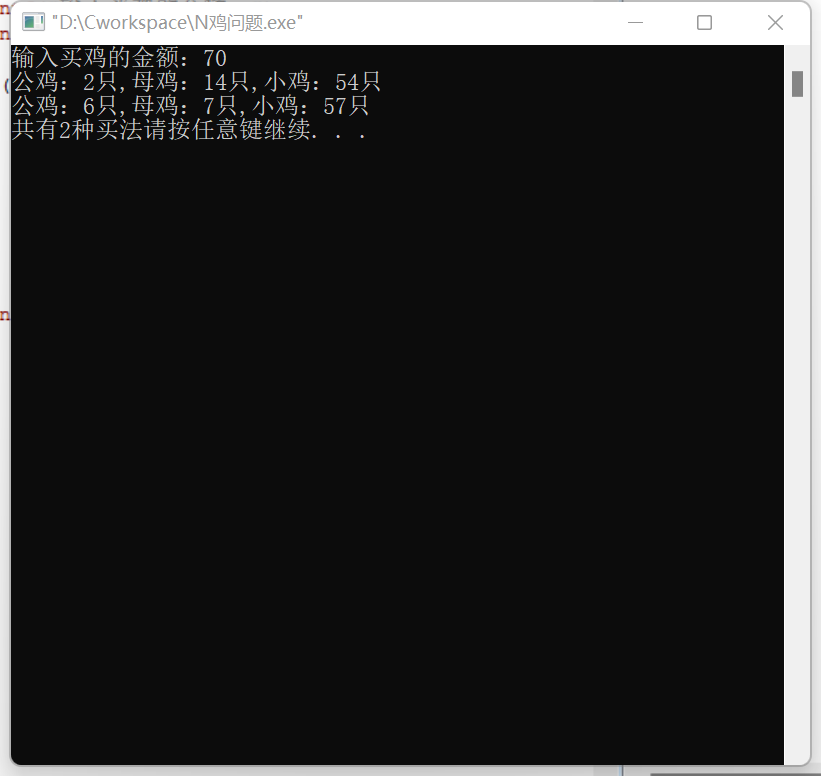
用N元钱买N只鸡，公鸡每只5元，母鸡每只3元，小鸡1元3只，N元钱必须刚好买N只鸡，鸡必须整只买，有几种买法呢？

#include<stdio.h>

int main(){
	int a,b,c; //a为公鸡 b为母鸡 c为小鸡 
	int price; //总金额 
	int k = 0; //k为几种买法 
	
	printf("输入买鸡的金额：");
	scanf("%d",&price); 
	
	for(a=0;a <= price/5;a++){
		b = (price- 7*a)/4;
		c = price - a - b;
		
		if((c%3==0)&&(5*a + 3*b + c/3==price)&&(b>0)){
			printf("公鸡：%d只,母鸡：%d只,小鸡：%d只\n",a,b,c);
			k++; 
		}
	}
	printf("共有%d种买法",k);
}

运行结果如下：

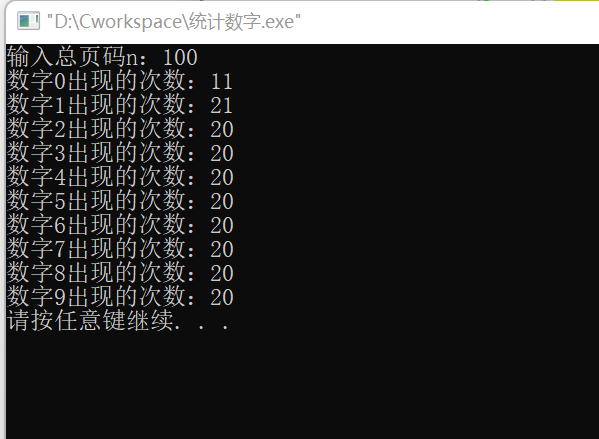
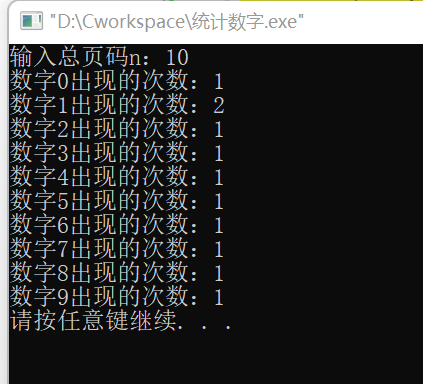
2. 统计数字问题

一本书的页码从自然数1 开始顺序编码直到自然数n。书的页码按照通常的习惯编排，每个页码都不含多余的前导数字0。

数字计数问题要求对给定书的总页码n(<=200000)，计算出书的全部页码中分别用到多少次数字0，1，2，…，9。

#include<stdio.h>

int  main(){
	int ndigit[10]; //统计数字出现次数的数组
	int n;//总页码
	int x;//当前页码
    int j;
	
	printf("输入总页码n：");
	scanf("%d",&n);
	
	//初始化数组
	for(j=0;j<10;j++){
		ndigit[j] = 0;
	} 
	
	//由高位向低位进行统计
	for(j=1;j<=n;j++){
		x = j;
		while(x){//数位分离 
			ndigit[x%10]++;//余数对应的下标数+1
			x = x/10; 
		} 
	} 
	
	for(j=0;j<10;j++){
		printf("数字%d",j);
		printf("出现的次数：%d\n",ndigit[j]);	
	}
	return 0;
}

运行结果如下：