144
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享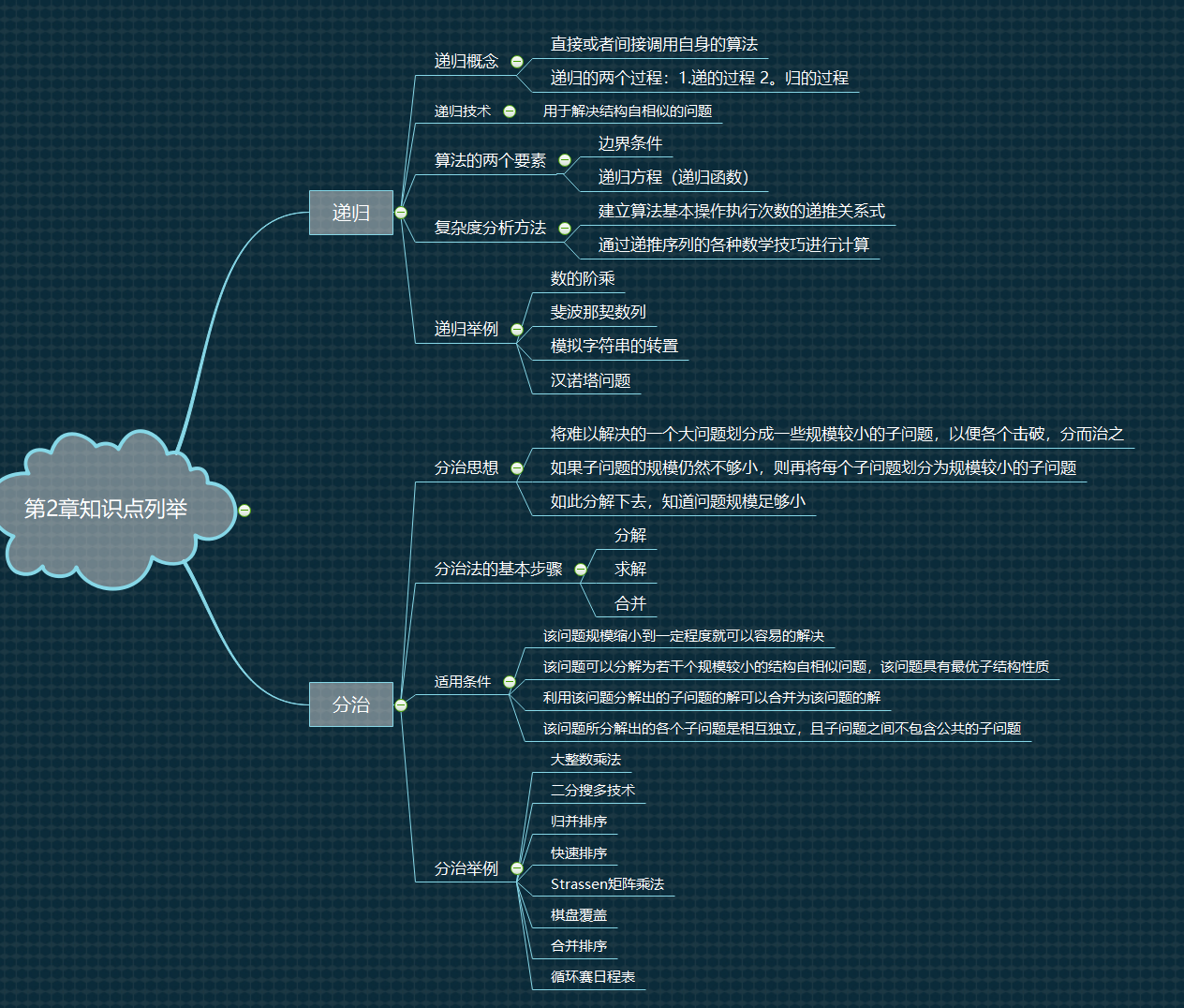
通过学习第二章节的知识,对于递归和分治有了进一步的了解。
首先,在递归技术的学习过程中,掌握了递归技术的概念,它其实就是用于去解决结构自相似的问题;可以直接或者间接的调用自身的算法,递归的两个过程;对于某一个问题使用递归求解时通常需要考虑两个要素:分别是边界条件以及递归方程(递归函数);任何算法的有效执行都需要去分析算法的时间复杂度,而递归算法的时间复杂度我们主要是利用其建立算法基本操作执行次数的递推关系式,然后利用递推关系式的各种数学技巧来进行计算;对于常见的几种递归算法使用了python语言进行代码实现。
其次,在分治技术的学习中,掌握了它的基本设计思想,对于某个特定问题我们先判定该问题是否可以使用分治技术进行求解,如果该问题满足分治法的使用条件,我们可以通过分解,求解以及合并三步骤进行问题的求解。
最后,虽然掌握了以上知识,但对于以下几个问题的理解还存在诸多不足:1.在分治算法有关于大整数乘法的时间复杂度分析只理解部分,需要进一步去进行学习和推导相关复杂度分析的递推关系式。2.实现Strassen矩阵乘法的算法代码出现了问题,通过查找相关博客后得到了解决,但在解决此问题的过程中,也发现自己的编程能力非常一般,往后的学习过程中还需要多练习算法,包括对于算法的设计,优化以及时间复杂度的分析。
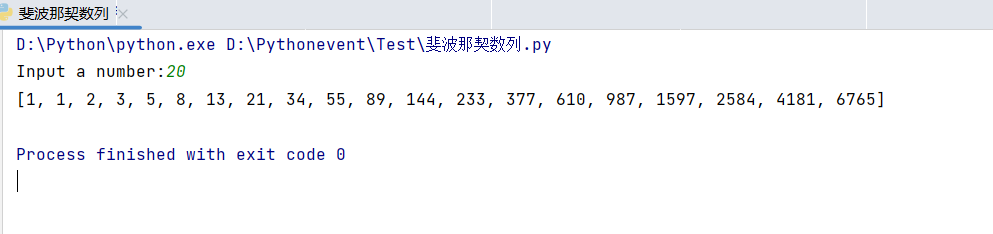
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用,为此,美国数学会从 1963 年起出版了以《斐波那契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
#用递归的方法,加上while循环,把每次循环产生的新项增加到数列最后,最后一次性输出list
def fibonacci4(n):
list = []
i = 0
while i < n:
if i == 0 or i == 1:
list.append(1)
else:
list.append(list[i-2] + list[i-1])
i = i + 1
print(list)
if __name__ == '__main__':
n = int(input('Input a number:'))
fibonacci4(n)

使用递归树的方式来计算斐波那契数列的时间复杂度
这里假设我们在递归的最后两层进行了n次操作
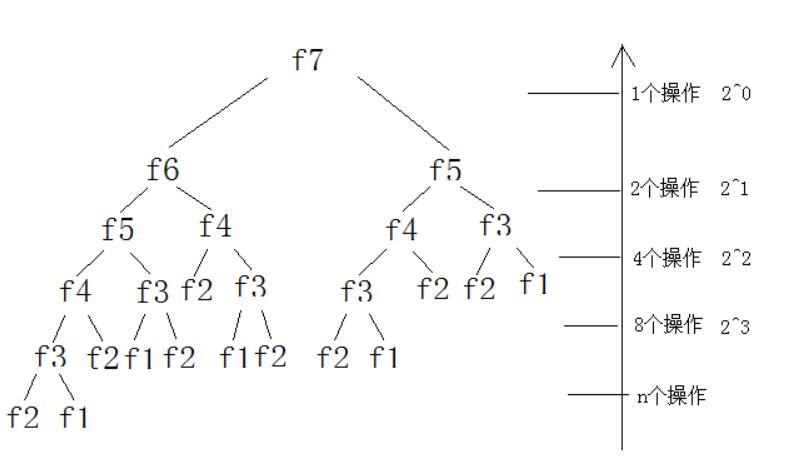
由斐波那契的递归树图我们可以看出,从下到上进行递归运算的时候,程序运行的次数是以2^x方式增加的。
我们来计算一下f(7)的运行次数
想要得到运行次数,首先我们要得到递归的深度,其中有2层为基本层
n = 7 - 2 = 5
计算运行次数
T(n) = 2^0 + 2^1 + 2^2 + 2^3 + n = 2^4 + n -1
如果递归的深度足够深的话,最后两个基数层的(n-1)次相比于2的指数级可以忽略不计,所以斐波那契的时间复杂度为
O(fib(n)) = O(2^n)
很容易想到采用递归的思想,即N个数,只要前面N-1个数字已经生成的全排列,只用将N插入到这些排列中,生成新的排列顺序。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def sort_print(List, start, end):
if start >= end - 1:
print(List)
else:
i = start
for index in range(start, end):
List[index], List[i] = List[i], List[index]
sort_print(List, start + 1, end)
List[index], List[i] = List[i], List[index]
if __name__ == '__main__':
m = int(input('Input a number:'))
List = [item + 1 for item in range(m)]
sort_print(List, 0, m)


参数List存储n个不同元素,参数start指定待排列元素的首元素位置。
n-start为问题的规模,初始时,start=0,问题的规模为n,接下来规模依次递减1
根据sort_print(List,start+1)建立时间递推关系,设T(n)表示规模为n的耗时,则规模为n-1的耗时为T(n-1),进入递归之前需要交换两个元素,递归回来之后又需要交换两个元素,耗时为常数O(1),递归和交换元素需要做n-start次,初始start=0,故循环n次。该语句的递推式为:T(n)=n(T(n-1)+O(1))。
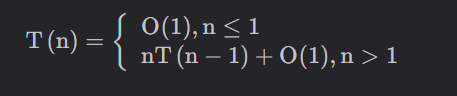
采用迭代法递推:
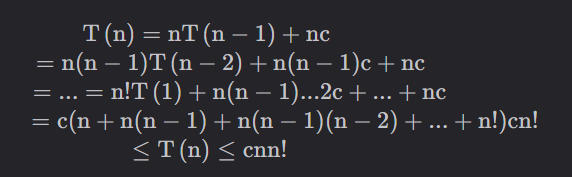
因此结果时间复杂度为O(n!)
3.4 实验总结
此次实验室求给定数字的全排列,我们考虑利用递归的方法进行算法的实现,即N个数,只要前面N-1个数字已经生成的全排列,只用将N插入到这些排列中,生成新的排列顺序。
Karatsuba乘法是一种快速乘法。此算法在1960年由Anatolii Alexeevitch Karatsuba 提出,并于1962年得以发表。此算法主要用于两个大数相乘。普通乘法的复杂度是n^2,而Karatsuba算法的复杂度仅为3nlog3≈3n1.585(log3是以2为底的)。
算法介绍:

实例展示:

给定两个两个n*n矩阵,求他们的乘积,如下所示:
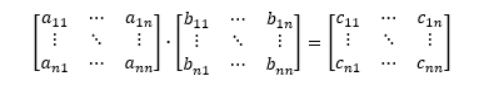
分块进行乘法

简单分治:
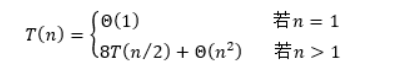
T(n) = O(n^2)
Strassen算法:只需要递归7次,而非8次
(1) 将输入矩阵A、B以及输出矩阵C各分解为4个(n/2)×(n/2)子矩阵。
(2) 创建10个(n/2)×(n/2)矩阵S1,S2,…,S10,如下所示。由于需要进行101次(n/2)×(n/2)矩阵的加减法,所以这一步花费Θ(n2))时间。
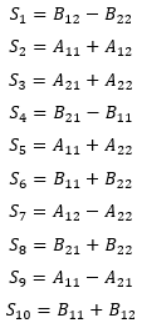
(3) 用步骤(1)分解得到的子矩阵和步骤(2)中创建的10个矩阵,递归地计算7个矩阵乘积P1,P2,…,P7

(4) 利用矩阵P1,P2,…,P7进行加减运算,得到输出矩阵C的子矩阵C11,C12,C21,C22这一步需要进行8次(n/2)×(n/2)矩阵的加减法,所以花费时为Θ(n2)
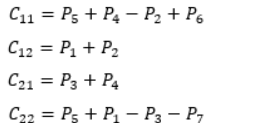

证明:总共有n个元素,每次查找的区间大小就是n,n/2,n/4,…,n/2^k(接下来操作元素的剩余个数),其中k就是循环的次数。
由于n/2^k取整后>=1,即令n/2^k=1,可得k=log2n,(是以2为底,n的对数),所以时间复杂度可以表示O()=O(logn)
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法,归并排序对序列的元素进行逐层折半分组,然后从最小分组开始比较排序,合并成一个大的分组,逐层进行,最终所有的元素都是有序的。
算法原理:
1.时间复杂度
归并排序算法每次将序列折半分组,共需要logn轮,因此归并排序算法的时间复杂度是O(nlogn)
2.空间复杂度
归并排序算法排序过程中需要额外的一个序列去存储排序后的结果,所占空间是n,因此空间复杂度为O(n)
3.稳定性
归并排序算法在排序过程中,相同元素的前后顺序并没有改变,所以归并排序是一种稳定排序算法
快速排序(Quick Sort)是从冒泡排序算法演变而来的,实际上是在冒泡排序基础上的递归分治法。快速排序在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成了两个部分
1.时间复杂度
快速排序算法在分治法的思想下,原数列在每一轮被拆分成两部分,每一部分在下一轮又分别被拆分成两部分,直到不可再分为止,平均情况下需要logn轮,因此快速排序算法的平均时间复杂度是O(nlogn),在极端情况下,快速排序算法每一轮只确定基准元素的位置,时间复杂度为O(N^2)
2.空间复杂度
快速排序算法排序过程中只是使用数组原本的空间进行排序,因此空间复杂度为O(1)
3.稳定性
快速排序算法在排序过程中,可能使相同元素的前后顺序发生改变,所以快速排序是一种不稳定排序算法
相同点:
1.利用分治思想
2.具体实现都用递归
不同点:
1.先分解再合并:归并排序先递归分解到最小粒度,然后从小粒度开始合并排序,自下而上的合并排序;
2.边分解边排序:快速排序每次夯解都实现整体上有序,即参照值左侧的数都小于参照值,右侧的大于参照值;是自上而下的排序;
3.归并排序不是原地排序,因为两个有序数组的合并一定需要额外的空间协助才能合并;
4.快速排序是原地排序,原地排序指的是空间复杂度为O(1);
5.归并排序每次将数组一分为二,快排每次将数组一分为三。