计硕二班 肖泽秋 2022222233 第二章作业

[moodfriend]

一、第二章学习心得

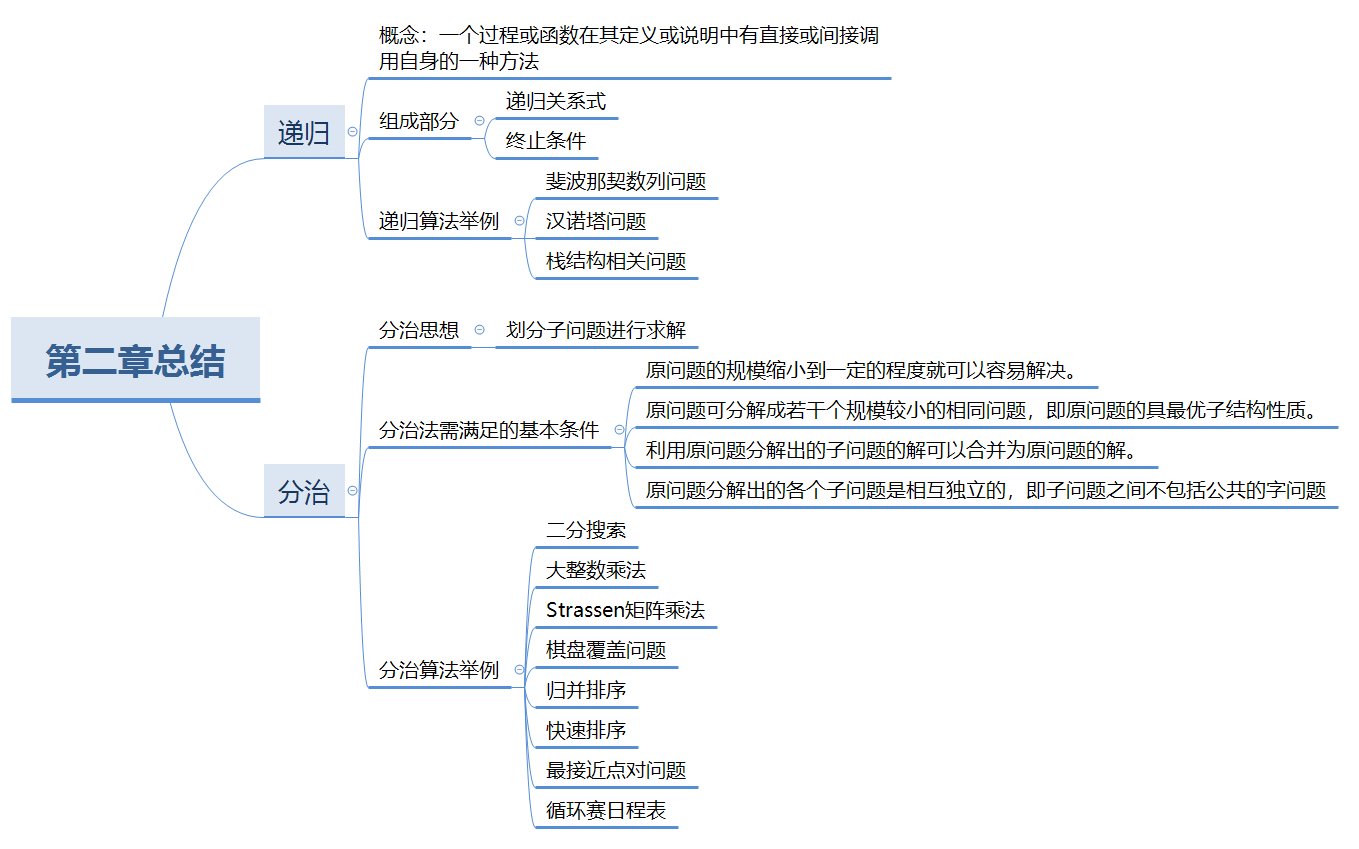
分治算法思想： 规模为n的原问题的解无法解决求出，进行问题规模缩减，划分子问题(子问题相互独立且和原问题的性质相同，只有问题的规模变小)，一直递归划分到子问题可以很简单的求解，最后在将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上求出原问题的解。

分治法使用条件：

1. 原问题的规模缩小到一定的程度就可以容易解决。
2. 原问题可分解成若干个规模较小的相同问题，即原问题的具最优子结构性质。
3. 利用原问题分解出的子问题的解可以合并为原问题的解。
4. 原问题分解出的各个子问题是相互独立的，即子问题之间不包括公共的字问题 (如果各个子问题不独立，则使用动态规划更好)。

二、Fibonacci数列递归算法

Fibonacci数列求解有两种算法，一种是累加循环求和，一种是利用分治思想递归求和，在本章使用分治思想进行求解

求解思路：

根据规律，数列中的数等于前两项的和，所以整个数列的和等于从最后一项一直加到第一项

递归关系式：

 

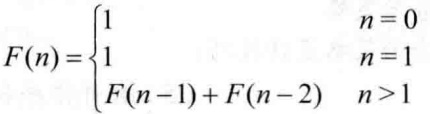
def fibonacci(n):
    """fibonacci数列求解"""
    if n <= 1:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

时间复杂度分析：

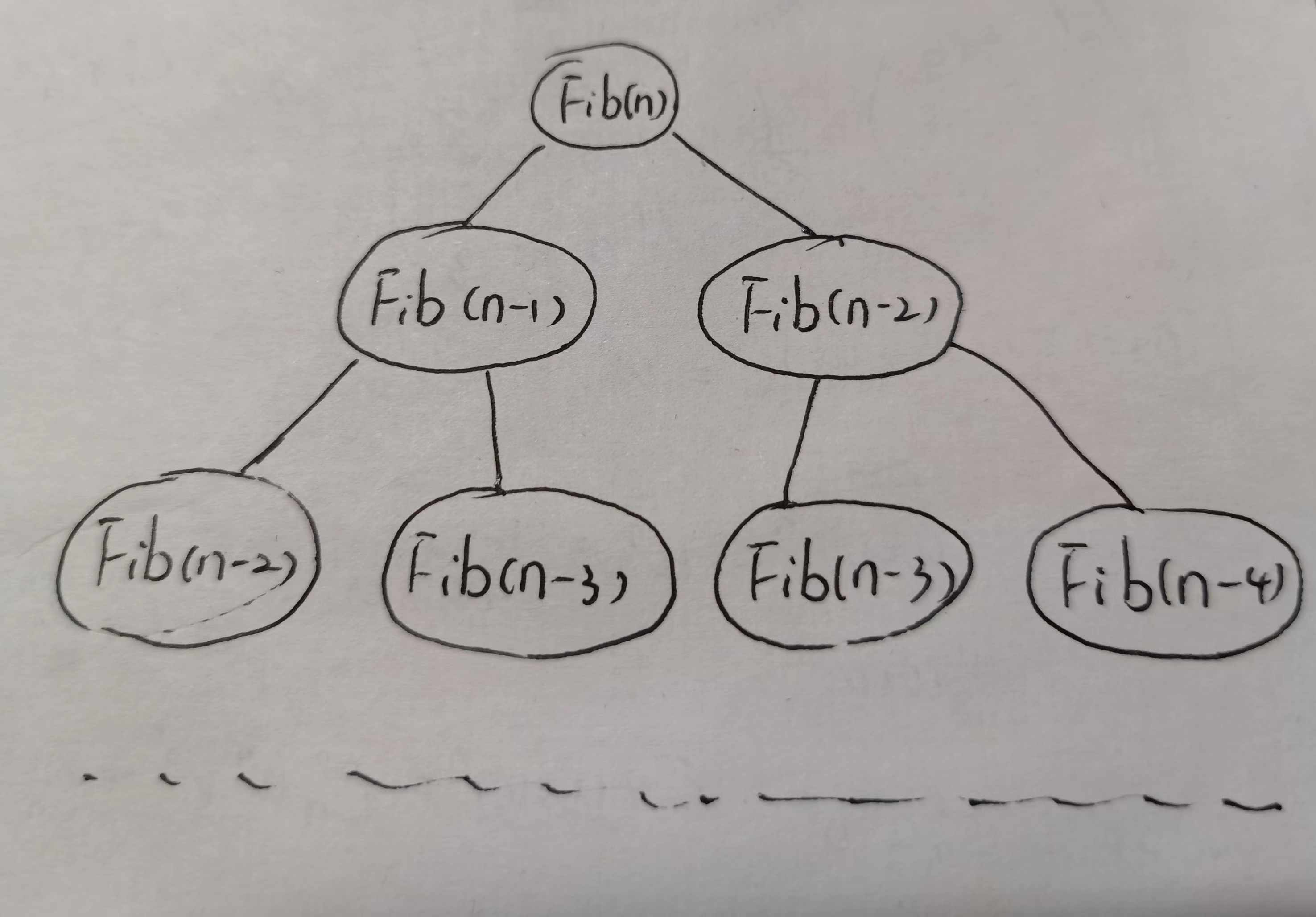
函数递归执行顺序是如图所示的二叉树结构，每个节点即是函数执行的次数

所以时间复杂度T(n) = O(2^(n -  2) + 1) = O (2^n)

三、全排列问题

思路：假设只有1、2、3三个数字，我们该把2加入，显然可以有两种方式，一种是插入到1之前，另一种是插入到1之后，也就是插空，得到[1,2]，[2,1]，同理，下面插入3，显然，对于[1,2]，有三个空，把3分别插入，也就得到三种，对于[2,1]，也有三个空，把3分别插入，也得到三种。当然，这两大种情况一定不会重复，因为1和2的位置(先后顺序)是不同的。这样我们得到了由一个元素，两个元素，三个元素分别形成的全排列。

def permute(nums):
    length = len(nums)
    result = [[[nums[0]]]]
    if length == 1:
        return result[0]
    else:
        for i in range(1, length):
            result.append(list())
            for j in result[i - 1]:
                for k in range(len(j) + 1):
                    j.insert(k, nums[i])
                    result[i].append(list(j))
                    j.pop(k)

    return result[length - 1]


if __name__ == '__main__':
    n = int(input())
    my_list = [i for i in range(1, n + 1)]
    res = permute(my_list)
    for r in res:
        for i in r:
            print(i, end='')
        print()

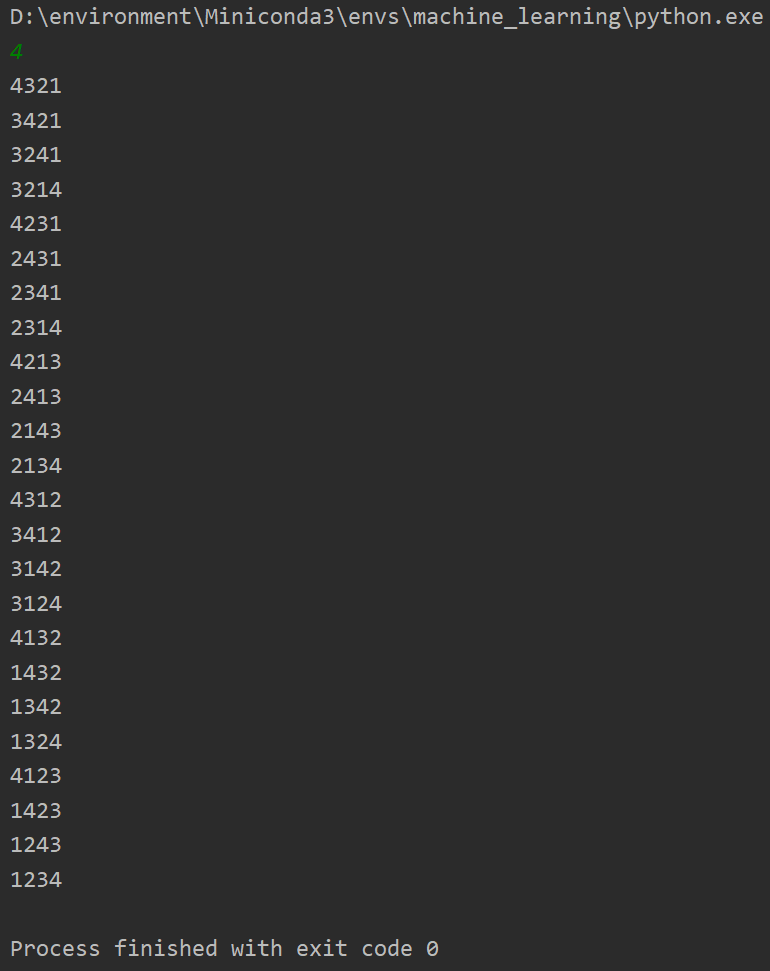
时间复杂度分析：

计算排列情况的时候有三层循环，首先是计算长度，再是对列表中的元素遍历进行插入，所以时间复杂度为O(n^3)

四、Karatsuba’s 大整数乘法、Strassen矩阵乘法分治策略应用特点

Karatsuba’s 大整数乘法

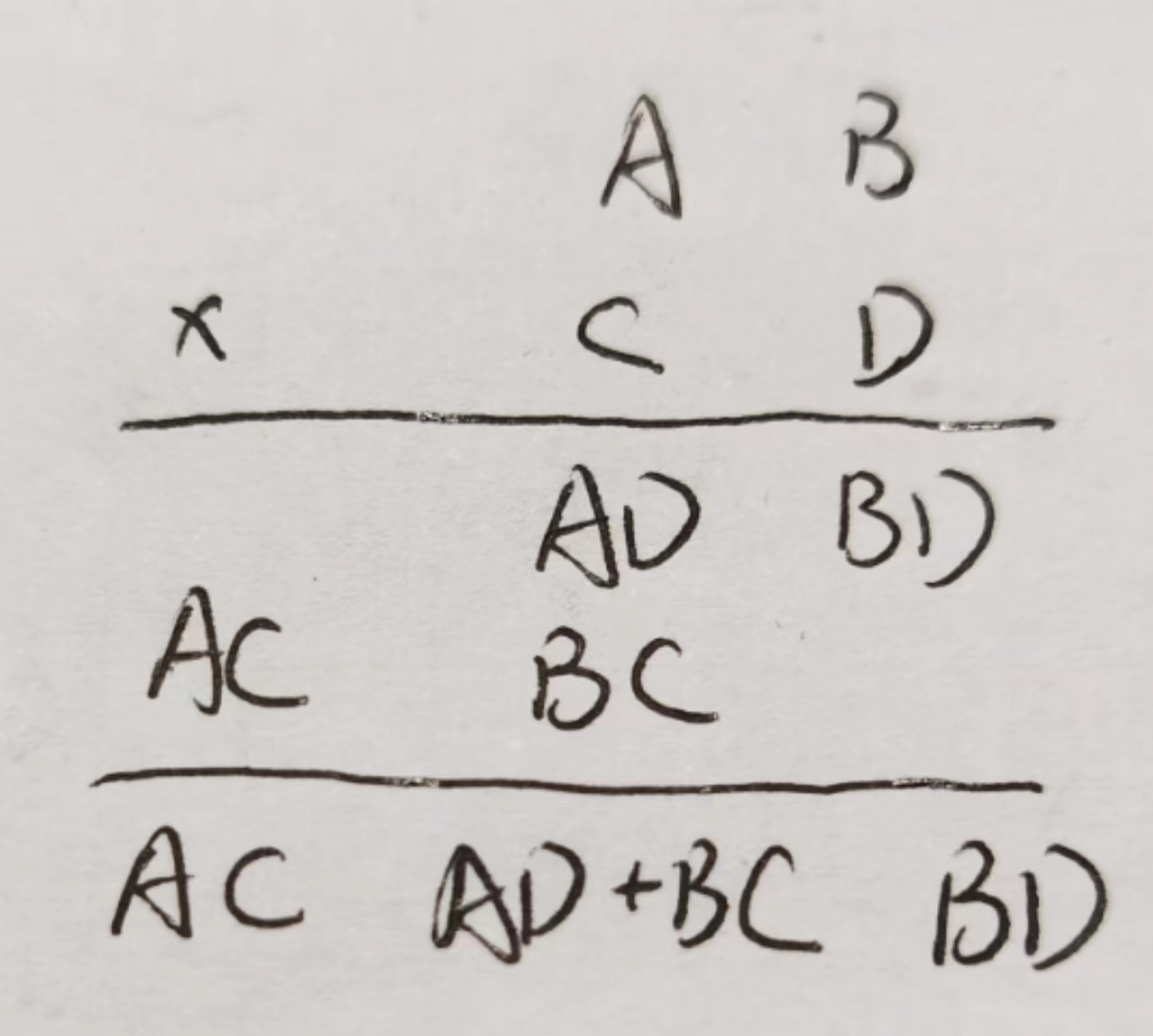
 大整数乘法原理是将大数分成两段后变成较小的数位，然后做3次乘法

主要步骤有两步：

1. 分解。将大整数X、Y（分别为n,m位）分别为A、B、C、D。值得注意的是如果位数n或m为奇数，则A为前n/2+1或m/2+1位，n/2或m/2向下取整；

2. 计算。分别计算AC、BD，并且利用AC和BD计算AD+BC。

 

Strassen矩阵乘法

两个大小为 2 * 2 的矩阵相乘，一般需要进行 8 次乘法。而Strassen矩阵乘法可以减少一次乘法，只需要 7 次，在数据量很大的情况能够有效减少矩阵乘法运算的时间。

普通矩阵乘法示意图：

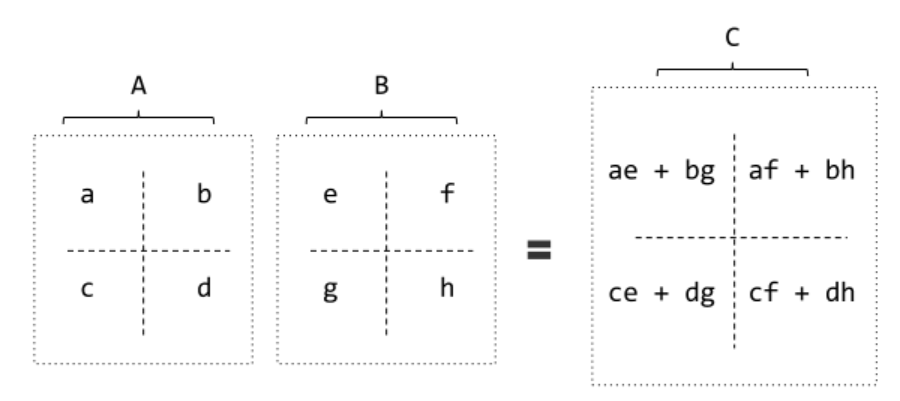
Strassen矩阵乘法示意图：

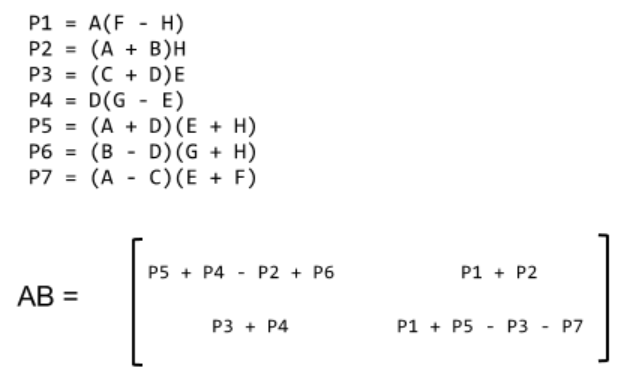
 对比普通的矩阵相乘，这种矩阵相乘运用了递归分治的策略，其递归表达式为：

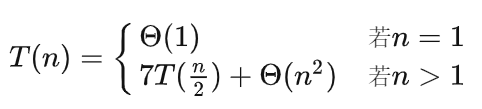
计算时间复杂度为O(log7n/2)

五、二分搜索算法时间复杂度

二分搜索算法是分治思想的典型应用,以一组需要查找的数组为例：

假使需要搜索的元素总共有n个，那么二分后每次查找的区间大小就是n，n/2，n/4，…，n/2^k（接下来操作元素的剩余个数），其中k就是循环的次数。
最坏的情况是K次二分之后,每个区间的大小为1

n/(2^K)肯定是大于等于1，也就是N/(2^K)>=1，计算时间复杂度是按照最坏的情况进行计算，也就是是查到剩余最后一个数才查到我们想要的数据，也就是

n/(2^K)=1

=>n=2^k
可得k=log2n,（是以2为底，n的对数），所以时间复杂度可以表示T(n)=O(logn)

六、排序算法异同

相同点

1. 两个排序算法都体现了分治算法的思想；
2. 具体实现都是通过递归调用实现的。

不同点

1. 从占用的空间来说，归并排序使用了额外的空间，其空间复杂度为O(n)，而快速排序是原地排序，其空间复杂度为O(1)；
2. 从排序过程上来说，归并排序是先将整体元素分成很多单个元素，再进行合并，而快速排序则是先合再分。