计硕三班 李天桢 2022222258 第三章作业

[dzpeople]

1. 概括第三章学习内容，总结第三章学习心得

学习内容

        动态规划算法与分治法类似，其基本思想是将待求解问题分解成若干子问题，先求解子问题，再结合这些子问题的解得到原问题的解。与分治法不同的是，适合用动态规划法求解的问题经分解得到的子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，以致最后解决原问题需要耗费指数级时间。然而，不同子问题的数目常常只有多项式量级。在用分治法求解时，有些子问题被重复计算了许多次。如果能够保存已解决的子问题的答案，在需要时再找出已求得的答案，这样可以避免大量的重复计算，从而得到多项式时间算法。为了达到此目的，可以用一个表来记录所有已解决的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思想。

         具体的动态规划算法多种多样，但它们具有相同的填表格式。动态规划算法适用于解最优化问题，通常可按以下 4 个步骤设计:①找出最优解的性质，并刻画其结构特征;② 递归地定义最优值;③以自底向上的方式计算最优值；④根据计算最优值时得到的信息，构造最优解。
        步骤①~③是动态规划算法的基本步骤。在只需要求出最优值的情形下，步骤④可以省略若需要求出问题的最优解，则必须执行步骤④。此时，在步骤③中计算最优值时，通常需记录更多的信息，以便在步骤④中，根据所记录的信息，快速构造出一个最优解。

学习心得

        对于一个问题还是比较容易确定是否采用动态规划的，因为它是用来求最优值的，一旦题目中有和最优相关的词语就得考虑一下它了（虽然不一定用）。假如做过的题多了，根据经验是比较容易确定的。但是动态规划定义虽然简单，用起来却是另一回事。写代码从来不是解决一个问题的核心，假如有了思路，这里还是很容易解决的。最近做的几道也有了点收获。就像前面说的，dp是自下而上的，所以开始要赋好值。还有，dp是有计算次序的（例如最大矩阵连乘积等问题中，刚开始解决的是相邻元素的合并情况）所以在循环变量有时要特殊处理一下。dp确定的数组一般有特殊意义这点是有利于编程的。

2. 以{0-1}背包问题的动态规划算法设计为例，陈述对伪多项式时间复杂度概念的理解

背包算法的运行时间受输入大小n和背包大小w的限制，同时也受O（nw）的限制，O（nw）的大小呈指数关系。在计算机中以二进制2 ^ n表示。计算复杂性（仅与输入的大小有关，而与它们的大小/值无关。

多项式时间算法：算法的复杂度与输入的规模呈多项式关系。

 伪多项式时间算法：算法的复杂度与输入规模呈指数关系，与输入的数值大小呈多项式关系。

暂时忽略值/重量列表。假设我们有一个背包容量为2的实例。W将在输入数据中占用两位。现在，我们将背包容量增加到4，保留其余输入。我们的输入仅增加了一点，但是计算复杂度却增加了两倍。如果将容量增加到1024，则W的输入将只有10位，而不是2位，但是复杂度增加了512倍。时间复杂度以二进制（或十进制）表示的W大小呈指数增长。

3.算法实验1：采用动态规划算法计算任意两个字符序列的最长公共子序列；总结实验出现问题及解决方法。

def longshort(A, B):
    lenA = len(A)
    lenB = len(B)
    c = [[0 for i in range(lenB + 1)] for j in range(lenA + 1)]
    flag = [[0 for i in range(lenB + 1)] for j in range(lenA + 1)]
    for i in range(lenA):
        for j in range(lenB):
            if a[i] == b[j]:
                c[i + 1][j + 1] = c[i][j] + 1
                flag[i + 1][j + 1] = 'ok'
            elif c[i + 1][j] > c[i][j + 1]:
                c[i + 1][j + 1] = c[i + 1][j]
                flag[i + 1][j + 1] = 'left'
            else:
                c[i + 1][j + 1] = c[i][j + 1]
                flag[i + 1][j + 1] = 'up'
    return c, flag


def printlongshort(flag, a, i, j):
    if i == 0 or j == 0:
        return
    if flag[i][j] == 'ok':
        printlongshort(flag, a, i - 1, j - 1)
        print(a[i - 1], end='')
    elif flag[i][j] == 'left':
        printlongshort(flag, a, i, j - 1)
    else:
        printlongshort(flag, a, i - 1, j)


a = 'ADCBACCDB'
b = 'ABCDADACB'
c, flag = longshort(a, b)
printlongshort(flag, a, len(a), len(b))
print('')

结果：

4.算法实验2：利用动态规划算法编程求解矩阵连乘问题；总结实验出现问题及解决方法。 

N = 9
p = [2, 3, 54, 52, 210, 120, 154,34,13]
m = [[0 for _ in range(0, N)] for _ in range(0, N)]
s = [[0 for _ in range(0, N)] for _ in range(0, N)]


def Series(n):
    for r in range(2, n + 1):
        for i in range(1, n - r + 2):
            j = i + r - 1
            m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j]
            s[i][j] = i
            for k in range(i + 1, j):
                t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j]
                if t < m[i][j]:
                    m[i][j] = t
                    s[i][j] = k


def count(i, j):
    if i == j:
        print('A[', i, ']', end=' ')
        return
    print('(', end=' ')
    count(i, s[i][j])
    count(s[i][j] + 1, j)  # 递归1到s[1][j]
    print(')', end=' ')


if __name__ == '__main__':
    Series(N - 1)
    for i in m[1:]:
        print(i[1:])
    count(1, N - 1)

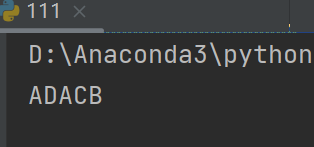
结果：