计硕3班孙志州-2022222274-第四章作业

tssq2009 2022-12-30 13:17:18

算法设计与分析第四章作业

1. 概括第四章学习内容，总结第四章学习心得。

第四章集中学习了贪心算法相关知识。主要学习内容如下图所示：

在本章知识中，求解最优解问题过程中，经常遇到贪心算法与动态规划算法有相互混淆的现象，通过本章对贪心算法的特点以及问题解特征的学习，更进一步掌握了这些问题。

2. 以{0-1}背包问题和背包问题为例，讨论动态规划算法与贪心算法的异同。

0-1背包问题：

给定n种物品和一背包。物品i的重量是wi，其价值为bi，背包容量为w。问如何选择装入背包的物品使得装入背包的物品总价值最大? (wi, bi和 w 都是整数)

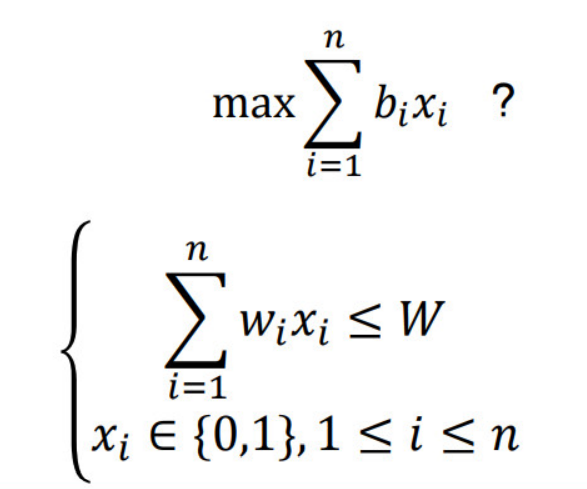
由0-1背包问题的最优子结构性质，可以建立计算B(k，w)的递归式如下:

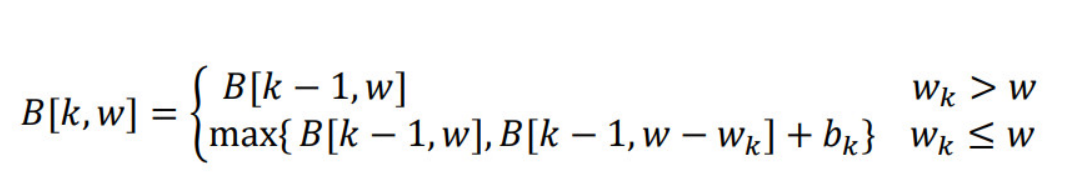
算法描述为：

Knapsack(int n, bll,wll.W)
{
boolean x[]; 
int B[n][W];
for (int w = 0; w<=W; w++) B[0,w] = 0;
for (int i = 1; i<=n; i++) {
B[i,0] = 0;
for (int w = 1; w<=W; w++){
if (w[i] <= w){ 
if (b[i] + B[i-1,w-w] > B[i-1,w]{
B[i,w] = b[i] + B[i-l,w- w[i]];
}
else{ B[i,w] = B[i-l,w]; }
else {B[i],w] = B[i-1,w]; } 
}
}
}

背包问题

与0-1背包问题类似，所不同的是在选择物品i装入背包时，可以选择物品i的一部分，而不一定要全部装入背包，1<i<n。

这2类问题都具有最优子结构性质，极为相似，但背包问题可用贪心算法求解得到最优解，0-1背包问题却不能用贪心算法求解。

其算法描述为：

GREEDY-KNAPSACK(valueln],weight[n],C)
{float x(nl, LW;
Sort(value[n]/weightn]);
for(i=1;i<=n;i++) x[i]=0;
LW=C;
i=1;
while(weight[i]<=LW){
x[i]=1;
LW=LW-weight[i];
i++;
}
x[i]= LW/ weight[i];;
}

贪心算法与动态规划算法的差异

共同点:所求解的问题具有最优子结构性质。

问题1:具有最优子结构的问题应该选用贪心算法还是动态规划算法求解?

问题2:能用动态规划算法求解的问题是否也能用贪心算法求解?

背包问题实例:贪心算法与动态规划算法的区别。

3. 算法实验2：完成教材114页算法实现题4-2，总结实验出现问题及解决方法。

#include <bits/stdc++.h>
  using namespace std;
  bool cmp(int a, int b){
    return a>b;
 }
 
 int main(){
 int k;
int a[1000], b[1000];
int Min = 0, Max = 0;
cin>>k;
for(int i=0; i<k; i++){
    cin>>a[i];
    b[i]= a[i];
   }
  sort(a, a+k);
  sort(b, b+k, cmp);
  for(int i=0; i<k-1; i++){
a[i+1] = a[i]+a[i+1];
Min += a[i+1];
sort(a+i+1, a+k);

b[i+1] = b[i]+b[i+1];
        Max += b[i+1];
  sort(b+i+1, b+k ,cmp);
  }
cout<<Max-k+1<<' '<<Min-k+1<<endl;
  return 0;
}

4. 算法实验2：完成教材118页算法实现题4-14，总结实验出现问题及解决方法。

#include <bits/stdc++.h>
int main()
{
int n,k; 
int numx;  
    long long min=0,max=0; 
    priority_queue<int, vector<int>, greater<int> > qc;   
    priority_queue<int, vector<int>, less<int> > qd;
    cin>>n>>k;
    for(int i=0;i<n;i++)  
    {
        cin>>numx;
        qc.push(numx);
        qd.push(numx);
    }
    while(qc.size()%(k-1)!=1)  
        qc.push(0);  
    while(qc.size()>1)
    {
        long long sum=0;
        for(int i=0;i<k;i++)   
        {
            sum+=qc.top();
            qc.pop();  
        }
        min+=sum;  
        qc.push(sum); 
    }
 
    while(qd.size()>1)
    {
        long long sum=0;
        for(int i=0;i<2;i++)
        {
             sum+=qd.top();
             qd.pop();
        }
        max+=sum;
        qd.push(sum);
    }
    cout<<max<<" "<<min<<endl;
    return 0;
}

...全文