145
社区成员
发帖
与我相关
我的任务
分享计硕3班-郭兴君-2022222279-第三章作业
1、学习内容总结和心得体会
1.1 动态规划算法
动态规划法将待求解问题分解成若干个相互重叠的子问题，每个子问题对应问题求解过程的一个阶段，在各阶段子问题求解中，计算子问题的解并填入表中，当下一阶段需要再次计算此问题时，可以通过查表获得该子问题的船而不用再次求解，从而避免了大量重复计算。动态规划法利用最优决策表保存已解决子问题的答案，在计算其他子问题，若需要使用已解决子问题解时，只需从决策表找出已求答案，以避免大量重复计算，改善算法效率。
动态规划的四个步骤：
(1)分析问题的最优解结构;
(2) 递归的定义最优值: 分析问题是否满足最优性原理，找出动态规划函数的递归式;
(3) 构造算法求解: 以递推计算各个子问题的最优值，逐步构造出整个问题的最优值;
(4) 根据计算最优值时得到的信息，以 (3) 中的相反方向构造最优解。
1.2 最优化问题
有n个输入，问题解经由n个输入的一个子集组成，这个子集必须满足某些事先给定的条件，这些条件称为约束条件。满足约束条件的解称为问题的可行解。满足约束条件的可行解不唯一，使得判别优劣的目标函数取得极值的可行解成为最优解。这一类问题就是最优化问题。
1.3 动态规划问题实例
（1）0-1背包问题
(2) 最长公共子序列问题
(3) 矩阵连乘问题
1.4 学习心得
动态规划就是我从初学开始遇到的最神奇的解法，它不同于暴力搜索，也不同于一般的贪心，能够以出乎人意料的时间复杂度（近似于O（n^2））解决一些难题，算法远远优于一般的深搜（O（2^n））。不过，动态规划的思维性比较强，必须会设好状态，正确写出状态转移方程，并且能够准确判断有无最优子结构。
其实有点像贪心，但是它有局部最优解推导向整体最优解的过程，形象一点说，动态规划的“眼光”比贪心更长远，有一个更新最优解的过程，发现问题了可以“反悔”。它还有一点分治的味道，通过对问题划分各个阶段，对各个阶段分别求解，最后推向整体的过程。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。
学习动态规划是一个比较漫长的过程，需要慢慢领悟，去体会动态规划的奥义。显然，多做题，多思考是必需的，坚持下去，慢慢就能学会了。
2.以{0-1}背包问题的动态规划算法设计为例，陈述对伪多项式时间复杂度概念的理解
2.1 0-1背包问题
{0-1}背包问题：背包大小为w，物品个数为n，每个物品的重量与价值分别对应的 w[i]与 v[i]，要求使得放入背包中物品的总价值最大。如果 对于第 i 个物品放入背包后价值量最大，则前 i-1 个物品在背包容量为 w-w[i] 的情况下能够取到最大的价值。因为第 i 个物品可以放入，对应要占用背包 w[i] 的容量，所以 w-w[i] 的背包容量就是前 i-1 个物品所共有的总容量。因此需要搞懂三点知识点，
1.0-1背包问题中最重要的点是弄清楚背包容量是多少，物品是哪些
2.其次，我们要注意遍历顺序为先遍历物品后遍历背包容量
3.最后，我们要注意要统计的是有关最大价值类问题还是组合数的问题。
2.2 伪多项式理解
如果一个算法的传统时间复杂度是多项式时间的，而标准时间复杂度不是多项式时间的，则我们称这个算法是伪多项式时间的。当一个算法的最坏时间复杂度是依据输入的数量级的时候，我们就称算法的时间复杂度是伪多项式时间。若一个数值算法的时间复杂度可以表示为输入数值规模N的多项式，但其运行时间与输入数值规模N的二进制位数呈指数增长关系，则称其时间复杂度为伪多项式时间复杂度。这是由于N的值是N的位数的幂，故该算法的时间复杂度实际上应视为输入数值N的位数的幂。
3. 算法实验1：采用动态规划算法计算任意两个字符序列的最长公共子序列；总结实验出现问题及解决方法
3.1问题分析
设序列X={x1,x2,...,xm}和Y={y1,y2,...yn}的最长公共子序列为Z={z1,z2,...zk}，则
（1）若xm=yn，则zk=xm=yn，且Zk-1是Xm-1和Yn-1的最长公共子序列；
（2）若xm≠yn且zk≠xm，则Z是Xm-1和Y的最长公共子序列；
（3）若xm≠yn且zk≠yn，则Z是X和Yn-1的最长公共子序列；
引入二维表c，用c[i][j]记录序列Xi和Yj的最长公共子序列的长度，其中Xi={x1,x2,...,xi},Yj={y1,y2,...yj}
可建立递归关系如下：
3.2 过程分析
（1）步骤一：最长公共子序列问题的最优子结构；
（2）步骤二：定义求解问题最优值的递归结构；
（3）步骤三：计算最优值；
（4）步骤四：构造最优解。
3.3 代码求解
#include <iostream>
#include <string>
#include <stack>
using namespace std;
void LCS(string s1,string s2)
{
int m=s1.length()+1;
int n=s2.length()+1;
int **c;
int **b;
c=new int* [m];
b=new int* [m];
for(int i=0;i<m;i++)
{
c[i]=new int [n];
b[i]=new int [n];
for(int j=0;j<n;j++)
b[i][j]=0;
}
for(int i=0;i<m;i++)
c[i][0]=0;
for(int i=0;i<n;i++)
c[0][i]=0;
for(int i=0;i<m-1;i++)
{
for(int j=0;j<n-1;j++)
{
if(s1[i]==s2[j])
{
c[i+1][j+1]=c[i][j]+1;
b[i+1][j+1]=1; //1表示箭头为 左上
}
else if(c[i][j+1]>=c[i+1][j])
{
c[i+1][j+1]=c[i][j+1];
b[i+1][j+1]=2; //2表示箭头向 上
}
else
{
c[i+1][j+1]=c[i+1][j];
b[i+1][j+1]=3; //3表示箭头向 左
}
}
}
for(int i=0;i<m;i++) //输出c数组
{
for(int j=0;j<n;j++)
{
cout<<c[i][j]<<' ';
}
cout<<endl;
}
stack<char> same; //存LCS字符
stack<int> same1,same2; //存LCS字符在字符串1和字符串2中对应的下标，方便显示出来
for(int i = m-1,j = n-1;i >= 0 && j >= 0; )
{
if(b[i][j] == 1)
{
i--;
j--;
same.push(s1[i]);
same1.push(i);
same2.push(j);
}
else if(b[i][j] == 2)
i--;
else
j--;
}
cout<<s1<<endl; //输出字符串1
for(int i=0;i<m && !same1.empty();i++) //输出字符串1的标记
{
if(i==same1.top())
{
cout<<1;
same1.pop();
}
else
cout<<' ';
}
cout<<endl<<s2<<endl; //输出字符串2
for(int i=0;i<n && !same2.empty();i++) //输出字符串2的标记
{
if(i==same2.top())
{
cout<<1;
same2.pop();
}
else
cout<<' ';
}
cout<<endl<<"最长公共子序列为：";
while(!same.empty())
{
cout<<same.top();
same.pop();
}
cout<<endl<<"长度为："<<c[m-1][n-1]<<endl;
for (int i = 0; i<m; i++)
{
delete [] c[i];
delete [] b[i];
}
delete []c;
delete []b;
}
int main()
{
string s1="ABCPDSFJGODIHJOFDIUSHGD";
string s2="OSDIHGKODGHBLKSJBHKAGHI";
LCS(s1,s2);
return 0;
}
3.4 问题及解决方式
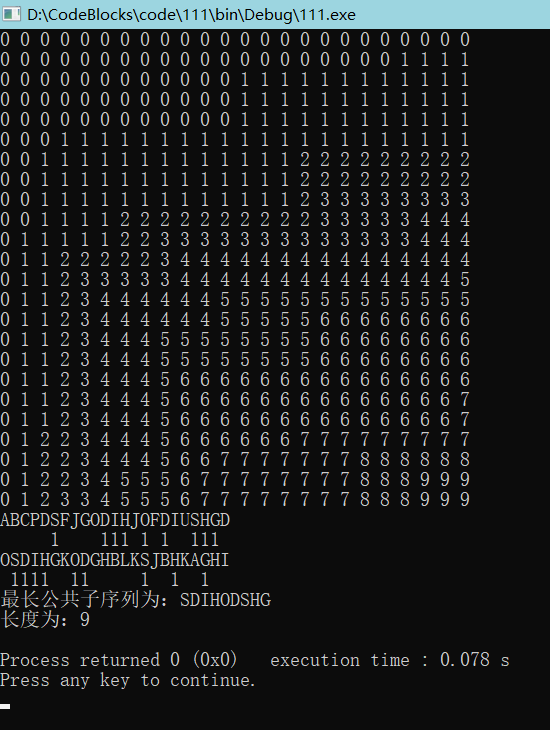
此，我们只需要从c[0][0]开始填表，填到c[m-1][n-1]，所得到的c[m-1][n-1]就是LCS的长度
但是，我们怎么得到LCS本身而非LCS的长度呢？
也是用一个二维数组b来表示：
在对应字符相等的时候，用↖标记
在p1 >= p2的时候，用↑标记
在p1 < p2的时候，用←标记
若想得到LCS，则再遍历一次b数组就好了，从最后一个位置开始往前遍历：
如果箭头是↖，则代表这个字符是LCS的一员，存下来后 i-- , j--
如果箭头是←，则代表这个字符不是LCS的一员，j--
如果箭头是↑ ，也代表这个字符不是LCS的一员，i--
如此直到i = 0或者j = 0时停止，最后存下来的字符就是所有的LCS字符
4. 算法实验2：利用动态规划算法编程求解矩阵连乘问题；总结实验出现问题及解决方法
4.1 问题分析
由于矩阵乘法满足结合律，故计算矩阵的连乘积可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
完全加括号的矩阵连乘积可递归地定义为：
（1）单个矩阵是完全加括号的；
（2）矩阵连乘积A是完全加括号的，则A可表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号，即A=(BC)
例如，矩阵连乘积A1A2A3A4有5种不同的完全加括号的方式：(A1(A2(A3A4)))，(A1((A2A3)A4))，((A1A2)(A3A4))，((A1(A2A3))A4)，(((A1A2)A3)A4)。每一种完全加括号的方式对应于一个矩阵连乘积的计算次序，这决定着作乘积所需要的计算量。
看下面一个例子，计算三个矩阵连乘{A1，A2，A3}；维数分别为10*100 , 100*5 , 5*50 按此顺序计算需要的次数((A1*A2)*A3):10X100X5+10X5X50=7500次，按此顺序计算需要的次数(A1*(A2*A3)):10*5*50+10*100*50=52500次
所以问题是：如何确定运算顺序，可以使计算量达到最小化。
4.2 设计思路
例：设要计算矩阵连乘乘积A1A2A3A4A5A6，其中各矩阵的维数分别是：
A1：30*35; A2：35*15; A3：15*5; A4：5*10; A5：10*20; A6：20*25
4.3 建立递推关系
设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为m[1,n]。
当i=j时，A[i:j]=Ai，因此，m[i][i]=0，i=1,2,…,n
当i<j时，若A[i:j]的最优次序在Ak和Ak+1之间断开，i<=k<j,则：m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置，所以k还未定。不过k的位置只有j-i个可能。因此，k是这j-i个位置使计算量达到最小的那个位置。
综上，有递推关系如下：
4.4 构建最优解
若将对应m[i][j]的断开位置k记为s[i][j]，在计算出最优值m[i][j]后，可递归地由s[i][j]构造出相应的最优解。s[i][j]中的数表明，计算矩阵链A[i:j]的最佳方式应在矩阵Ak和Ak+1之间断开，即最优的加括号方式应为(A[i:k])(A[k+1:j)。因此，从s[1][n]记录的信息可知计算A[1:n]的最优加括号方式为(A[1:s[1][n]])(A[s[1][n]+1:n])，进一步递推，A[1:s[1][n]]的最优加括号方式为(A[1:s[1][s[1][n]]])(A[s[1][s[1][n]]+1:s[1][s[1][n]]])。同理可以确定A[s[1][n]+1:n]的最优加括号方式在s[s[1][n]+1][n]处断开...照此递推下去，最终可以确定A[1:n]的最优完全加括号方式，及构造出问题的一个最优解。
4.5 算法代码
#include<iostream>
using namespace std;
const int N = 100;
int A[N];//矩阵规模
int m[N][N];//最优解
int s[N][N];
void MatrixChain(int n)
{
int r, i, j, k;
for (i = 0; i <= n; i++)//初始化对角线
{
m[i][i] = 0;
}
for (r = 2; r <= n; r++)//r个矩阵连乘
{
for (i = 1; i <= n - r + 1; i++)//r个矩阵的r-1个空隙中依次测试最优点
{
j = i + r - 1;
m[i][j] = m[i][i]+m[i + 1][j] + A[i - 1] * A[i] * A[j];
s[i][j] = i;
for (k = i + 1; k < j; k++)//变换分隔位置，逐一测试
{
int t = m[i][k] + m[k + 1][j] + A[i - 1] * A[k] * A[j];
if (t < m[i][j])//如果变换后的位置更优，则替换原来的分隔方法。
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
void print(int i, int j)
{
if (i == j)
{
cout << "A[" << i << "]";
return;
}
cout << "(";
print(i, s[i][j]);
print(s[i][j] + 1, j);//递归1到s[1][j]
cout << ")";
}
int main()
{
int n;//n个矩阵
cin >> n;
int i, j;
for (i = 0; i <= n; i++)
{
cin >> A[i];
}
MatrixChain(n);
cout << "最佳添加括号的方式为：";
print(1, n);
cout << "\n最小计算量的值为：" << m[1][n] << endl;
return 0;
}
4.6 实验出现问题及解决方法
暂无
...全文
请发表友善的回复…
发表回复
