144
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享目录
第三章 动态规划法
二、算法实验1:采用动态规划算法计算任意两个字符序列的最长公共子序列
与分治法类似,动态规划算法的基本思想也是将待求解问题分解成若干个子问题,但是经分解得到的子问题往往不是互相独立的。
若用分治方法解决这类问题,将重复计算公共子问题,效率很低,甚至在求解多项式量级的子问题数目时也可能耗费指数时间。由于动态规划法用表保存已解决子问题的答案,需要时再找出已求得的答案,就可以避免大量重复计算,从而提高算法效率。
最优化问题是动态规划求解的一类典型问题。
有n个输入,问题解经由n个输入的一个子集组成,这个子集必须满足某些事先给定的条件,这些条件称为约束条件。
满足约束条件的解称为问题的可行解。满足约束条件的可行解不唯一,使得判别优劣的目标函数取得极值的可行解成为最优解。这一类问题就是最优化问题。
基本要素:
一、最优子结构
注意:同一个问题可以有多种方式刻划它的最优子结构。
二、重叠子问题
![]()
步骤:
给定n种物品和一背包。物品i 的重量是wi ,其价值为bi ,背包容量为W 。问如何选择装入背包的物品,使得装入背包的物品总价值最大?(wi, bi 和W 都是整数)
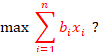
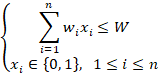

若给定序列![]() ,则另一序列
,则另一序列![]() 是X 的子序列是指,存在一个严格递增下标序列
是X 的子序列是指,存在一个严格递增下标序列![]() 使得对于所有j
使得对于所有j![]() 有:
有:![]() 。
。
例如:序列![]() 是序列
是序列![]() 的一个子序列,相应的递增下标序列为
的一个子序列,相应的递增下标序列为![]() 。
。
给定2个序列X和Y,另一序列Z 既是X 的子序列又是Y 的子序列时,称Z 是序列X 和Y 的公共子序列。
给定2个序列![]() 和
和![]() ,找出X 和Y 的最长公共子序列。
,找出X 和Y 的最长公共子序列。
子问题最优值的递归结构:
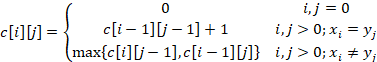
LCS问题中数据结构的设计:
二维数组![]() ,其中m 为序列X 的长度,n 为序列Y 的长度。数组元素
,其中m 为序列X 的长度,n 为序列Y 的长度。数组元素![]() 用于存储子序列
用于存储子序列![]() 和
和![]() 的LCS长度;
的LCS长度;![]() 用于记录
用于记录![]() 的值是哪个子问题的解产生。
的值是哪个子问题的解产生。
规定:
1、子问题:若![]() ,则
,则![]()
2、子问题:若![]() 且
且![]() ,则
,则![]()
3、子问题:若![]() 且
且![]() ,则
,则![]()
#include <iostream>
#include <string>
#include <stack>
using namespace std;
void LCS(string s1,string s2)
{
int m=s1.length()+1;
int n=s2.length()+1;
int **c;
int **b;
c=new int* [m];
b=new int* [m];
for(int i=0;i<m;i++)
{
c[i]=new int [n];
b[i]=new int [n];
for(int j=0;j<n;j++)
b[i][j]=0;
}
for(int i=0;i<m;i++)
c[i][0]=0;
for(int i=0;i<n;i++)
c[0][i]=0;
for(int i=0;i<m-1;i++)
{
for(int j=0;j<n-1;j++)
{
if(s1[i]==s2[j])
{
c[i+1][j+1]=c[i][j]+1;
b[i+1][j+1]=1;
}
else if(c[i][j+1]>=c[i+1][j])
{
c[i+1][j+1]=c[i][j+1];
b[i+1][j+1]=2;
}
else
{
c[i+1][j+1]=c[i+1][j];
b[i+1][j+1]=3;
}
}
}
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
cout<<c[i][j]<<' ';
}
cout<<endl;
}
stack<char> same;
stack<int> same1,same2;
for(int i = m-1,j = n-1;i >= 0 && j >= 0; )
{
if(b[i][j] == 1)
{
i--;
j--;
same.push(s1[i]);
same1.push(i);
same2.push(j);
}
else if(b[i][j] == 2)
i--;
else
j--;
}
cout<<s1<<endl;
for(int i=0;i<m && !same1.empty();i++)
{
if(i==same1.top())
{
cout<<1;
same1.pop();
}
else
cout<<' ';
}
cout<<endl<<s2<<endl;
for(int i=0;i<n && !same2.empty();i++)
{
if(i==same2.top())
{
cout<<1;
same2.pop();
}
else
cout<<' ';
}
cout<<endl<<"最长公共子序列为:";
while(!same.empty())
{
cout<<same.top();
same.pop();
}
cout<<endl<<"长度为:"<<c[m-1][n-1]<<endl;
for (int i = 0; i<m; i++)
{
delete [] c[i];
delete [] b[i];
}
delete []c;
delete []b;
}
int main()
{
string s1="ABCPDSFJGODIHJOFDIUSHGD";
string s2="OSDIHGKODGHBLKSJBHKAGHI";
LCS(s1,s2);
return 0;
}
#include<iostream>
using namespace std;
const int N = 100;
int A[N];
int m[N][N];
int s[N][N];
void MatrixChain(int n)
{
int r, i, j, k;
for (i = 0; i <= n; i++)
{
m[i][i] = 0;
}
for (r = 2; r <= n; r++)
{
for (i = 1; i <= n - r + 1; i++)
{
j = i + r - 1;
m[i][j] = m[i][i]+m[i + 1][j] + A[i - 1] * A[i] * A[j];
s[i][j] = i;
for (k = i + 1; k < j; k++)
{
int t = m[i][k] + m[k + 1][j] + A[i - 1] * A[k] * A[j];
if (t < m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
void print(int i, int j)
{
if (i == j)
{
cout << "A[" << i << "]";
return;
}
cout << "(";
print(i, s[i][j]);
print(s[i][j] + 1, j);
cout << ")";
}
int main()
{
int n;
cin >> n;
int i, j;
for (i = 0; i <= n; i++)
{
cin >> A[i];
}
MatrixChain(n);
cout << "最佳添加括号的方式为:";
print(1, n);
cout << "\n最小计算量的值为:" << m[1][n] << endl;
return 0;
}