计硕三班-熊鑫2022222296-第四章作业

HeySkyGirl 2022-12-30 23:32:45

一、概括第四章学习内容，总结第四章学习心得。

二、算法实验1：完成教材114页算法实现题4-2，总结实验出现问题及解决方法。

三、算法实验2：完成教材118页算法实现题4-14，总结实验出现问题及解决方法。

一、概括第四章学习内容，总结第四章学习心得。

1、贪心算法概念

又称贪婪算法，常用于优化问题近似解的求解。
求解过程特点：从问题的初始状态出发，通过若干次贪心选择而得出问题最优解（或较优解）的一种计算机解题方法。
贪心法每次所做出的选择只是在某种意义上的局部最优选择，这种局部最优选择并不总能保证获得问题的整体最优解，但通常能获得近似最优解。
在众多的计算机算法中，贪心策略是最接近人们日常思维的一种解题策略。

2、可采用贪心算法求解问题的特征

（1）最优子结构性质：一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质，也称此问题满足最优性原理。

这是贪心算法可行的第一个基本要素。
最优子结构性质是某问题可用动态规划算法或贪心算法求解的关键特性。

（2）贪心选择性质：贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择（贪心选择）得到。

这是贪心算法可行的第二个基本要素，也是贪心算法与动态规划算法的主要区别。
贪心算法通常以自顶向下的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题，然后再求解一次贪心选择后产生的子问题解。
一个具体问题，要确定它是否具有贪心选择性质，须证明每一步所作的贪心选择最终导致问题的整体最优解。

3、贪心算法求解步骤

按照贪心选择策略对数据进行预处理（排序）；
从问题初始状态开始；
采用循环语句，当可以向求解目标前进一步时，就根据局部最优策略，贪心地得到一个部分解，并缩小问题范围或规模；
将所有部分解综合起来，得到问题的最终解。

4、贪心算法和动态规划算法的异同点

共同点：贪心算法和动态规划算法都要求问题具有最优子结构性质

不同点：①动态规划通常以递推方式求解各个子问题，某个问题的解依赖于已知子问题的解再做出选择。

②贪心算法依赖于一系列的局部贪心选择和求解每个局部阶段先做贪心选择再解子问题。

5、贪心算法实例

①活动安排问题

设有n个活动的集合，其中每个活动都要求使用同一资源（如演讲会场等），而在同一时间内只有一个活动能使用这一资源。
每个活动i都有要求使用该资源的起始时间si和结束时间fi，且。如果选择了活动i，则它在半开时间区间[si, fi)内占用资源。
若区间[si, fi)与区间[sj, fj)不相交，则称活动i与活动j是相容的。也就是说，当或时，活动i与活动j相容。

如何安排n个活动，令最多的活动使用资源？即如何高效地安排最多的活动使用某一公共资源？

【例】11个活动的开始时间和结束时间按结束时间的非减序排列如下：

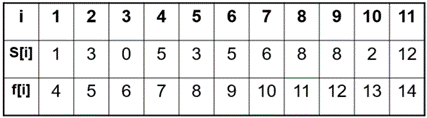
求活动安排。

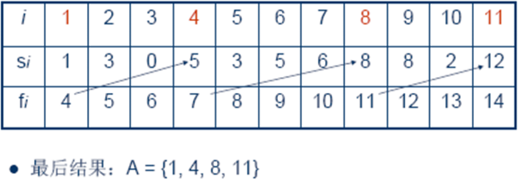
②背包问题

与0-1背包问题相似，不同的是，在选择物品i装入背包时，可以选择物品i的一部分，而不一定全部装入背包，。

这两类问题都具有最优子结构性质，极为相似，但背包问题可用贪心算法求解得到最优解，0-1背包问题却不能用贪心算法求解。

6、哈夫曼编码

字符的二进制编码方式：

固定长编码：每个字符都用相同长度的0, 1串表示。
可变长编码：经常出现的字符用短码，不常出现的用长码。

哈夫曼编码：数据文件压缩的编码方法。其压缩率通常在20%~90%之间。

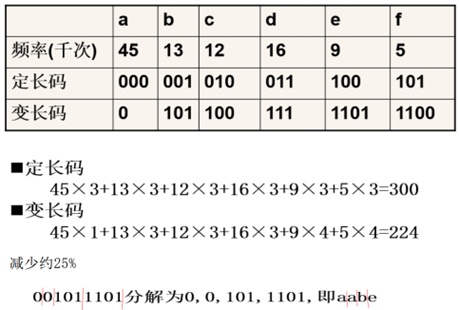
依据字符在文件中出现的频率，来建立用0/1串表示字符集的最优表示方式。
出现频率高的字符用较短编码，出现频率较低的字符用较长编码，以缩短文件总码长。

【例】

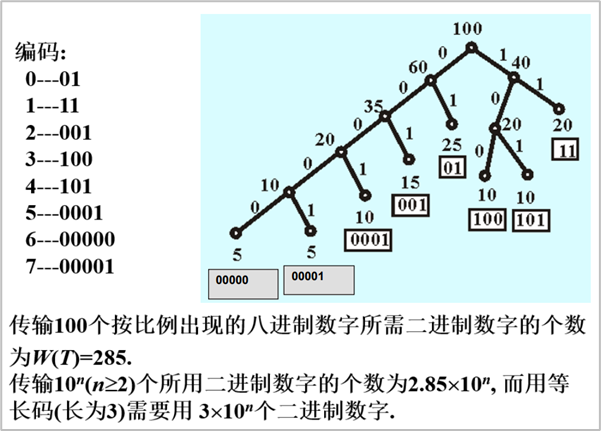
解：求以频率为权值的哈夫曼树，其中。构造的哈夫曼树如图所示。

7、单源最短路径

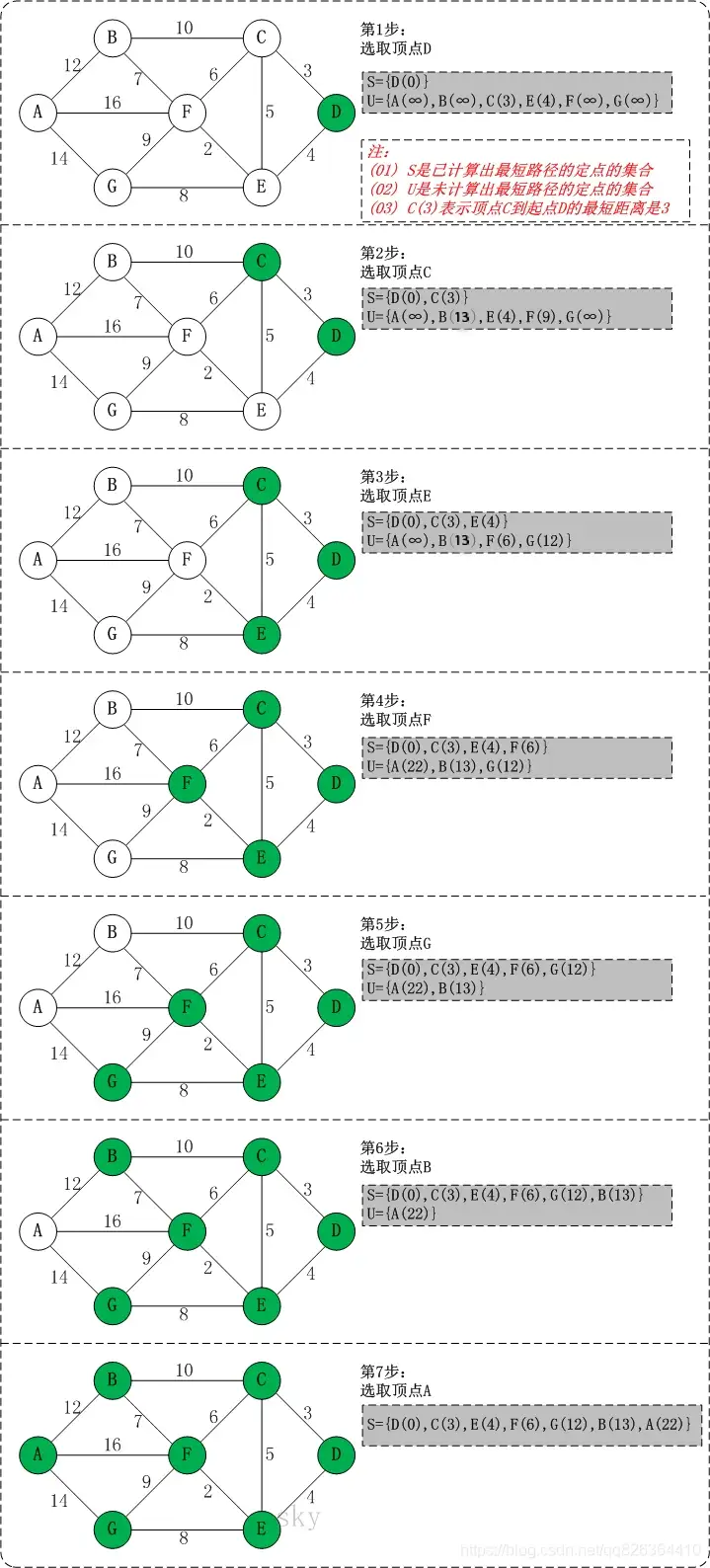
Dijkstra算法

8、最小生成树

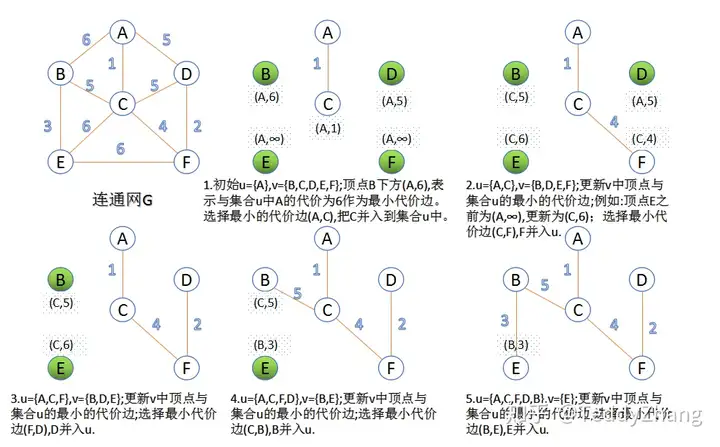
①Prime算法

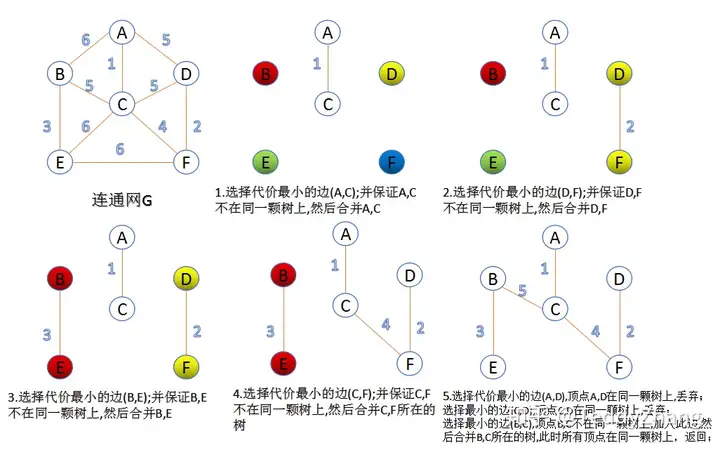
②Kruskal算法

二、算法实验1：完成教材114页算法实现题4-2，总结实验出现问题及解决方法。

最优合并问题：给定k个排好序的序列，用2路合并算法将这k个序列合并成一个序列。假设采用的2路合并算法合并2个长度分别为m和n的序列需要m+n-1次比较。试设计一个算法确定合并这个序列的最优合并顺序，使所需的总比较次数最少。为了进行比较，还需要确定合并这个序列的最差合并顺序，使所需的总比较次数最多。

#include<bits/stdc++.h>
using namespace std;
 
bool cmp(int a,int b) {
	return a>b;
}
 
int MaxMerge(int a[],int k) {
	int max=0;
	for(int i=0; i<k-1; i++) {
		sort(a+i,a+k,cmp);
		a[i+1]=a[i]+a[i+1];
		max=max+a[i+1]-1;
	}
	return max;
}
 
int MinMerge(int b[],int k) {
	int min=0;
	for(int i=0; i<k-1; i++) {
		sort(b+i,b+k);//升序排列
		b[i+1]=b[i]+b[i+1];
		min=min+b[i+1]-1;
	}
	return min;
}
 
int main() {
	int k;
	cin>>k;
	int a[k],b[k];
	int x;
	for(int i=0; i<k; i++) {
		cin>>x;
		a[i]=x;
		b[i]=x;
	}
	cout<<MaxMerge(a,k)<<" "<<MinMerge(b,k)<<endl;
	return 0;
}

时间复杂度：

最少比较次数：O（nlogn)

最多比较次数：O（n）

空间复杂度：O（n）

三、算法实验2：完成教材118页算法实现题4-14，总结实验出现问题及解决方法。

多元Huffman编码问题：在一个操场的四周摆放着n堆石子。现要将石子有次序地合并成一堆。规定每次至少选2堆，最多选k堆石子合并成新的一堆，合并的费用为新的一堆的石子数。试设计一个算法，计算出将n堆石子合并成一堆的最大总费用和最小总费用。

#include <iostream>
#include <queue>///队列库函数
using namespace std;
long long int max_sum;
long long int min_sum;

priority_queue <int, vector<int>, less<int> > q1;
priority_queue <int, vector<int>, greater<int> > q2;
void get_maxsum();
void get_minsum(int);
int main()
{
    int n, k, x;
    cin >> n >> k;
    for(int i = 0; i < n; i++)
    {
        cin >> x;
        q1.push(x);
        q2.push(x);
    }
    max_sum = min_sum = 0;
    get_maxsum();
//    cout << "----------" << endl;
    get_minsum(k);
//    cout << "----------" << endl;
    cout << max_sum << " " << min_sum << endl;
    return 0;
}
void get_maxsum()
{
    long long sum = 0;
//    cout << "q1.size = " << q1.size() << endl;
    while((int)q1.size() >= 2)
    {
        sum = 0;
        for(int i = 0; i < 2; i++)
        {
            sum += q1.top();
            q1.pop();
        }
        q1.push(sum);
        max_sum += sum;
//        cout << "q1.size = " << q1.size() << endl;
    }
}
void get_minsum(int k)
{
    long long sum = 0;
    while(q2.size() % (k-1) != 1)
    {
        q2.push(0);
    }
//    cout << "q2.size = " << q2.size() << endl;
    while((int)q2.size() >= k)
    {
        sum = 0;
        for(int i = 0; i < k; i++)
        {
            sum += q2.top();
            q2.pop();
        }
        q2.push(sum);
        min_sum += sum;
//        cout << "q2.size = " << q2.size() << endl;
    }
}