144
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享“贪心”顾名思义,因此其规律特征就是更加注重当前的状态,贪心法做出的选择是对于当前所处状态的最优选择,它的解决问题的视角是微观的“局部”,而不是从全局宏观的角度思考和看待问题。也就是说,不从整体最优上加以考虑,仅是某种意义上的局部最优解 。贪心算法通过一系列的选择得到问题的解,所做的选择都是当前状态下局部最好选择,这就是贪心选择。
1、贪心选择性质:一个问题的整体最优解可通过一系列局部的最优解的选择达到,并且每次的选择可以依赖以前作出的选择,但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解
2、最优子结构:当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中,至于什么问题具有什么样的贪心选择性质是不确定的,需要具体问题具体分析 。
1、将问题分解为若干个子问题
2、找出适合的贪心策略
3、求解每一个子问题的最优解
4、将局部最优解堆叠成全局最优解
贪心算法是比较抽象的,我们在解决算法题的时候不一定能从题目中直接看出是使用的贪心算法,这就需要我们一步一步的推导,同时贪心算法也是经典的算法,应用于许多生活场景中,虽然不一定是全局最优解但是局部最优解已经是很难得了,因此必须熟练掌握这一算法。
贪心算法:对于 0-1 背包问题,贪心选择不能得到最优解。贪心算法是计算每一件物品的单位价值然后每次选取最大价值的物品,在这种情况下,算法无法保证最终能将背包装满,部分闲置背包空间使每公斤背包空间的价值降低。
动态规划算法:在考虑 0-1 背包问题时,比较了选择该物品和不选择该物品的所有可能方案,最后在所有方案中找出最好选择。并导出许多互相重叠的子问题。
两种算法的异同:
1、贪心算法和动态规划算法都要求问题具有最优子结构性质,这是两类算法的共同点。
2、动态规划法通常以递推方式求解各个子问题,某个子问题的解依赖于已知子问题的最优解再作出选择。
3、贪心算法通常以一系列的局部贪心选择和求解,每个局部阶段,先作贪心选择,再解子问题。
贪心算法能够做到局部最优解,在本题中:`
(1)如果你想要的是最多比较次数的合并方案,那么就要每一次合并的时候都是该序列中最长的那两个。
(2)如果你想要的是最少比较次数的合并方案,那么就要每一次合并的时候都是该序列中最短的那两个。
所采用的2 路合并算法合并2 个长度分别为m和n的序列需要m + n -1次比较(题目已给出),把这个序列合并在一起之后在接着计算,即可得出最优值。所以,一定要先对序列进行排序。
def Most(num):
num1=num.copy()
#将列表num1降序排列
num1.sort(reverse=True)
print(num1)
Times=0#总的比较次数
times=0#每两个序列的比较次数
for i in range(n-2):
#取序列长度最长的两个序列先进行比较
times=num1[0]+num1[1]
Times=Times+times-1
#删除已比较的序列
del num1[0]
del num1[0]
#加入合并后的序列
num1.append(times)
num1.sort(reverse=True)
times=num1[0]+num1[1]-1
Times=Times+times
return Times
def Least(num):
num2=num.copy()
#将列表num2升序排列
num2.sort()
print(num2)
Times=0#总的比较次数
times=0#每两个序列的比较次数
for i in range(n-2):
#取序列长度最短的两个序列先进行比较
times=num2[0]+num2[1]
Times=Times+times-1
#删除已比较的序列
del num2[0]
del num2[0]
#加入合并后的序列
num2.append(times)
num2.sort()
times=num2[0]+num2[1]-1
Times=Times+times
return Times
#从文件中读出数据
file_readpath = 'data/1.txt'
with open(file_readpath) as file:
txt = file.read()
txt=txt.split('\n')
#n代表数据的个数
n=eval(txt[0])
num=[]
txt=txt[1].split()
for i in range(n):
num.append(eval(txt[i]))
most=Most(num)
least=Least(num)
print("最多次数为:",most)
print("最少次数为:",least)
#将结果存入文件output.txt
file_writepath = 'data/output.txt'
file=open(file_writepath,"w")
file.write(str(most)+' '+str(least))
file.close()
输入文件:
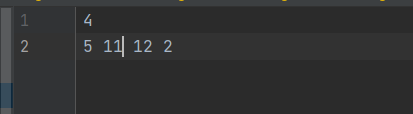
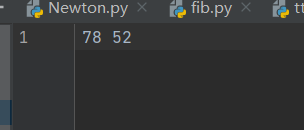
#从文件中读出数据
file_readpath = 'data/1.txt'
with open(file_readpath) as file:
txt = file.read()
txt=txt.split('\n')
#n代表n堆石子,k表示最多选k堆石子合并
txt1=txt[0].split()
n = eval(txt1[0])
k = eval(txt1[1])
arr=[]
txt=txt[1].split()
for i in range(n):
arr.append(eval(txt[i]))
arr.sort()
max = 0
temp_1 = arr[n - 1]
for i in range(n - 2, -1, -1):
if arr[i] == 0:
break
temp_1 += arr[i]
max += temp_1
i = 0
min = 0
temp_2 = 0
while i < n - 1:
temp_2 = 0;
arr = arr + [0]
for j in range(0, k):
temp_2 += arr[i]
i += 1
arr[n] = temp_2
n += 1
min += temp_2
arr[i:n] = sorted(arr[i:n])
print("最大总费用为:", max)
print("最小总费用为:", min)
file_writepath = 'data/output.txt'
file=open(file_writepath,"w")
file.write(str(max)+' '+str(min))
file.close()
输入文件:
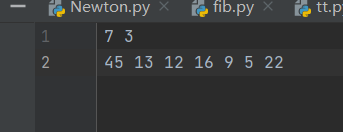
输出文件: