计硕三班 2022222319 冯绍杰第四章作业

Shojaei 2022-12-31 12:41:12

1. 概括第四章学习内容，总结第四章学习心得。

贪心算法又称贪婪算法，常常用于优化问题近似解的求解，求解过程中从问题的初始状态出发，通过若干次贪心选择而得出问题最优解。其有最优子结构性质和贪心选择性质，最优子结构性质是一个问题的最优解包含其子问题的最优解时，称此问题满足最优性原理。贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择得到。

贪心算法的求解步骤：

按照贪心选择策略对数据进行预处理；
从问题初始状态开始；
采用循环语句，向求解目标前进一步，根据局部最优策略，贪心的得到一个部分解，缩小问题范围或规模；
将所有部分解综合起来，得到问题的最终解。

应用实例：

活动安排问题、Huffman编码、单源最短路径

学习心得：

通过本章的学习，我深刻的理解了贪心算法的一些相关原理与思想，也从背包问题中体会到动态规划算法与贪心算法之间的一些异同点。贪心算法适用于无后效性的问题。因为一般贪心算法的思路就是建立问题的数学模型，然后将问题进行拆分，去求子问题的最优解，最后将子问题的最优解合成问题的解。贪心算法的优点在于做决策只要考虑当前情况，条件较为简单，问题的复杂度大大降低。但其缺点就是局部的最优解不一定是全局的最优解。通过学习这些内容使我明白不同的算法用在不同的实例上具有不同的作用，应将学习到的算法合理的用在各个实例之中，以便于更好的解决问题。

2. 以{0-1}背包问题和背包问题为例，讨论动态规划算法与贪心算法的异同。

贪心算法和动态规划都要求问题具有最优子结构性质，不同的是，动态规划算法只有在解决相关子问题后才能做出相应选择，因而只有在解出相关子问题时才能做出选择。贪心算法在当前状态下做出最好选择，然后继续求解做出该选择后产生的子问题。动态规划自底向上解子问题，贪心算法自顶向下解子问题。

以0-1背包和背包问题为例：

（1）0-1背包问题，物品不可分割。这时候使用贪心算法，很有可能导致浪费大量背包空间，局部的最优解往往不等于全局最优解。这类问题需要使用动态规划求解。

（2）背包问题，物品可以分割。这类问题就可以使用贪心算法，由局部最优解得到全局最优解。

总结：对于无后效性，有最优局部解的问题，使用贪心算法能够大大的降低问题复杂度，解决起来非常方便快捷。

3. 算法实验2：完成教材114页算法实现题4-2，总结实验出现问题及解决方法。

n = int(input())
a = list(map(int, input().split(',')))
w1=int(0)
w2=int(0)
i=int(0)
sm=sorted(a)#从小到大排序
big=sorted(a,reverse=True)#从大到小排序
while(i<n-1):
    w1=w1+sm[i]+sm[i+1]-1#2个长度分别为m和n的序列需要m+n -1次比较
    sm[i]=sm[i]+sm[i+1]
    sm[i+1]=0
    w2 = w2 + big[0] + big[1] - 1  # 2个长度分别为m和n的序列需要m+n -1次比较
    big[1] = big[0] + big[1]
    big[0] = 0
    i+=1
    sm.sort()
    big = sorted(big, reverse=True)  # 从大到小排序
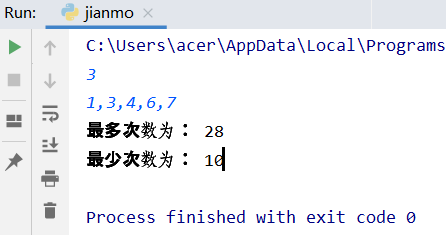
print("最多次数为：",w2)
print("最少次数为：",w1)

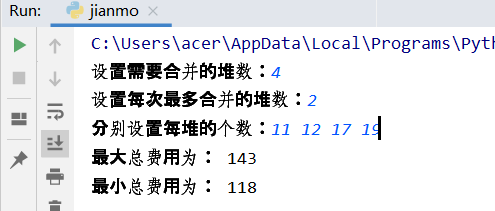
4. 算法实验2：完成教材118页算法实现题4-14，总结实验出现问题及解决方法。


n = int(input("设置需要合并的堆数："))
k = int(input("设置每次最多合并的堆数："))
arr = input("分别设置每堆的个数：")
p = [int(i) for i in arr.split()]
p.sort()
# 最大总费用
max = 0
max_spend = p[n - 1]
for i in range(n - 2, -1, -1):
    if p[i] == 0:
        break
    max_spend += p[i]
    max += max_spend
# 最小总费用
i = 0
min = 0
min_spend = 0
while i < n - 1:
    min_spend = 0
    p = p + [0]
    for j in range(0, k):
        min_spend += p[i]
        i += 1
    p[n] = min_spend
    n += 1
    min += min_spend
    # 将i-n部分排序
    p[i:n] = sorted(p[i:n])
print("最大总费用为：", max, "\n最小总费用为：", min)