计硕三班-杨阳-2022222300 第四章

[yangyang0428]

1. 概括第四章学习内容，总结第四章学习心得

贪心算法概念

贪心算法（greedy algorithm  ，又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。

贪心算法思想

贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。当然，希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。如单源最短路经问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似。
 

贪心算法基本要素

1.贪心选择性质。所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。

动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常以自顶向下的方式进行，以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题。

对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。

2. 当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。

贪心算法基本思路

从问题的某一个初始解出发逐步逼近给定的目标，以尽可能快的地求得更好的解。当达到算法中的某一步不能再继续前进时，算法停止。

该算法存在问题：

1. 不能保证求得的最后解是最佳的；

2. 不能用来求最大或最小解问题；

3. 只能求满足某些约束条件的可行解的范围。

2. 以{0-1}背包问题和背包问题为例，讨论动态规划算法与贪心算法的异同

对于0-1背包问题，贪心选择不能得到最优解。 因为在这种情况下，算法无法保证最终能将背包 装满，部分闲置背包空间使每公斤背包空间的价值降低。

动态规划算法在考虑0-1背包问题时，比较了选 择该物品和不选择该物品的所有可能方案，最后 在所有方案中找出最好选择。并导出许多互相重叠的子问题。这正是该问题用动态规划算法求解 的一个重要特征。

3. 算法实验2：完成教材114页算法实现题4-2，总结实验出现问题及解决方法

最优合并问题：给定k个排好序的序列，用2路合并算法将这k个序列合并成一个序列。假设采用的2路合并算法合并2个长度分别为m和n的序列需要m+n-1次比较。试设计一个算法确定合并这个序列的最优合并顺序，使所需的总比较次数最少。为了进行比较，还需要确定合并这个序列的最差合并顺序，使所需的总比较次数最多。

代码运行：

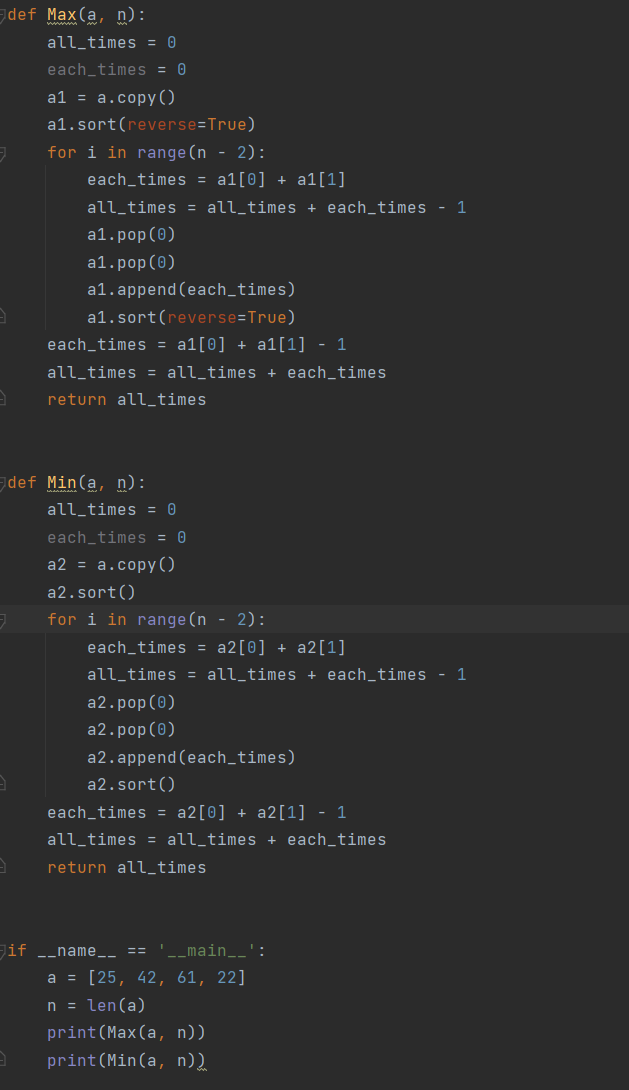
运行结果：

4. 算法实验2：完成教材118页算法实现题4-14，总结实验出现问题及解决方法 

多元Huffman编码问题：在一个操场的四周摆放着n堆石子。现要将石子有次序地合并成一堆。规定每次至少选2堆，最多选k堆石子合并成新的一堆，合并的费用为新的一堆的石子数。试设计一个算法，计算出将n堆石子合并成一堆的最大总费用和最小总费用。

运行代码：