计硕三班-郭思阳-2022222260-第四章

[kccol]

一、概括第四章学习内容，总结第四章学习心得

1.贪心算法

贪心算法，又称贪婪算法，是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。

2.基本性质

（1）贪心选择性质：指所求问题的整体最优解可以通过一系列局部最优的选择（贪心选择）得到。 这是贪心算法可行的第二个基本要素，也是贪心算法与动态规划算法的主要区别。

（2）最优子结构性质：一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质，也称此问题满足最优性原理。

3.相关问题

（1）哈夫曼编码问题

（2）单源点最短路径问题

（3）最小生成树问题

4.学习心得

通过这章对贪心算法的学习，对于贪心算法的理解更进一步。同时，对哈夫曼编码问题以及最短路径和最小生成树的手动的复现，对这几个问题也有了更深的理解。与动态规划不同的是，贪心算法在求解问题时，总是选择对于当前子问题最好的选择。要理解这两个算法的不同以及内在联系。

二、以“0-1背包”和"背包"问题为例，探讨动态规划算法与贪心算法异同

共同点：两者的共同点是都有最优子结构

不同点：于0-1背包问题，贪心选择不能得到最优解。因为在0-1背包问题中，物品只有放入和不放入两种情况，无法保证最终能将背包装满，部分闲置的背包空间使背包空间的价值降低。对于背包问题，物品可以部分放入背包中，这使得相同背包空间的价值更高。

动态规划算法在考虑0-1背包问题时，比较了选择该物品和不选择该物品的所有可能方案，最后在所有方案中找出最好选择。并导出许多互相重叠的子问题。这正是该问题用动态规划算法求解的一个重要特征。

三、算法实验2：完成教材114页算法实现题4-2，总结实验出现问题及解决方法。

1.最优合并问题

def Max(num):
    num1=num.copy()
    num1.sort(reverse=True)
    print(num1)
    Times=0
    times=0
    for i in range(n-2):
        times=num1[0]+num1[1]
        Times=Times+times-1
        del num1[0]
        del num1[0]
        num1.append(times)
        num1.sort(reverse=True)
    times=num1[0]+num1[1]-1
    Times=Times+times
    return Times
def Min(num):
    num2=num.copy()
    num2.sort()
    print(num2)
    Times=0
    times=0
    for i in range(n-2):
        times=num2[0]+num2[1]
        Times=Times+times-1
        del num2[0]
        del num2[0]
        num2.append(times)
        num2.sort()
    times=num2[0]+num2[1]-1
    Times=Times+times
    return Times

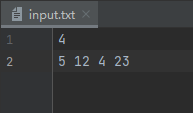
file_readpath = 'input.txt'
with open(file_readpath) as file:
    txt = file.read()
txt=txt.split('\n')
n=eval(txt[0])
num=[]
txt=txt[1].split()
for i in range(n):
    num.append(eval(txt[i]))
 
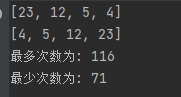
max=Max(num)
#print(duo)
min=Min(num)
#print(Shao)
print("最多次数为:"max)
print("最少次数为:"min)
 
file_writepath = 'output.txt'
file=open(file_writepath,"w")
file.write(str(max)+' '+str(min))
file.close()
 

 

 

2.多元哈夫曼编码问题

 

 

 

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n;
int dp_max[207][207];
int dp_min[207][207];
int cost[207];
int a[203];
const int MAX = 0x3f3f3f3f;
 
int main()
{
	while (scanf("%d", &n) != EOF)
	{
		memset(dp_min, MAX, sizeof(dp_min));
		memset(dp_max, 0, sizeof(dp_max));
		for (int i = 1; i <= n; i++)
		{
			scanf("%d", &a[i]);
			a[i + n] = a[i];
			dp_min[i][i] = 0;
			dp_min[i + n][i + n] = 0;
		}
		cost[0] = 0;
 
		for (int i = 1; i <= 2 * n; i++)//为了后面方便用前缀和
			cost[i] = cost[i - 1] + a[i];
 
		for (int len = 2; len <= n; len++)//走几步 
		{
			for (int i = 1; len + i - 1 <= 2 * n; i++)//从哪开始 
			{
				int j = len + i - 1;
				for (int k = i; k < j; k++)
				{
					dp_min[i][j] = min(dp_min[i][j], dp_min[i][k] + dp_min[k + 1][j] + cost[j] - cost[i - 1]);
					dp_max[i][j] = max(dp_max[i][j], dp_max[i][k] + dp_max[k + 1][j] + cost[j] - cost[i - 1]);
				}
			}
		}
		int ans_min = MAX;
		int ans_max = -1;
		for (int i = 1; i <= n; i++)
		{
			ans_min = min(ans_min, dp_min[i][i + n - 1]);
			ans_max = max(ans_max, dp_max[i][i + n - 1]);
		}
		cout << ans_min << " " << ans_max << endl;
	}
	return 0;
}