计硕2班 金王煜 2022222237 《贪心策略》

[淼淼大帅比]

1. 学习内容概括及学习心得

1.1 学习内容概括

1.2 学习心得

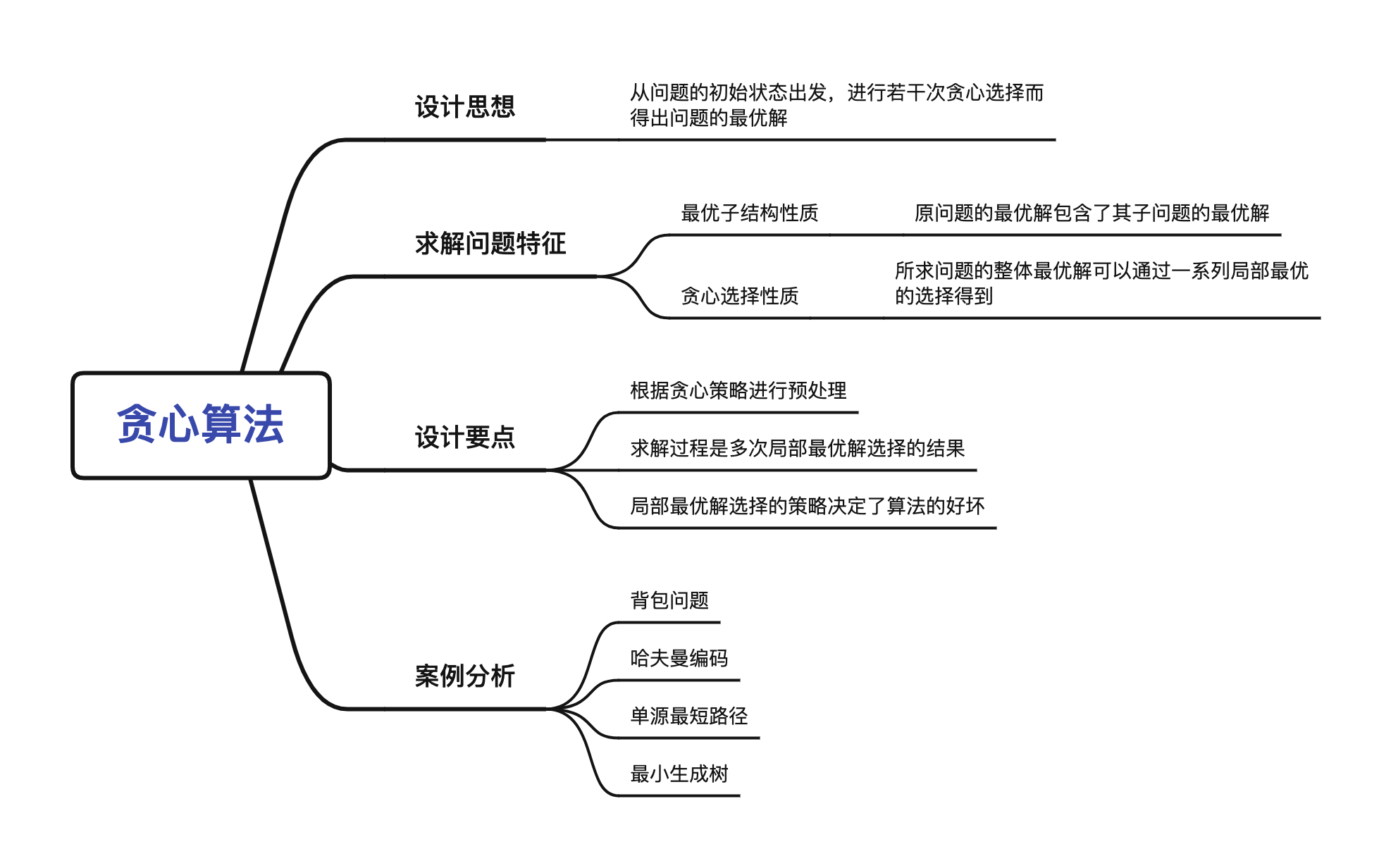
本章系统的学习了贪心算法的算法思想、设计特点以及可解决问题的特征，通过案例分析，让我在解决问题的过程中实际体验到了贪心算法设计特点中所提到的内容。虽然贪心算法的框架是固定的，但是在针对不同具体问题的过程中，各个框架部分的具体处理方法又会有所不同，比如针对数据的预处理策略可能不同，每一步贪心选择的判断依据也可能不相同。所以，贪心策略也是十分灵活的，针对不同问题的具体应用步骤也是各有千秋。

2. 算法设计与分析

2.1 以{0-1}背包问题和背包问题为例，讨论动态规划算法与贪心算法的异同。

• 不同点：

贪心算法对于0-1背包问题来说，可能无法得到最优解，因为算法无法保证最终可以装满，部分闲置背包空间可能使每公斤背包的价值降低；而使用动态规划算法时，算法比较了选择和不选择物品的所有可能方案，并导出重叠子问题，而这恰恰是使用动态规划问题的特征。

• 相同点：

两者都依赖于局部最优的子结果来得到原问题的全局最优结果

2.2 算法实验1：完成教材114页算法实现题4-2，总结实验出现问题及解决方法。

2.2.1 问题描述

给定k个排好序的序列，用2路合并算法将这k个序列合并成一个序列。假设采用的2路合并算法合并2个长度分别为m和n的序列需要m+n-1次比较。试设计一个算法确定合并这个序列的最优合并顺序，使所需的总比较次数最小。为了进行比较，还需要确定合并这个序列的最差合并顺序，使所需的总比较次数最少。

2.2.2 问题分析与求解

• 问题分析

  对于给定的k个待合并序列，计算最多比较次数和最少比较次数合并方案。

• 问题求解

  import java.util.Scanner;
  public class exp3 {
      public static void bubbleSort(int[] arr, int start, int end) {
          // 从小到大排序
          for (int i = start; i < end-1; i++)
              for (int j = 0; j < end - 1 - i; j++)
                  if (arr[j] > arr[j + 1]) {
                      int temp;
                      temp = arr[j];
                      arr[j] = arr[j + 1];
                      arr[j + 1] = temp;
                  }
      }
  
      static int minsum(int a[], int m) {
          int n =m;
          int[] b = new int[n];
          int sum = 0;
          for (int i = 0; i < n; i++) {
              b[i] = a[i];
          }
          while (m > 1) {
              bubbleSort(b, 0, m);
              b[0] = b[0] + b[1];
              sum += b[0];
              for (int i = 1; i < m - 1; i++) {
                  b[i] = b[i + 1];
              }
              m--;
          }
          return sum ;
      }
  
      static int maxsum(int a[], int m) {
          int n = m;
          int s=0;
          int[] b = new int[n];
          int sum = 0;
          for (int i = 0; i < n; i++) {
              b[i] = a[i];
          }
          while (s < m - 1) {
              bubbleSort(b, s, m);
              b[m - 1] = b[m - 2] + b[m - 1];
              sum += b[m - 1];
              for (int i = m-2; i >s; i--) {
                  b[i] = b[i -1];
              }
              s++;
          }
          return sum;
      }
      public static void main(String[] args) {
          {
              Scanner sc = new Scanner(System.in);
              int[] a = new int[100];
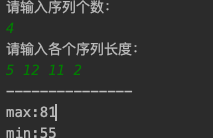
              System.out.println("请输入序列个数：");
              int num = sc.nextInt();
              System.out.println("请输入各个序列长度：");
              for (int i = 0; i < num; i++)
                  a[i] = sc.nextInt();
              System.out.println("---------------");
              System.out.println("max:"+maxsum(a, num));
              System.out.println("min:"+minsum(a, num));
          }
      }
  }
  

• 实验结果

2.3 算法实验2：完成教材118页算法实现题4-14，总结实验出现问题及解决方法。

2.3.1 问题分析与求解

• 问题求解

  import java.util.ArrayList;
  import java.util.Scanner;
  
  import static java.util.Arrays.sort;
  
  public class exp4 {
  
      public static void main(String[] args) {
          System.out.println("请输入总堆数n和每次要移动的堆数k：");
          Scanner sc = new Scanner(System.in);
          int n = sc.nextInt();
          int k = sc.nextInt();
          int[] pile= new int[n];
          System.out.println("请输入每堆的石子数：");
          for (int i = 0; i < n; i++) {
              pile[i] = sc.nextInt();
          }
          sort(pile);
          int max = maxfee(pile);
          int min = minfee(pile, k);
          System.out.println("---------------------");
          System.out.println("max:"+max);
          System.out.println("min:"+min);
      }
  
  
      private static int minfee(int[] pile, int k) {
          int min = 0;
          ArrayList<Integer> temp = new ArrayList<>();/
          for (int i = 0; i < pile.length; i++) {
              int add = 0;
              for (int j = 0; j < k; j++)
                  add += pile[i++];
  
          }
          if (add != pile[pile.length - 1])
              min += add;
          temp.add(add);
          i--;
      }
      int[] p = new int[temp.size()];
          for (int i = 0; i < p.length; i++) {
          p[i] = temp.get(i);
      }
          if (temp.size() != 1) {
          minfee(p, k);
      }
          return min;
  }
  
  
      private static int maxfee(int[] pile) {
          int max;
          ArrayList<Integer> temp = new ArrayList<>();
          for (int i = 0; i < pile.length; i++) {
              int add = 0;
              for (int j = k - 1; j > 0; j--)
                  add += pile[i++];
  
              if (add != pile[pile.length - 1])
                  max+= add;
              temp.add(add);
              i--;
          }
          int[] p = new int[temp.size()];
          for (int i = 0; i < p.length; i++) {
              p[i] = temp.get(i);
          }
          if (temp.size() != 1) {
              minfee(p, k);
          }
          return max;
      }
  }