递归-------斐波那契

[2007向凤盏]

思想：（将一个复杂的大问题拆分为小问题来解决)一个问题的解等价于拆分为子问题的解。子问题规模变小，但是子问题与原问题思路相同。
存在终止条件(符合算法的有限性)
优点：递归思想简单，容易理解思考；缺点：空间复杂度高，堆栈溢出分险，耗时比较高，重复计算问题。
 

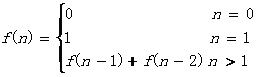
1.递归法解决问题，自顶向下计算，时间复杂度高。T(n)＝O(n2)

#递归fibonacci

def fun(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fun(n-1) + fun(n-2)

n = int(input())
num = fun(n)
print(num)

2.递归中存在重复计算问题，将已经计算过的值保存到字典。T(n)=O(n)

#hashmap()存储已经计算的值

di = {}
def func(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        if n in di:
            return di.get(n)
        else:
            result = func(n-1) + func(n-2)
            di[n] = result
            return result

n = int(input())
num = func(n)
print(num)

3.循环方式，自底向上累加，难理解(用变量临时保存子问题的解)。T(n)=O(n)
 

#循环，自底向上

def fibonacci(n):
    a = 0
    b = 1
    if n == 0:
        return 0
    elif n == 1:
        return 1
    for i in range(1,n):
        c = a+b
        a = b
        b = c
    return b

n = int(input())
num = fibonacci(n)
print(num)