蓝桥算法训练营—普及组 day01 (c++)

[5tayhumb1e]

1.P2694 接金币

---

模拟题
其实也被卡了一会，我是废物

1.c++代码

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;

const int N = 10000;

struct graph{
    int x,y;
}graphs[N];

int t;

bool cmp(graph a,graph b){
    return a.y <= b.y;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    cin >> t;
    while(t --){
        int n;
        cin >> n;
        for(int i = 1; i <= n; i ++){
            cin >> graphs[i].x >> graphs[i].y;
        }
        sort(graphs + 1,graphs + 1 + n,cmp);
        
        int x = 0;
        int y = 0;
        bool flag = true;
        for(int i = 1; i <= n; i ++){
            if(abs(x - graphs[i].x) <= graphs[i].y - y){
                x = graphs[i].x;
                y = graphs[i].y;
            }else{
                flag = false;
                break;
            }
        }
        if(flag){
            cout << "Abletocatch" << endl;
        }else{
            cout << "Notabletocatch" << endl;
        }
    }
    return 0;
}

---

2.P1372 又是毕业季I

---

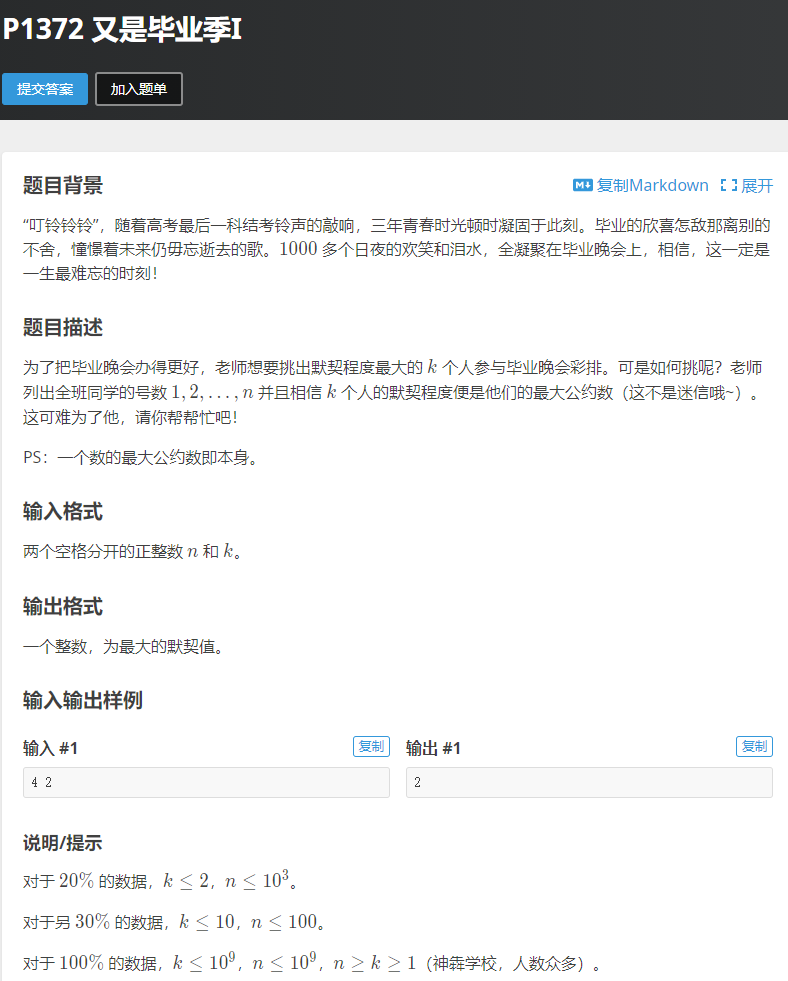
题目 意思就是：从1~n中取k个数，使这k个数的最大公约数最大
然后题目给了一个小提示：一个 整数的最大公约数 就是他本身

假设一个数是 x，x 和 2 * x 的最大公约数就是 x ， 设t 是一个未知数 ，且t * x <= n ，且 t * x 是最大的一个 x的倍数 且小于等于 n的存在
所以 x 和 2 * x 和 3 * x 和 4 * x .... t * x 的最大公约数就是 n
而很明显 如何使得 t * x 最大 且是从 k个数里面选择 ，那么就可以 看成 1* x ,2x ,3x , ... k * x 全都 <= n 即 t = k

这题其实我偷瞄了一下题解

1.c++代码

#include<iostream>

using namespace std;

int main(){
    int n,k;
    cin >> n >> k;
    cout << n / k;
    return 0;
}

---

3.P1106 删数问题

---

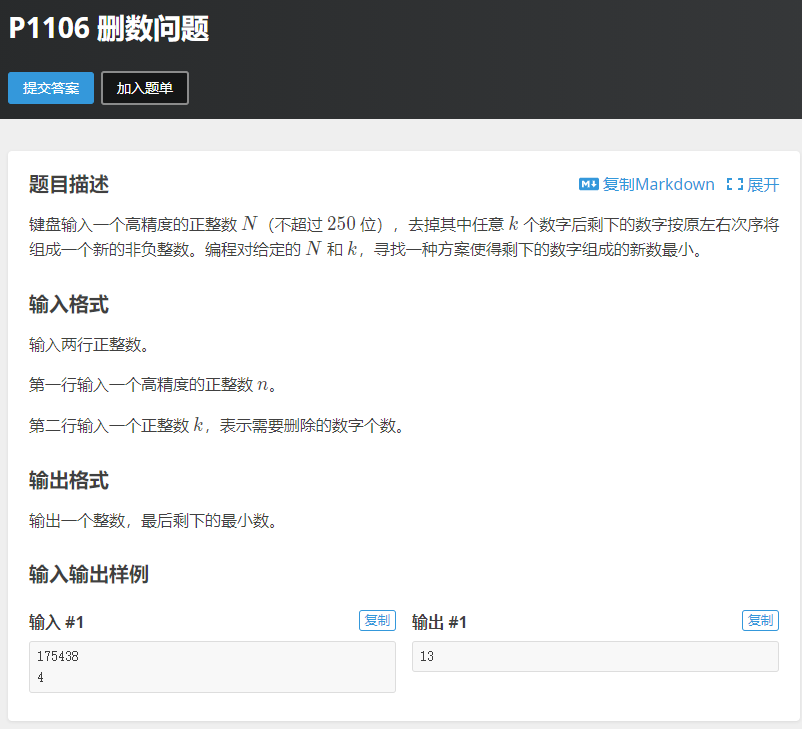
这题可以看成 一个 如何把高精度里的各个数放入一个 单调不递减的队列 的问题，但是要处理好 前导 0 的情况。属于是面向样例编程了这波

1.c++代码

#include<iostream>

using namespace std;

const int N = 1e3 + 10;
int q[N],hh = 0,tt = -1;

int main(){
    string a;
    int k;
    cin >> a >> k;
    for(int i = 0; i < (int)a.size(); i ++){

        if(k >= 0){
            while(hh <= tt && (a[i] - '0' < q[tt]) && k > 0){
                tt --;
                k --;
            }
            while(hh <= tt && q[tt] == 0 && k != 0){
                tt --;
            }
            q[++tt] = a[i] - '0';
        }
    }

    if(tt - k < 0){
        cout << 0;
        return 0;
    }else{
        bool flag = true;
        if(tt - k == 0){
            cout << q[0];
            return 0;
        }
        for(int i = 0; i <= tt - k; i ++){
            if(q[i] != 0 ){
                flag = false;
            }
            if(!flag){
                cout << q[i];
            }
        }
    }
    return 0;
}

---

4.谈判 - 蓝桥云课 (区间dp)

---

这题和 Acwing 148. 合并果子 是一模一样的

1.c++代码

#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;

int n;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    cin >> n;
    priority_queue<int,vector<int>,greater<int> > heap;
    for(int i = 0; i < n; i ++){
        int x;
        cin >> x;
        heap.push(x);
    }

    int res = 0;
    while(heap.size() > 1){
        int a = heap.top();
        heap.pop();
        
        int b = heap.top();
        heap.pop();
        res += a + b;
        heap.push(a + b);
    }
    
    cout << res;
    return 0;
}