【C++】2023.2.7打卡第六天_16（DFS+剪枝）

[三百题蓝桥省一战神]

剪格子

 

 

题目描述

如下图所示，3 x 3 的格子中填写了一些整数。

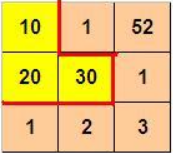
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 60。

本题的要求就是请你编程判定：对给定的 m×n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 0。

输入描述

输入描述

程序先读入两个整数m,n 用空格分割 (m,n<10)，表示表格的宽度和高度。

接下来是 n 行，每行 m 个正整数，用空格分开。每个整数不大于 104。

输出描述

在所有解中，包含左上角的分割区可能包含的最小的格子数目。

输入输出样例

示例

输入

3 3
10 1 52
20 30 1
1 2 3

 

输出

3

 我的解答

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

int X[]={-1,1,0,0};
int Y[]={0,0,-1,1};  //移动坐标需要的偏移量
int mp[10][10];  // 初始数组 
int ans[1000];  //存答案的数组 
bool use[10][10];   //格子选中状态 
int n,m,cnt;
long long sum;

void dfs(int x,int y,long long int num,int step)
{
	//递归出口 
	if(num==sum/2) 
	{
		ans[cnt++]=step;
		return ;
	}
	
	 //剪枝
	 if(x<0||x>n-1||y<0||y>m-1) return ;
	 if(num>sum/2)  return ;

	 //递归条件
	 for(int i=0;i<4;i++)   //递归分支
	 {
	 	//分支过后进入下一层
		x+=X[i];y+=Y[i];
		if(use[x][y]==false)
		{
			use[x][y]=true;
			dfs(x,y,num+mp[x][y],step+1);
			use[x][y]=false;  //回溯
		}
		x-=X[i];y-=Y[i];  //回溯
	 }
	  
}
int main()
{
	cin>>m>>n;  //先输入列，再输入行
	for(int i=0;i<n;i++)   //行
		for(int j=0;j<m;j++)  //列
		{
			cin>>mp[i][j];
			sum+=mp[i][j];
		}
	long long int num=mp[0][0];
	use[0][0]=true;
	dfs(0,0,num,1);
	sort(ans,ans+cnt);
	cout<<ans[0]<<endl;
	return 0;	
 } 

总结

1.做题时首先读清楚题意，读入、输入、输出。

本题就挖了一个坑：输入是：n 行每行 m 个正整数。但在第一行读入n和m时，是先读入的列m，再读入的行n。

解决方案：把列m放在行n前面先读入，交换读入顺序。

2.理清楚dfs参数和进入下一层dfs的条件来进行剪枝。

3.格子搜索题在蓝桥杯中比较常见，一定要闭着眼也能写出来。