蓝桥算法训练营—普及组 day03 (c++)

[5tayhumb1e]

1.P1049 [NOIP2001 普及组] 装箱问题(01背包)

---

这题就是01背包问题

1.c++代码

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 35, M = 2e4 + 10;

int f[N][M];//f[i][j]表示 已经装入第i个物品，且目前箱内已经装入体积还是 小于等于j 的时候的体积是多少
//f[i][j] <= j
//这题可以看成是一个01背包问题，体积就是每个物品的所占的体积，价值就是每个物品装后所填充的体积
//即f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + v[i]] 

int v[N];
int n,m;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> m >> n;

    for (int i = 1; i <= n; i++) {
        cin >> v[i];
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= m; j++) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) {
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + v[i]);
            }
        }
    }

    cout << m - f[n][m];//求的剩余空间，而f[n][m]表示装入n个物品后 所占的体积（所占体积 <= m)
    return 0;
}

---

2.P8647 [蓝桥杯 2017 省 AB] 分巧克力(二分)

---

1.c++代码

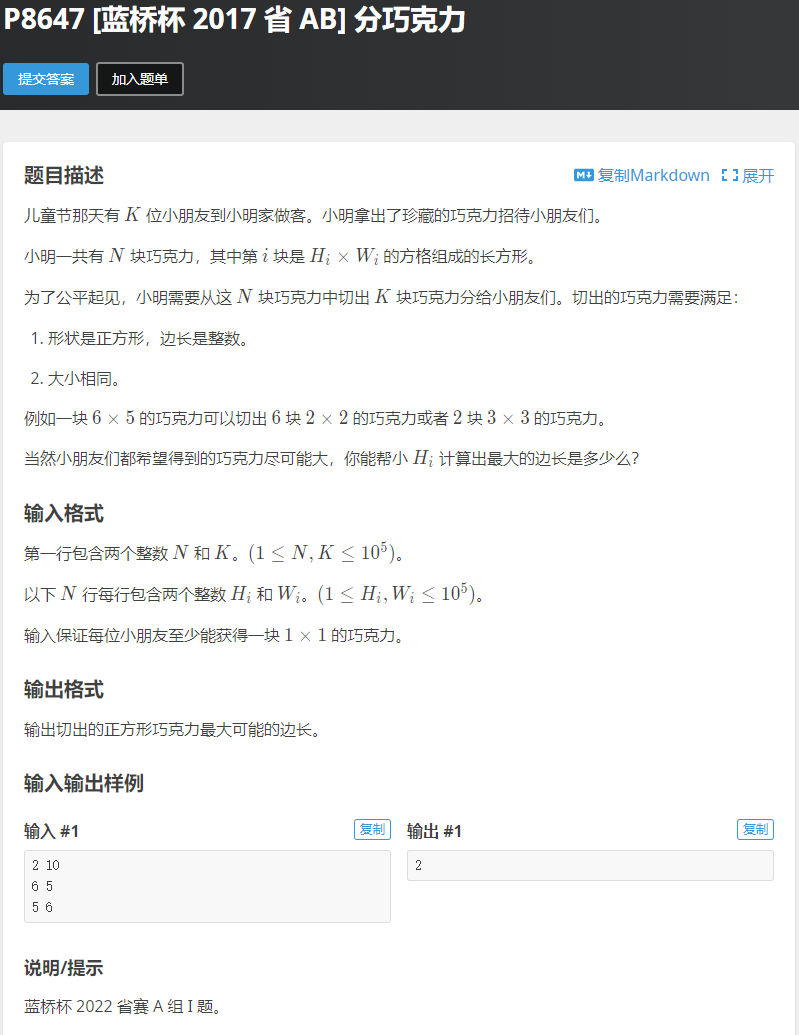
#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n,k;
int h[N],w[N];

bool check(int x){
    int sum = 0;
    
    for(int i = 1; i <= n; i ++){
        sum = sum + (h[i] / x) * (w[i] / x);
        if(sum >= k){
            return true;
        }
    }
    return false;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    cin >> n >> k;
    for(int i = 1; i <= n; i ++){
        cin >> h[i] >> w[i];
    }
    
    //这里是枚举的是 巧克力的最大边长
    //而二分性 则是巧克力的边长越大，能分出巧克力的块数越小
    //但是判断条件是 分出块数 必须是 大于等于 k
    int l = 0,r = 1e5 + 10; //h[] 和 w[]最大也才是1e5
    while(l < r){
        int mid = (l + r + 1) >> 1;
        if(check(mid)){
            l = mid;
        }else{
            r = mid - 1;
        }
    }

    //这里输出l 和 r都一样，
    //因为二分退出条件是 l != r ，而l是永远不会大于r的，所以l 只能等于 r
    cout << l; 
    return 0;
}

---

3.P1824 进击的奶牛(二分)

---

1.c++代码

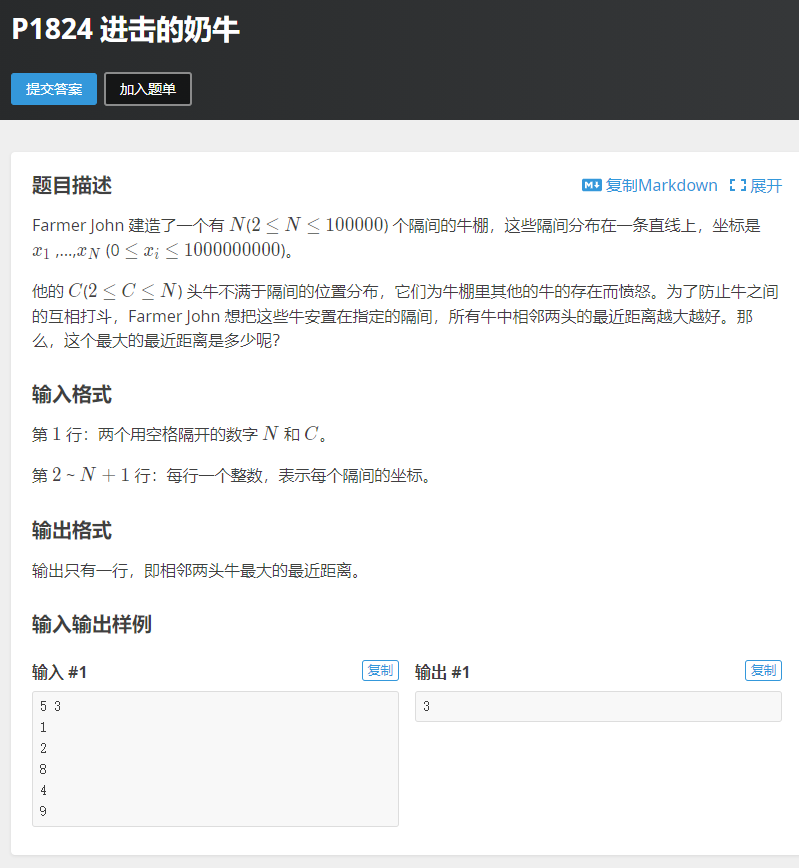
#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1e5 + 10;

int a[N];
int n, c;

bool check(int x) {
    int tmp = a[1];
    int cnt = 1; //最左边的牛 一定是被安排上的

    for (int i = 2; i <= n; i++) {
        if (a[i] - tmp >= x) {
            cnt++;
            tmp = a[i];
        }
        if (cnt >= c) {
            return true;
        }
    }
    return false;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> c;

    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a + 1, a + 1 + n);

    //二分枚举 距离，判断这个距离是不是最大的，且至少满足c头牛的情况下
    int l = a[1], r = a[n];
    while (l < r) {
        int mid = (l + r + 1) >> 1;
        if (check(mid)) {
            l = mid;
        }
        else {
            r = mid - 1;
        }
    }
    cout << l;
    return 0;
}

---

4.P1036 [NOIP2002 普及组] 选数(深度优先搜索)

---

1.c++代码

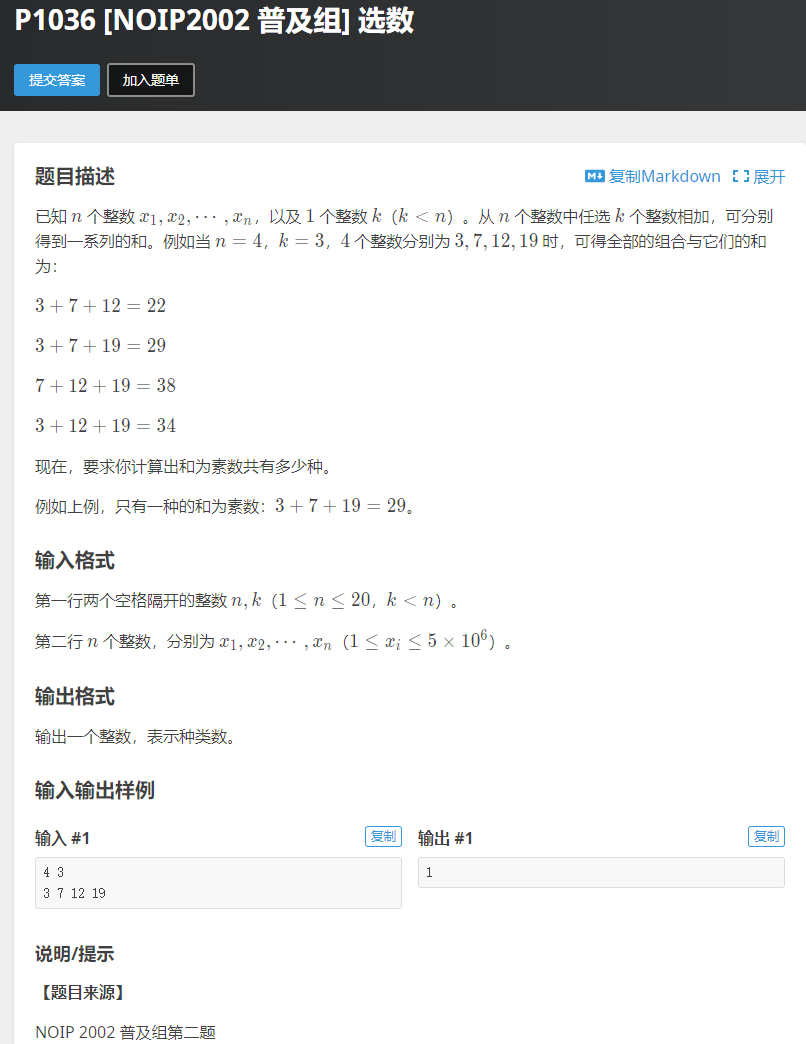
#include<iostream>
using namespace std;

const int N = 22;

int a[N];
bool st[N];//st[i] 表示a[i] 是否被用过,被用过则为true
int ans;
int n,k;

bool is_prime(int x){
    if(x < 2){
        return false;
    }
    for(int i = 2; i <= x / i; i ++){
        if(x % i == 0){
            return false;
        }
    }
    return true;
}

//u是代表a[]的下标 ，sum是表示选了多少个a[]的总和 ，cnt 表示是当前已经选取了多少个数
void dfs(int u,int sum,int cnt){
    if(cnt > k){
        if(is_prime(sum)){
            ans ++;
        }
        return;
    }
    
    for(int i = u; i <= n; i ++){
        if(st[i] == false){
            st[i] = true;
            dfs(i + 1,sum + a[i],cnt + 1);
            st[i] = false;
        }    
    }
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    cin >> n >> k;

    for(int i = 1; i <= n; i ++){
        cin >> a[i];
    }
    
    dfs(1,0,1); 
    
    cout << ans;
    return 0;
}

---