知乎热点算法问题？我竟在这本书里读到过答案！

[人邮异步社区]

数学的世界，看似繁复纷杂实则能简洁有序，看似枯燥无味实则能专业与趣味兼具，并深刻影响着众多学科的发展。

知乎上曾有一段话：“虽然说计算机和金融行业不能迷信数学，但这俩行业离开了数学，就是达内培训班和清华叉院的区别，就是银行柜员和文艺复兴的区别。”

 

异步君这两天刷知乎，看到了这么一个问题

立马就想起了前段时间所沉迷的吴军博士的新书《计算之魂》，书里刚好讲解了一道类似的题目。

有 12 个外观一模一样的球，其中 1 个球的质量和其他 11 个的不同，不妨称之为坏球，其他球称为好球。

坏球可能比好球轻一点，也可能重一点。现在给你一个天平，只能用天平称 3 次，如何找到那个坏球，并且确定它是轻一点还是重一点。

这道题不但其蕴含的数学原理精妙绝伦，吴军博士的讲解也非常具有启发性，甚至让我对于知乎上的这个问题立马就有了思路，忍不住拿起笔来写写画画，想要展示一下自己苦读《计算之魂》的成果~

购买链接：https://item.jd.com/13515688.html

 

第一步，读题

我们先思考N=12时的情况，再推广到N为一般值。要解决这个问题，必须读出题面下隐含的2个信息。

1．“称出来”，不是从12个球中称出1个特殊球，而是从24种情况中称出1种特殊情况。这24种情况分别是第1个球轻、第2个球轻、……、第12个球轻，以及第1个球重、第2个球重、……、第12个球重，我们最后要从这24种情况中确定一种。

2．用天平称重，结果不是“相同”或“不同”2种，而是左边轻、两边相同、左边重3种。类比二进制的比特（bit），我们可以将1次天平称重产生的可以区分3种状态的信息量称为1吹特（trit）。

 

第二步，解题

我们都知道，信息可以用来消除不确定性，不确定性越大，所需要的信息也就越多。

1吹特可以区分3种不同的信息，或者说完成3选1；类似地，2吹特可以区分32即9种不同的信息，3吹特可以区分33即27种。

现在有24种不同的情况要区分，因此3吹特是可以对它们进行编码区分的。

至此，将12个球推广到N个球。

 

N 个乒乓球中有一个和其他的质量不同，用天平最少几次一定能称出来？

 

设天平最少用k次能够称出重量不同的小球，可列方程3k≥2N>3k-1，解得k=[log32N]+1。

你以为到这里就结束了吗？

在《计算之魂》中，吴军博士立马就给出了另一个“打脸”的例题：

 

请证明如果是121个球，不可能用天平 5 次称出来。

 

异步君当时看到这个问题就懵了，当N=121时，k=[log32×121]+1≈[4.996]+1=5没错啊，为什么就不能用天平5次称出来呢？

对此，吴军博士给出了非常简洁的证明：

如果我们有121个球，假如第一次天平两边各放置N个，剩下的是121−2N个。

如果N≤40，剩下的球至少是41个，它有41×2=82种不确定的情况，无法通过4次称重消除不确定性，因为34=81。

如果N>40，它至少是41，如果称重的结果是一边高一边低，那么就有41（个轻的）+41（个重的）=82种不确定的情况，我们依然无法通过4次称重排除。

 

原来，前面的分析所考虑的天平称k次能提供3k个信息量，没有根据实际情况进行思考。

根据题目所说：

① N个乒乓球中有1个球和其他球的质量不同，那么这个球和其他球称重相等的情况就不可能出现；

② 这个特殊球的质量具体是偏轻还是偏重也是未知的，那么这个球比其他球重或比其他球轻的两种情况也不能当做得出最终结论的有效信息，因为无法据此判断出这个特殊球到底是偏轻的那个还是偏重的那个。

因此，在这个问题中，天平称k次只能提供(3k-3)个有效信息量，故解决此类问题所需列出的方程应为3k-3≥2N>3k-1-3。

解得k=[log3⁡2N+3]+1，为当N推广到一般情况的答案。

那么，要如何证明这个答案正确，也就是这个最少次数的称重方法要如何具体实现呢？

 

第三步，验证

还是以N=12为例，

有 12 个外观一模一样的球，其中 1 个球的质量和其他 11 个的不同，不妨称之为坏球，其他球称为好球。

坏球可能比好球轻一点，也可能重一点。现在给你一个天平，只能用天平称 3 次，如何找到那个坏球，并且确定它是轻一点还是重一点。

吴军博士在《计算之魂》中不仅给出了这道题的答案，还非常详细地梳理了解题思路和需要注意的“坑”。这里为大家简单梳理一下思路。

 

第一次称重：

将12个球分为3组，1～4号、5～8号和9～12号球各一组，将前2组放到天平左右两边称重，这样可以得到3种结果：

（1）左边轻，则说明1～4号球中有一个偏轻，或5～8号球中有一个偏重；

（2）平衡，则说明9～12号球中有一个偏轻，或9～12号球中有一个偏重；

（3）左边重，则说明1～4号球中有一个偏重，或5～8号球中有一个偏轻。

由于结果（1）和（3）对称，故后面只讨论情况（1）和情况（2）。

 

第二次称重：

对于情况（1）：

我们现在需要判断的可能情况有8种：1～4号球中有一个偏轻，或5～8号球中有一个偏重。另外，我们其实还获得了一个隐藏条件：9~12号球都是标准球。

所以，在这一步，我们可以将1、2、9号球放在天平左边，3、4、5号球放在天平右边，然后称重。此时，会出现3种情况：

（1.1）左边轻，说明可能的情况是1轻、2轻、5重，共3种可能；

（1.2）平衡，说明可能的情况是6重、7重、8重，共3种可能。

（1.3）左边重，说明可能的情况是3轻、4轻，共2种可能。

 

对于情况（2）：

需要判断的可能情况同样有8种：9～12号球中有一个偏轻，或9～12号球中有一个偏重。以及一个隐藏条件：1~8号球都是标准球。

所以，在这一步，我们可以把1～3号这3个好球放在天平左边，把9～11号球放在天平右边，然后称重。此时，会出现3种情况：

（2.1）左边轻，说明可能的情况是9重、10重、11重，共3种可能；

（2.2）平衡，说明可能的情况是9轻、9重，共2种可能。

（2.3）左边重，说明可能的情况是9轻、10轻、11轻，共3种可能。

 

第三次称重：

无论是（1.1）（1.2）（1.3）（2.1）（2.2）（2.3）哪种情况，第三次称重都只需要分辨3种或2种可能，很显然是可以实现的。

 

 

对于上述整个解题过程，吴军博士在《计算之魂》中还绘制了三叉树的解题示意图，方便读者理解并厘清思路。

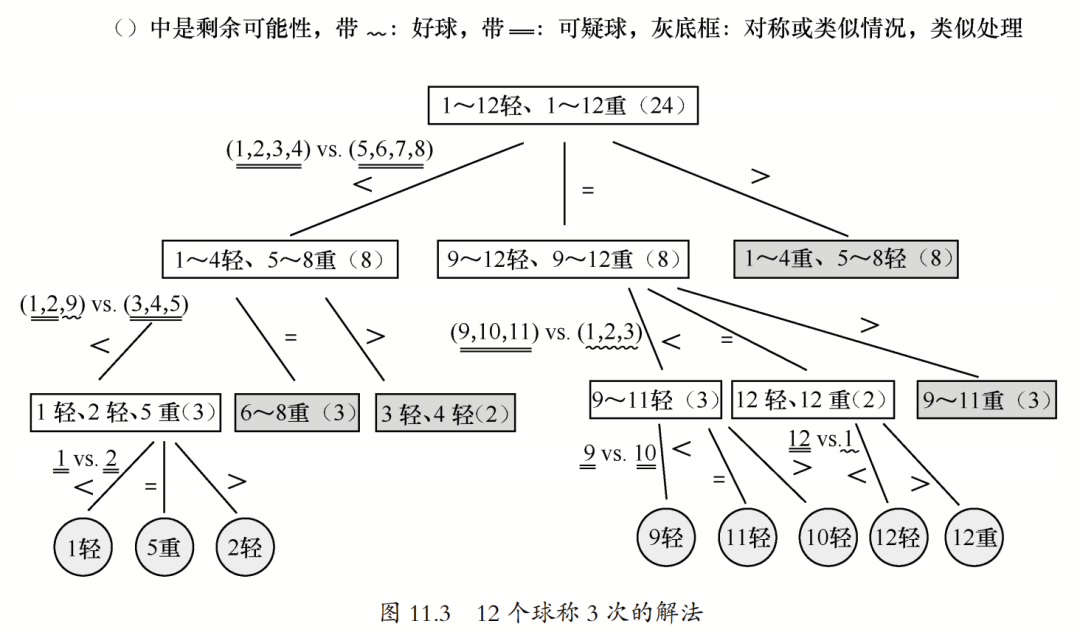
除了解题思路和方法，吴军博士在《计算之魂》中还帮大家梳理了解决这道题所需要躲避的“坑”：

根据第二步的解题分析，我们必须牢记，天平每一次称重最多只能获得1吹特的信息，这是指导我们解题的理论。

也就是说，当还剩1次称重机会时，最多只能区分3种可能；当还剩2次称重机会时，最多只能区分9种情况……如果超过这个界限，必定完成不了任务——这其实就是香农的信息熵理论。

很多人凭直觉，在第一次称球时，把1～6号球放在左边，7～12号球放在右边，这样只会出现左边重或右边重2种可能，即得到1比特而非1吹特的信息。

那么，在这一次称完后，不论是左边重还是右边重，不确定性还有24/2=12种，即若左边轻、右边重，那么12种可能性就是1轻、2轻、……、6轻、7重、8重、…，12重，反过来也是剩下了12种可能性。

接下来你想用2次称重来区分12种信息，就不可能成功——这就是我们需要知道算法的边界在哪里。

理解了上面这些“坑”，我们就知道，在设计每一次称重的时候，都要发挥天平的最大价值，获得3吹特的信息，从而将当前状态的可能性除以3，并确信剩余待确认的可能性是在接下来的称重次数的可验证范围内。

 

《数学之美》《浪潮之巅》作者吴军博士新书《计算之魂》上市，凝结其从事计算机算法和系统设计工作三十年的心得，值得每一位计算机专业的学生以及从业者阅读与思考。

《计算之魂》通过讲解谷歌、微软等头部IT企业的40余道业务与面试题，从递归、编码、分类、组合、图论、分治、存储、并行、状态、随机等10大模块，系统讲解计算机科学和算法的核心知识，并额外提供50余道面试题供读者深入思考。

本书帮助读者掌握计算思维，从“术”的层面获得“道”的提升，从初出茅庐的学生成长为优秀的计算机工程师，非常适合作为“计算机科学”及“算法”的参考读物。 

 

[SoftwareTeacher]

怎么解决一个问题。