231
社区成员
发帖
与我相关
我的任务
分享[基础软件理论与实践] 第五节作业实现 lxr2010
作业信息
作业内容描述：
- Complete the type inference ( two substitution functions )
- Complete the implementation for let-polymorphism
- Think about how to handle recursive functions
作业实现
各作业实现的源代码参见我的代码仓库。
任务1
实现STLC类型推断所需的两个替换函数：实现type_subst函数；实现功能rest[t/x]。
type_subst函数
该函数使用subst列表中的（类型变量名->类型表达式）的映射关系，对类型表达式t中可替换的类型变量名进行替换。
注意到subst列表提供的映射关系只是提供了类型变量之间的等价关系，可能存在部分类型变量，其类型值没有被完全求解。
为了避免多次计算同一个类型变量的值，可以事先对subst列表进行处理，将所有可求解的类型变量进行完全求解。部分类型变量在求解后仍然使用了其他类型变量，则这些变量的类型值是不确定的，需要进行保留。
type_subst函数的实现如下：
let type_subst = (t: typ, s: subst) : typ => {
let rec real_type = (t:typ, s: subst):typ => switch t {
| TInt | TBool => t
| TVar(x) => switch s->Belt.List.getAssoc(x,(a,b)=>a==b) {
| Some(tx) => real_type(tx, s)
| _ => t // might exist variable with no specific type
}
| TArr(t1, t2) => TArr(real_type(t1,s), real_type(t2,s))
}
let s_reduced = {
let mapDict = (d) => {
let (k, st) = d
(k, real_type(st, s))
}
s->Belt.List.map(mapDict)
}
let get_cached_real_type = (x: string): typ => switch s_reduced
->Belt.List.getAssoc(x, (a,b)=>a==b) {
| Some (tx) => tx
| _ => TVar(x)
}
let rec go = (t: typ): typ => switch t {
| TInt | TBool => t
| TVar(x) => get_cached_real_type(x)
| TArr(t1, t2) => TArr(go(t1),go(t2))
}
go(t)
}
实现rest[t/x]
个人将其实现为函数tvar_list_subst，x作为待替换的类型变量名，rest作为约束列表，t作为替换的类型表达式。函数的作用是将约束列表中所有的类型变量x替换为对应的类型表达式t。
注意在替换后列表中可能会出现形如(t1,t1)的约束。这些约束没有实际意义，但是会影响occur函数对类型变量包含关系的判断（occur(t1,t1)=>True），需要删除这种约束，否则会限制类型推断算法的适用范围。
实现如下：
// replace all TVar(x) in type expression s with type t
let rec tvar_subst = (x: string, s: typ, t: typ) : typ => switch s {
| TInt | TBool => s
| TVar(a) if a == x => t
| TVar(_) => s
| TArr(t1, t2) => TArr(tvar_subst(x, t1, t), tvar_subst(x, t2, t))
}
let tvar_list_subst = (x: string, r:constraints, t:typ): constraints => {
let mapDict = (d) => {
let (t1, t2) = d
(tvar_subst(x, t1, t), tvar_subst(x, t2, t))
}
let sameKeyVal = (d) => {
let (t1, t2) = d
(t1 == t2)
}
// remove identical type bindings
r->Belt.List.map(mapDict)->Belt.List.keep((a) => !sameKeyVal(a))
}
任务2
完整实现Let-Polymorphism。
实现的难点主要在inst、gen、free_vars_in_ctx三个函数。
free_vars_in_ctx函数
该函数计算context中的所有自由的类型变量。那么什么是自由的类型变量？我的理解是不受限的变量，即不受Let表达式定义的限制。
在Let表达式Let(h,Fun(f,Let(g,f,g)),h(1))中，按照Let(g,_,_) -> Let(h,_,_)的顺序计算类型变量T_h：
处理
Fun(f,_)，此时context中为{(f,T_f)}；处理
Let(g,f,_)，此时context中仍为{(f,T_f)},按照Let多态规则，g的类型T_g为：
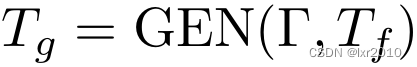
那么T_f是否算作自由变量呢？不算。因为变量f在处理Let(g,f,_)表达式之前被定义，Let多态规则能够generalize的只有在进入Let(g,f,_)后定义的变量，不然就会出现part3 PPT开头提到的unsound generalization的情况。
所以有：
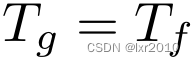
此时context为{(f,T_f),(g,T_g)}
- 处理
Let(g,_,g)，按照Let多态规则，T_g在被使用时会被实例化。设Let表达式中第2个g被实例化的类型为T_g_g，则有：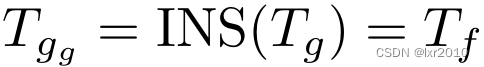
- 处理
Fun(f,Let(g,f,g))，此时函数的类型为：
注意Let(g,f,g)的类型求值已经结束，变量g被移出context。此时context为{(f,T_f)}。
- 处理
Let(h,Fun(f,Let(g,f,g)),_)，按照Let多态规则，h的类型T_h为：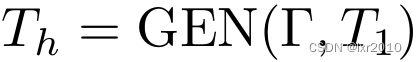
此时Fun(f,_)已经求值完毕，所以也从context中被移除，此时context为{}。这种情况下，T_1表达式中的T_f变量就成为了自由变量，我们在context中找不到它的定义，或者说context中不存在(*,T_f)的项。所以T_f可以被generalize：
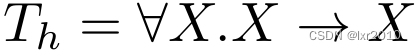
此时context内容为{(h,T_h)}
- 处理
Let(h,_,h(1))，表达式h(1)使用了变量h，根据Let多态规则，T_h需要被实例化，设表达式h(1)中h被实例化的类型为T_h_h(1)，则有：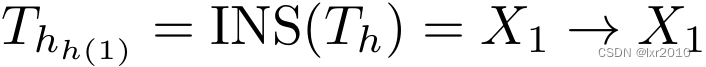
根据App规则，可以求得：
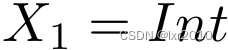
所以
所以在context中寻找自由变量需要进行以下几步：
- 找到context中涉及的所有类型变量；
- 从这些变量中去掉context中已经存在定义的类型变量，对于类型变量
T，如果(*,TVar(Nolink(T)))不存在，则未定义。 - 剩下的就是自由变量
inst函数
inst函数实现的思路也比较类似。处理类型T时，需要先找出所有的QVar表达式，去除重复项，再对这些QVar表达式每个生成对应的一个实例化类型，保存在map中。使用与任务1中type_subst类似的方法对类型T中的QVar表达式进行替换。
gen函数
使用直观方法实现Let Polymorphism时，generalization遇到TVar(Nolink(xs))表达式时需要特别注意。context中出现的自由类型变量需要generalize；如果类型变量在context中没有定义，也需要generalize；如果类型变量在subst列表中出现，说明在前面的处理过程中已经将对应变量generalized，需要将变量替换为subst列表提供的相应类型表达式。generalize后，需要在subst列表中添加新的映射关系，传递给后面的处理过程。
使用Level Based Let Polymorphism方法实现时，prune_level函数需要保证被修改的类型变量ty中所有涉及到TVar(Nolink(_,lv))的项，lv的值不超过参数提供的level，这样做是为了能够保证基于level正确判断变量是否为自由变量。Level-based实现方法见任务3。
直观方法的完整实现如下：
module LetPoly = {
type rec typ = TInt | TBool| TVar(ref<tvar>) | TArr(typ, typ) | QVar(string)
and tvar = Nolink(string) | Linkto(typ)
type rec expr = CstI(int) | CstB(bool) | Var(string)
| If(expr, expr, expr)
| Add(expr, expr)
| Fun(string, expr) | App(expr, expr)
| Let(string, expr, expr)
let rec toString = (t: typ) => switch t {
| TInt => "Int"
| TBool => "Bool"
| TVar(x) => switch x.contents {
| Nolink(sx) => "T_"++sx
| Linkto(tx) => toString(tx)
}
| TArr(x,y) => "( " ++ toString(x) ++ " -> " ++ toString(y) ++ " )"
| QVar(s) => "QT_"++s
}
let tvar_cnt = ref(0)
let fresh_name = (): ref<tvar> => {
tvar_cnt.contents = tvar_cnt.contents + 1
ref(Nolink("@*"++Js.Int.toString(tvar_cnt.contents)))
}
let new_tvar = () : typ => TVar(fresh_name())
let inst_map = ref(list{})
let fresh_inst = (qs: string) : ref<tvar> => {
let inst_cnt = switch inst_map.contents->Belt.List.getAssoc(qs, (a,b)=>a==b) {
|Some (n) => n
|None => 0
}
inst_map.contents = Belt.List.setAssoc(inst_map.contents, qs, inst_cnt+1, (a,b)=>a==b)
ref(Nolink(qs ++ "_" ++ Js.Int.toString(inst_cnt+1)))
}
let new_inst = (qs: string) :typ => TVar(fresh_inst(qs))
let inst = (tp: typ):typ => {
let rec get_qvars = (t: typ) : list<string> => {
switch t {
| TInt | TBool => list{}
| TVar(x) => switch x.contents {
| Nolink(_) => list{}
| Linkto(rv) => get_qvars(rv)
}
| TArr(x, y) => Belt.List.concatMany([get_qvars(x), get_qvars(y)])
| QVar(qs) => list{qs}
}
}
let qvars = tp->get_qvars->Belt.List.toArray->Belt.Set.String.fromArray->Belt.Set.String.toList
let subst_map = qvars->Belt.List.map(qs=>(qs,new_inst(qs)))
let rec subst_inst = (t: typ, m:list<(string,typ)>) : typ => switch t {
| TInt | TBool => t
| TVar(x) => switch x.contents {
| Nolink(_) => t
| Linkto(rv) => subst_inst(rv, m)
}
| TArr(x, y)=> TArr(subst_inst(x,m), subst_inst(y,m))
| QVar(qs) => switch m->Belt.List.getAssoc(qs, (a,b)=>a==b) {
| Some(r) => r
| _ => assert false
}
}
subst_inst(tp, subst_map)
}
// tell if TVar(x) is in type expression t
let rec occurs = (x: ref<tvar>,t: typ) : bool => switch t {
| TInt | TBool => false
| TVar(a) if a.contents == x.contents => true
| TVar(b) => switch b.contents {
| Linkto(t') => occurs(x, t')
| _ => false
}
| TArr(t1, t2) => occurs(x, t1) || occurs(x, t2)
| QVar(_) => false
}
let rec repr_type = (t:typ): typ => {
switch t {
| TVar(tvar: ref<tvar>) => switch tvar.contents {
| Nolink(_) => t
| Linkto(t1) => {
let t1' = repr_type(t1)
tvar := Linkto(t1')
t1'
}
}
| _ => t
}
}
let rec unify = (t1: typ, t2: typ) : unit => {
let t1' = repr_type(t1) and t2' = repr_type(t2)
if t1' === t2' { () }
else {
switch (t1', t2') {
| (TInt, TInt) | (TBool, TBool) => ()
| (TArr(t1, t2),TArr(t3,t4)) => {
unify(t1,t3)
unify(t2,t4)
}
| (TVar(tvar), t) | (t, TVar(tvar)) => {
if occurs(tvar,t) {
Js.log("Can't solve these constraints")
assert false
}
tvar := Linkto(t)
}
| _ => {
Js.log("Wrong constraint : ("++ t1'->toString ++ "," ++ t2'->toString ++")" )
assert false
}
}
}
}
type context = list<(string, typ)>
type subst = list<(string, typ)>
let toStringSubst = (s: subst) => {
let mapDictToString = (d:(string, typ)) => {
let (x, t) = d
x ++ " |-> " ++ t->toString
}
switch s {
| list{} => ""
| list{h, ...rest} => List.fold_left((a,b)=>a++","++b->mapDictToString, h->mapDictToString, rest)
}
}
//context will change when finished a let expression,
// definitions inside the let expression will be removed from context.
// Therefore those type variables whose definition cann't be found
// in context are free type variables
let map_definition = (p : (string, typ)) => switch p {
| (_ , TVar(x)) => switch x.contents {
| Nolink(xs) => Some(xs)
| _ => None
}
| _ => None
}
let free_tvars_in_ctx = (ctx : context): list<string> => {
let rec get_tvar_nolink_in_typ = (t: typ) : list<string> => switch t {
| TBool | TInt => list{}
| TVar(x) => switch x.contents {
| Nolink(xs) => list{xs}
| Linkto(xt) => get_tvar_nolink_in_typ(xt)
}
| TArr(x, y) => Belt.List.concatMany([get_tvar_nolink_in_typ(x), get_tvar_nolink_in_typ(y)])
| QVar(_) => assert false // Rank-1 polymorphism restriction
}
let getKey = (p: (string,typ)) => {
let (_ , k) = p
k
}
// deduplicate list using Belt.Set.String, prepare to make diff between tvar_definitions
let tvar_nolink = ctx->Belt.List.map(p=>p->getKey->get_tvar_nolink_in_typ->Belt.List.toArray)->
Belt.List.toArray->Belt.Array.concatMany->
Belt.Set.String.fromArray
let tvar_definitions = ctx->Belt.List.keepMap(map_definition)->Belt.List.toArray->Belt.Set.String.fromArray
let undefined_tvar = tvar_nolink->Belt.Set.String.diff(tvar_definitions)->Belt.Set.String.toList
undefined_tvar
}
let gen = (ty: typ, ctx: context) : typ => {
let freetvars = free_tvars_in_ctx(ctx)
let rec go = (ty:typ , subst:subst): (typ,subst) => switch ty {
| TInt | TBool => (ty,subst)
| TVar(x) => switch x.contents {
| Nolink(xs) => switch subst->Belt.List.getAssoc(xs,(a,b)=>a==b) {
| Some(qt) => (qt,subst)
| None => {
// xs is not a free type var in context.
// find xs in context to check whether it is constrained.
switch ctx->Belt.List.keepMap(map_definition)->Belt.List.has(xs,(a,b)=>a==b) {
| true => (ty,subst) // constrained by context. don't change
| false => {
// unconstrained type variable. Generalize it and add to subst list.
(QVar(xs),list{(xs,QVar(xs)),...subst})
}
}
}
}
| Linkto(xt) => {
let (xt', subst') = go(xt, subst)
(TVar(ref(Linkto(xt'))),subst')
}
}
| TArr(x, y) => {
let (x', subst') = go(x, subst)
let (y', subst'') = go(y, subst')
(TArr(x',y'),subst'')
}
| QVar(_) => assert false // Rank-1 polymorphism restriction
}
let (fst,_) = go(ty, freetvars->Belt.List.map(x=>(x,QVar(x))))
fst
}
let rec check_expr = (ctx: context, expr: expr) : typ =>
switch expr {
| CstI(_) => TInt
| CstB(_) => TBool
| Var(s) => switch ctx->Belt.List.getAssoc(s,(a,b)=>a==b) {
| Some (ts) => inst(ts)
| _ => assert false // As for well-formed expr, no Var is used before declaration
}
| If(cond, bTrue, bFalse) => {
let tx = new_tvar()
let t1 = check_expr(ctx, cond)
let t2 = check_expr(ctx, bTrue)
let t3 = check_expr(ctx, bFalse)
unify(t1, TBool)
unify(t2,tx)
unify(t3,tx)
tx
}
| Fun(x, e) => {
let tx = new_tvar()
let te = check_expr(list{(x, tx), ...ctx}, e)
TArr(tx, te)
}
| App(e1, e2) => {
let tx = new_tvar()
let t1 = check_expr(ctx, e1)
let t2 = check_expr(ctx, e2)
unify(t1, TArr(t2,tx))
tx
}
| Add(e1, e2) => {
let tx = new_tvar()
let t1 = check_expr(ctx, e1)
let t2 = check_expr(ctx, e2)
unify(tx,TInt)
unify(t1,TInt)
unify(t2,TInt)
tx
}
| Let(x, e1, e2) => {
let t1 = check_expr(ctx, e1)
let ctx' = list{(x, gen(t1, ctx)), ...ctx}
let t2 = check_expr(ctx', e2)
Js.log(ctx'->toStringSubst)
t2
}
}
let infer = (expr: expr) : typ => {
let t = check_expr(list{}, expr)
t
}
let test = Let("h",Fun("f",Let("g",Var("f"),Var("g"))),If(App(Var("h"),CstB(true)),App(Var("h"),CstI(1)),App(Var("h"),CstI(0))))
let inferred = infer(test)
Js.log(inferred->toString)
}
测试结果如下：
g |-> T_@*1,f |-> T_@*1
h |-> ( QT_@*1 -> QT_@*1 )
Int
任务3
尝试为Let-Polymorphism的实现添加对递归函数的支持。类似第4节作业的想法，在Let(x,e1,e2)表达式的类型求值中，为变量x绑定一个新的类型变量T_x，并将映射(x,T_x)添加到e1求值的context中，T_x的level应该与e1求值的level相同。此外还需要添加类型约束
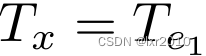
包含递归函数支持的Level-based Let Polymorphism完整实现如下：
module LvLetPoly = {
type rec typ = TInt | TBool | TArr(typ, typ) | TVar(ref<tvar>) | QVar(string)
and tvar = Nolink(string,int) | Linkto(typ)
type rec expr = CstI(int) | CstB(bool) | Var(string)
| If(expr, expr, expr)
| Add(expr, expr)
| Mul(expr, expr)
| Leq(expr, expr)
| Fun(string, expr) | App(expr, expr)
| Let(string, expr, expr)
let rec toStringE= (e: expr) => switch e {
| CstI(i) => Js.Int.toString(i)
| CstB(b) => if b {"True"} else {"False"}
| Var(s) => s
| If(c, e1, e2) => "If (" ++ c->toStringE ++ ") then { " ++ e1->toStringE ++ " } else { " ++ e2->toStringE ++ " }"
| Add(e1, e2) => "( " ++ e1->toStringE ++ "+" ++ e2->toStringE ++ " )"
| Mul(e1, e2) => "( " ++ e1->toStringE ++ "*" ++ e2->toStringE ++ " )"
| Leq(e1, e2) => e1->toStringE ++ "<=" ++ e2->toStringE
| Fun(x, e) => "fun " ++ x ++ " -> " ++ e->toStringE
| App(e1, e2) => "( " ++ e1->toStringE ++ " )( " ++ e2->toStringE ++ " )"
| Let(x, e1, e2) => "let " ++ x ++ " = " ++ e1->toStringE ++ " in " ++ e2->toStringE
}
let rec toString = (t: typ) => switch t {
| TInt => "Int"
| TBool => "Bool"
| TVar(x) => switch x.contents {
| Nolink(sx,lv) => "T" ++Js.Int.toString(lv) ++ "_"++sx
| Linkto(tx) => toString(tx)
}
| TArr(x,y) => "( " ++ toString(x) ++ " -> " ++ toString(y) ++ " )"
| QVar(s) => "QT_"++s
}
let tvar_cnt = ref(0)
let fresh_name = (): string => {
tvar_cnt.contents = tvar_cnt.contents + 1
"@*"++Js.Int.toString(tvar_cnt.contents)
}
let new_tvar = (level:int) : typ => TVar(ref(Nolink(fresh_name(),level)))
let inst_map = ref(list{})
let fresh_inst = (qs: string) : string => {
let inst_cnt = switch inst_map.contents->Belt.List.getAssoc(qs, (a,b)=>a==b) {
|Some (n) => n
|None => 0
}
inst_map.contents = Belt.List.setAssoc(inst_map.contents, qs, inst_cnt+1, (a,b)=>a==b)
qs ++ "_" ++ Js.Int.toString(inst_cnt+1)
}
let new_inst = (qs: string, level:int) :typ => TVar(ref(Nolink(fresh_inst(qs),level)))
// tell if TVar(x) is in type expression t
let rec occurs = (x: ref<tvar>,t: typ) : bool => switch t {
| TInt | TBool => false
| TVar(a) if a.contents == x.contents => true
| TVar(b) => switch b.contents {
| Linkto(t') => occurs(x, t')
| _ => false
}
| TArr(t1, t2) => occurs(x, t1) || occurs(x, t2)
| QVar(_) => false
}
let rec repr_type = (t:typ): typ => {
switch t {
| TVar(tvar: ref<tvar>) => switch tvar.contents {
| Nolink(_,_) => t
| Linkto(t1) => {
let t1' = repr_type(t1)
tvar := Linkto(t1')
t1'
}
}
| _ => t
}
}
let get_level = (tvar: ref<tvar>) : option<int> => switch tvar.contents {
| Nolink(_, lv) => Some(lv)
| _ => assert false
}
// make sure all tvars' level equal or smaller than level
let prune_level = (level: option<int>, ty: typ):() => {
let rec checker = (t: typ, lv: int) => switch t {
| TInt | TBool => ()
| TVar(x) => switch x.contents {
| Nolink(xs, l) if (l > lv) => {
x.contents = Nolink(xs, lv)
}
| Linkto(xt) => checker(xt, lv)
| _ => ()
}
| TArr(x, y) => {
checker(x, lv)
checker(y, lv)
}
| QVar(_) => ()
}
switch level {
| Some(l) => checker(ty, l)
| _ => ()
}
}
let rec unify = (t1: typ, t2: typ) : unit => {
let t1' = repr_type(t1) and t2' = repr_type(t2)
if t1' === t2' { () }
else {
switch (t1', t2') {
| (TInt, TInt) | (TBool, TBool) => ()
| (TArr(t1, t2),TArr(t3,t4)) => {
unify(t1,t3)
unify(t2,t4)
}
| (TVar(tvar), t) | (t, TVar(tvar)) => {
// tvar must be form Nolink(_,_)
if occurs(tvar,t) {
Js.log("Can't solve these constraints")
assert false
}
prune_level(get_level(tvar),t)
tvar := Linkto(t)
}
| _ => {
Js.log("Wrong constraint : ("++ t1'->toString ++ "," ++ t2'->toString ++")" )
assert false
}
}
}
}
type context = list<(string, typ)>
type subst = list<(string, typ)>
let toStringSubst = (s: subst) => {
let mapDictToString = (d:(string, typ)) => {
let (x, t) = d
x ++ " |-> " ++ t->toString
}
switch s {
| list{} => ""
| list{h, ...rest} => List.fold_left((a,b)=>a++","++b->mapDictToString, h->mapDictToString, rest)
}
}
let inst = (ty: typ, level: int) : typ => {
let rec get_qvars = (t: typ) : list<string> => {
switch t {
| TInt | TBool => list{}
| TVar(x) => switch x.contents {
| Nolink(_,_) => list{}
| Linkto(rv) => get_qvars(rv)
}
| TArr(x, y) => Belt.List.concatMany([get_qvars(x), get_qvars(y)])
| QVar(qs) => list{qs}
}
}
let qvars = ty->get_qvars->Belt.List.toArray->Belt.Set.String.fromArray->Belt.Set.String.toList
let subst_map = qvars->Belt.List.map(qs=>(qs,new_inst(qs,level)))
let rec subst_inst = (t: typ, m:list<(string,typ)>) : typ => switch t {
| TInt | TBool => t
| TVar(x) => switch x.contents {
| Nolink(_,_) => t
| Linkto(rv) => subst_inst(rv, m)
}
| TArr(x, y)=> TArr(subst_inst(x,m), subst_inst(y,m))
| QVar(qs) => switch m->Belt.List.getAssoc(qs, (a,b)=>a==b) {
| Some(r) => r
| _ => assert false
}
}
subst_inst(ty, subst_map)
}
let gen = (ty: typ, level: int) : typ => {
let rec go = (t: typ) : typ => switch t {
| TInt | TBool => t
| TVar(x) => switch x.contents {
| Nolink (xs, xlv) if xlv > level => {
QVar(xs)
}
| Nolink (_, _) => t
| Linkto(xt) => {
let xt' = go(xt)
TVar(ref(Linkto(xt')))
}
}
| TArr(x,y) => {
TArr(go(x),go(y))
}
| QVar(_) => assert false // Rank-1 polymorphism restriction
}
let fst = go(ty)
fst
}
let rec check_expr = (ctx: context, expr: expr, level: int) : typ => {
let res = switch expr {
| CstI(_) => TInt
| CstB(_) => TBool
| Var(s) => switch ctx->Belt.List.getAssoc(s,(a,b)=>a==b) {
| Some (ts) => inst(ts, level)
| _ => assert false // As for well-formed expr, no Var is used before declaration
}
| If(cond, bTrue, bFalse) => {
let tx = new_tvar(level)
let t1 = check_expr(ctx, cond, level)
let t2 = check_expr(ctx, bTrue, level)
let t3 = check_expr(ctx, bFalse, level)
unify(t1, TBool)
unify(t2,tx)
unify(t3,tx)
tx
}
| Fun(x, e) => {
let tx = new_tvar(level)
let te = check_expr(list{(x, tx), ...ctx}, e, level+1)
TArr(tx, te)
}
| App(e1, e2) => {
let tx = new_tvar(level)
let t1 = check_expr(ctx, e1, level)
let t2 = check_expr(ctx, e2, level)
unify(t1, TArr(t2,tx))
tx
}
| Add(e1, e2) | Mul(e1, e2) => {
let tx = new_tvar(level)
let t1 = check_expr(ctx, e1, level)
let t2 = check_expr(ctx, e2, level)
unify(tx,TInt)
unify(t1,TInt)
unify(t2,TInt)
tx
}
| Leq(e1,e2) => {
let tx = new_tvar(level)
let t1 = check_expr(ctx, e1, level)
let t2 = check_expr(ctx, e2, level)
unify(tx, TBool)
unify(t1, TInt)
unify(t2, TInt)
tx
}
| Let(x, e1, e2) => {
let tx = new_tvar(level+1)
let t1 = check_expr(list{(x,tx),...ctx}, e1, level+1)
let ctx' = list{(x, gen(t1, level)), ...ctx}
let t2 = check_expr(ctx', e2, level)
unify(tx, t1)
Js.log(ctx'->toStringSubst)
t2
}
}
res
}
let infer = (expr: expr) : typ => {
let t = check_expr(list{}, expr, 0)
t
}
}
module Test = {
open! LvLetPoly
let test0 = Let("h",Fun("f",Let("g",Var("f"),Var("g"))),If(App(Var("h"),CstB(true)),App(Var("h"),CstI(1)),App(Var("h"),CstI(0))))
let fact = Let("fac",
Fun("n",If(Leq(Var("n"),CstI(0)),
CstI(1),
Mul(Var("n"),App(Var("fac"),Add(Var("n"),CstI(-1)))))),
App(Var("fac"),CstI(5)))
let more_fact = Let("facc",
Fun("m",Fun("n",If(Leq(Var("n"),CstI(0)),
Var("m"),
App(App(Var("facc"),Var("m")),Add(Var("n"),CstI(-1)))))),
Var("facc"))
let tests = list{
test0, fact, more_fact
}
let run_test = (ts: list<expr>) : () => {
ts->Belt.List.forEach(t=>{
Js.log("Expr: " ++ t->toStringE)
let inferred = infer(t)
Js.log(inferred->toString)
})
}
let run = () => {
let _ = run_test(tests)
}
}
Test.run()
测试结果如下：
Expr: let h = fun f -> let g = f in g in If (( h )( True )) then { ( h )( 1 ) } else { ( h )( 0 ) }
g |-> T1_@*2,f |-> T1_@*2,h |-> T1_@*1
h |-> ( QT_@*2 -> QT_@*2 )
Int
Expr: let fac = fun n -> If (n<=0) then { 1 } else { ( n*( fac )( ( n+-1 ) ) ) } in ( fac )( 5 )
fac |-> ( Int -> Int )
Int
Expr: let facc = fun m -> fun n -> If (n<=0) then { m } else { ( ( facc )( m ) )( ( n+-1 ) ) } in facc
facc |-> ( QT_@*19 -> ( Int -> QT_@*19 ) )
( T0_@*19_1 -> ( Int -> T0_@*19_1 ) )
其中T0_@*19_1表示由generalized变量QT_@*19第1次实例化产生的类型，类型level为0。
...全文
请发表友善的回复…
发表回复
SoftwareTeacher 2023-03-17
精选
- 打赏
- 举报
5.00元
赞认真完成作业的同学！
