蓝桥杯 Day 7 （C++）

[Dream-Y.ocean]

星期计算

#include <iostream>

using namespace std;

// 快速幂
// 求 a ^ k % p
// 【因为每过7天的星期几都是一样的，所以可以 mol 7】
long long qmi(int a, int k, int p)
{
    long long ans = 1 % p; 

    while(k)
    {
        if(k & 1) ans = ans * a % p;
        k >>= 1;
        a = (long long)a * a % p;
    }
    return ans;
}

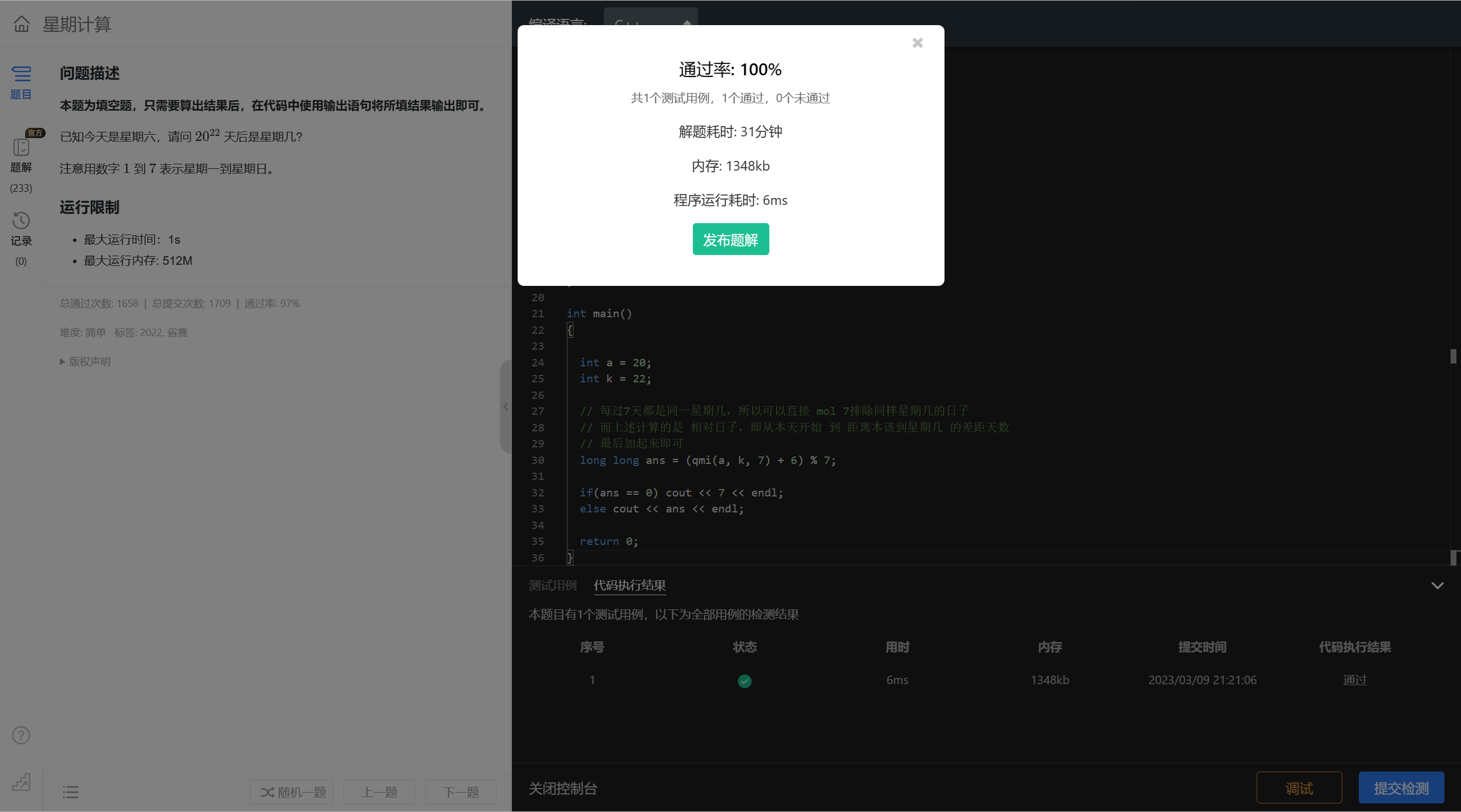
int main()
{

    int a = 20;
    int k = 22;

    // 每过7天都是同一星期几，所以可以直接 mol 7排除同样星期几的日子
    // 而上述计算的是 相对日子，即从本天开始 到 距离本该到星期几 的差距天数
    // 最后加起来即可
    long long ans = (qmi(a, k, 7) + 6) % 7;

    if(ans == 0) cout << 7 << endl;
    else cout << ans << endl;

    return 0;
}

考勤刷卡

#include <iostream>
#include <string>
#include <set>

using namespace std;

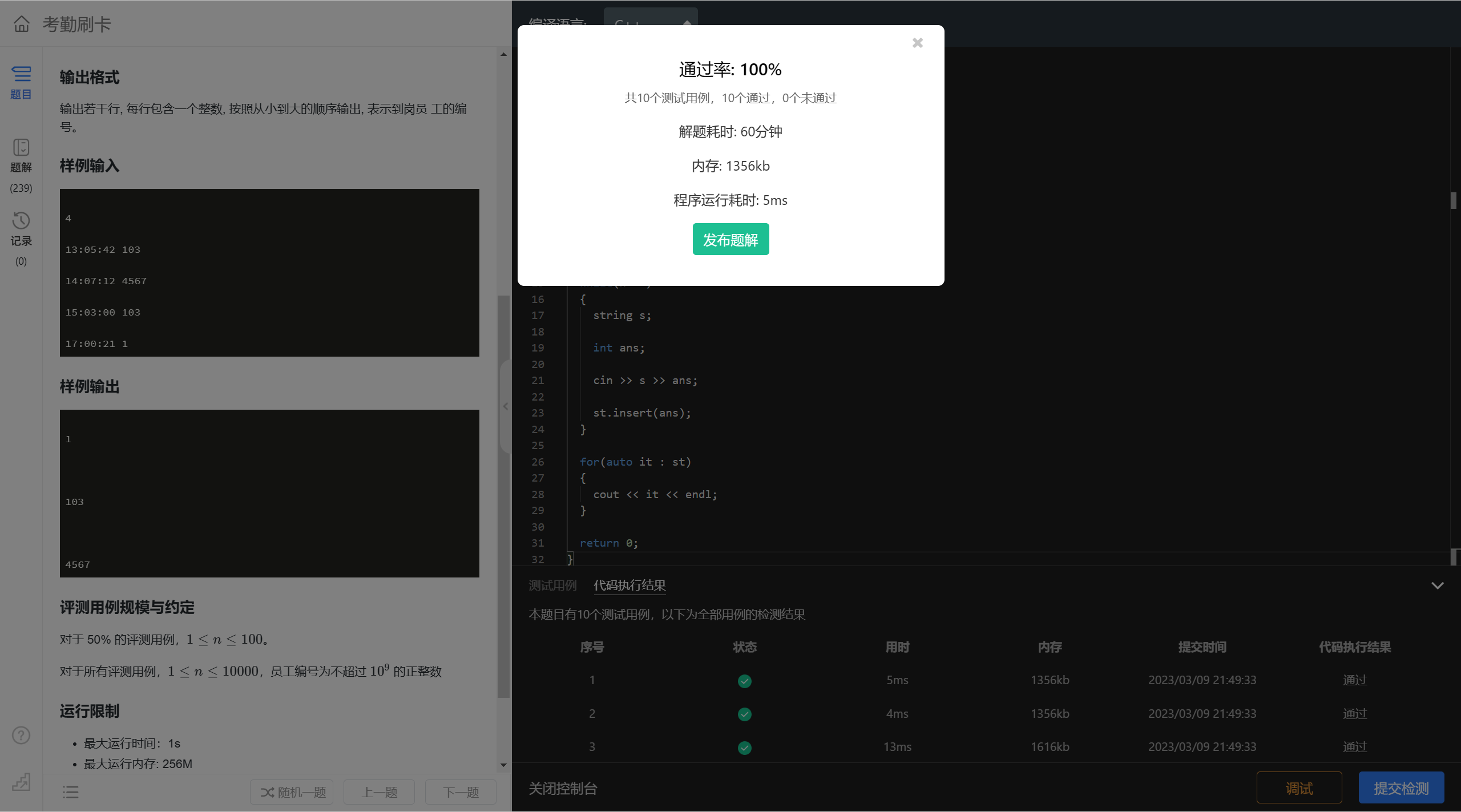
int n;

int main()
{
    cin >> n;

    set<int> st;

    while(n --)
    {
        string s;
        
        int ans;

        cin >> s >> ans;

        st.insert(ans);
    }

    for(auto it : st)
    {
        cout << it << endl;
    }

    return 0;
}

卡片

#include <iostream>

using namespace std;

int n;

// 1 -> (1,1) - 1
// 2 -> (1,1)(1,2)(2,2) - 3 - 1 = 2
// 3 -> (1,1)(1,2)(1,3)(2,2)(2,3)(3,3) - 6 - 3 = 3
// 4 -> (1,1)(1,2)(1,3)(1,4)(2,2)(2,3)(2,4)(3,3)(3,4)(4,4) - 10 - 6 = 4

// 从上述规律可看出：每多一种卡牌，卡牌所能 多 表示的人数 = 当前卡牌种类

// 思路：枚举牌数的种类，我们记下来 截至 当前排数所能表示的人数，直至 表示的人数 >= n
//         此时的牌数种类 就是 ans

int main()
{
    cin >> n;

    int ans = 1;

    int sum = 1;

    while(sum < n)
    {
        ans ++;
        sum += ans;
    }

    cout << ans << endl;

    return 0;
}