BUAA_OO_2023 第一单元总结

李子锐-21373337 学生 2023-03-19 16:18:26

BUAA_OO_2023 第一单元总结

BUAA_OO_2023 第一单元总结
前言
一、第一次作业
1.1 作业内容
1.2 程序结构
1.2.1 类与类图
1.2.2 递归下降算法
1.3 设计思路
1.4 分析评估
1.4.1 度量分析
1.4.2 架构分析
1.4.3 bug分析
二、第二次作业
2.1 作业内容
2.2 程序结构
2.3 设计思路
2.4 分析评估
2.4.1 度量分析
2.4.2 架构分析
2.4.3 bug分析
三、第三次作业
3.1 作业内容
3.2 程序结构
3.3 设计思路
3.4 分析评估
3.4.1 度量分析
3.4.2 架构分析
3.4.3 bug分析
四、互测策略
五、架构设计体验&心得体会

前言

第一单元针对括号拆分、表达式化简进行迭代，帮助同学们理解Java的基本语法、递归下降思想、面向对象思想等。

一、第一次作业

1.1 作业内容

第一次作业的任务是针对一个由x，y，z三种变量，通过加、减、乘、幂次、还有括号构成的表达式的建模和展开。下面是作业的形式化表达:

表达式 → 空白项 [加减空白项] 项空白项 | 表达式加减空白项项空白项
项 → [加减空白项] 因子 | 项空白项 '*' 空白项因子
因子 → 变量因子 | 常数因子 | 表达式因子
变量因子 → 幂函数
常数因子 → 带符号的整数
表达式因子 → '(' 表达式 ')' [空白项指数]
幂函数 → ('x' | 'y' | 'z') [空白项指数]
指数 → '**' 空白项 ['+'] 允许前导零的整数 (注：指数一定不是负数)
带符号的整数 → [加减] 允许前导零的整数
允许前导零的整数 → ('0'|'1'|'2'|…|'9'){'0'|'1'|'2'|…|'9'}
空白项 → {空白字符}
空白字符 → （空格） | \t
加减 → '+' | '-'
1.2 程序结构

1.2.1 类与类图

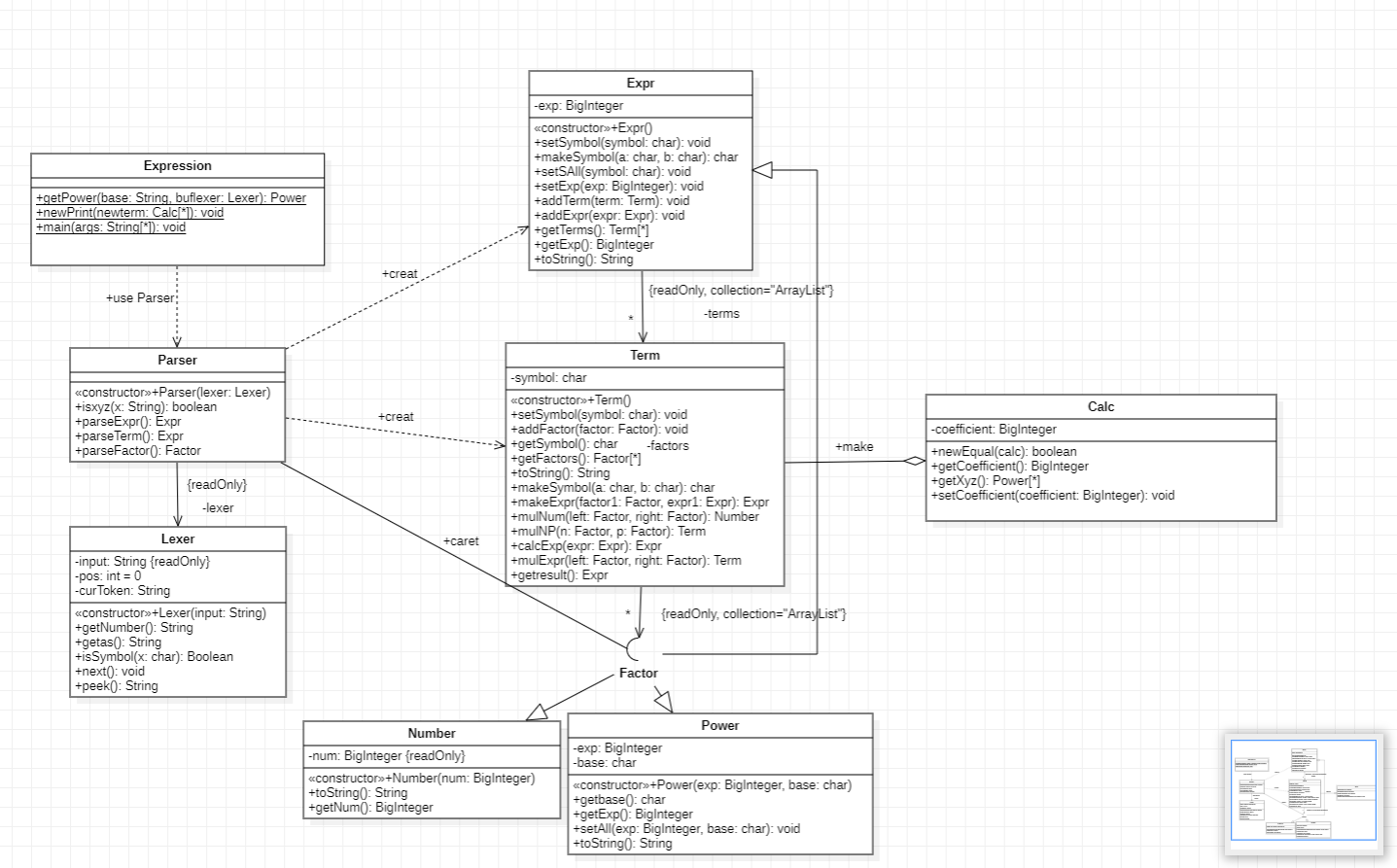
第一次作业较为简单，需要完成的类较少。在完成作业时，我基于实验和提示中的递归下降算法完成本次作业。下面介绍类图中出现的类。

Factor: 接口统一管理所有因子。
Number: 常数因子，实现了Factor接口。
Power: 变量因子，在这次作业中为幂函数,实现了Factor接口。
Expr: 表达式(因子)，在作业中我将读入的字符串视为一个指数为1的表达式因子,同样实现了Factor接口。
Term: 项，由因子组成，即Arraylist。
Calc: 用于加减时合并同类项，形式为 $系数\times x^{m_1}y^{m_2}z^{m_3}$。
Parser、lexer：语法分析器、词法分析器，在总结递归下降算法时详解。
1.2.2 递归下降算法
递归下降算法是一种按照特定的文法结构解析字符串的有效方法，是一种自顶向下的算法。在第一单元作业中，递归下降是我的设计中主要解析字符串的工具。具体通过Parser(语法分析器)和Lexer(词法分析器)实现。

在Parser中有Lexer属性，Lexer负责把字符串拆成一个个子串提供给Parser，辅助Parser识别子串。在读入表达式后，使用Parser根据Lexer解析的子串，调用对应的Parser方法，构造Expr、Term、fatror等对象。
1.3 设计思路

对于本次的作业的乘法化简，我选择在递归过程中进行，在parseTerm()方法得到一个新的Term时，对Term进行乘法运算，将乘法运算得到的表达式作为parseTerm()的返回值，这样最后解析得到的表达式会是一个不含Expr因子的Term的集合。
对于本次作业的加法化简，我在整个表达式解析完后进行，为解决加法合并问题，我将Expr中的Term格式化为了Calc形式，即 $系数\times x^{m_1}y^{m_2}z^{m_3}$。这样合并时只需要依次比较所有Calc的xyz的幂次即可。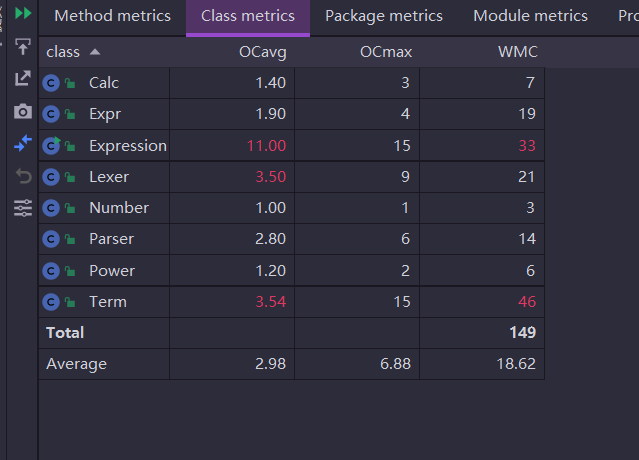
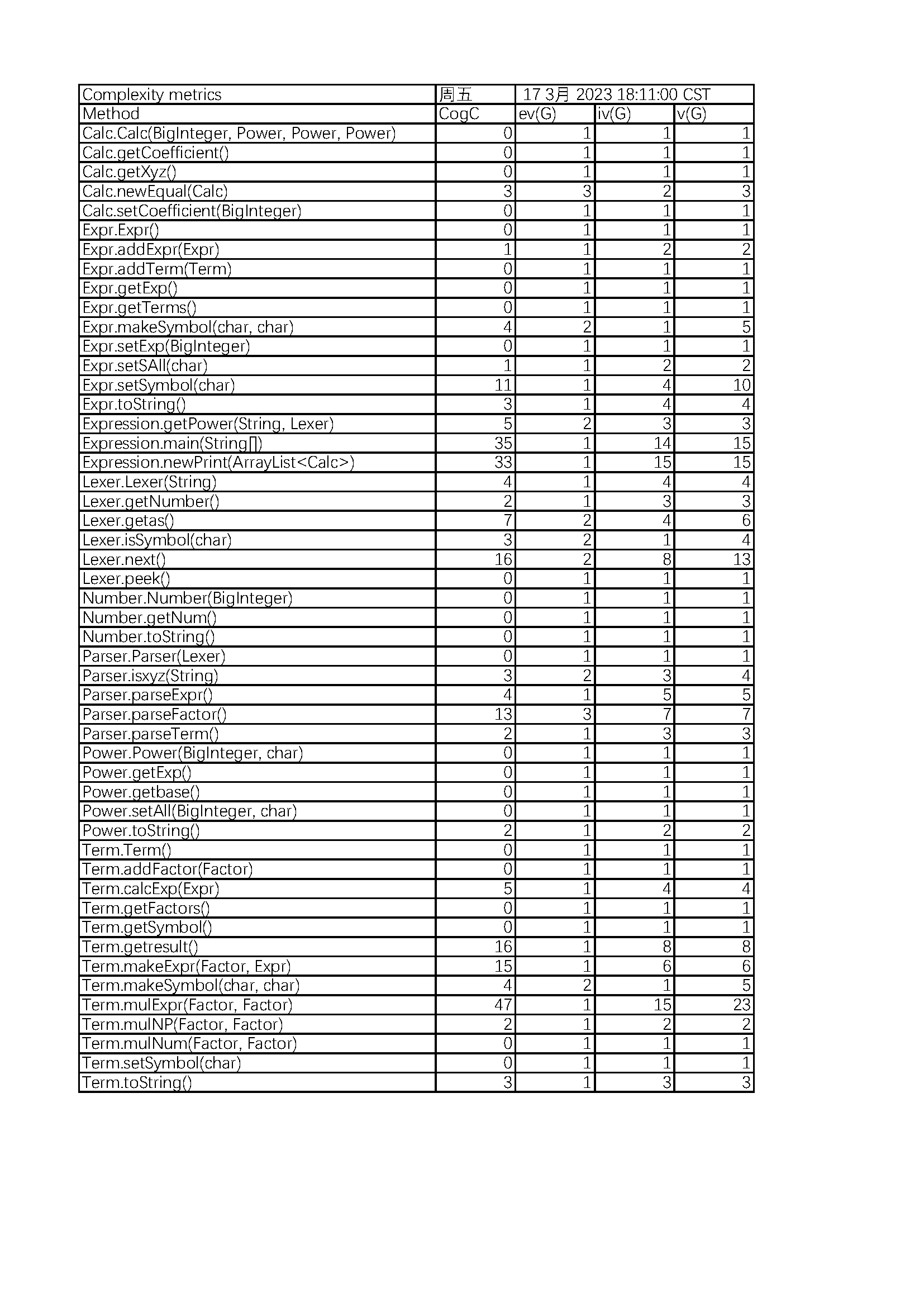
1.4 分析评估

1.4.1 度量分析

从度量分析可以看出复杂度主要集中在Expression、Lexer、Term三个类中，究其原因是这三个类中方法设计的不合理，出现了许多巨型方法。特别是为了图方便，在主函数中写了过多方法。

1.4.2 架构分析

加法的化简在主函数里实现，乘法的化简在Term中实现，使架构较为臃肿，应该将这两个抽象为一个工具类。
在方法mulExpr中实现了多个if语句，使该方法成为了巨型方法，应该将该方法作为一个入口，具体实现细节应该在多个不同的方法中实现。
在第一次作业中，Expr中是Term的容器，但最后化简和输出是要使用的Calc容器，代码缺乏统一性。
1.4.3 bug分析
在第一次作业中，我由于不熟悉课程机制，课下弱测通过后并未做过多测试，导致出现了许多低级错误，如x**0=0和负的常数因子无法识别符号等。两个bug分别出现在newprint和parseFactor方法中，两个的圈复杂度分别为7和15，均高于平均值。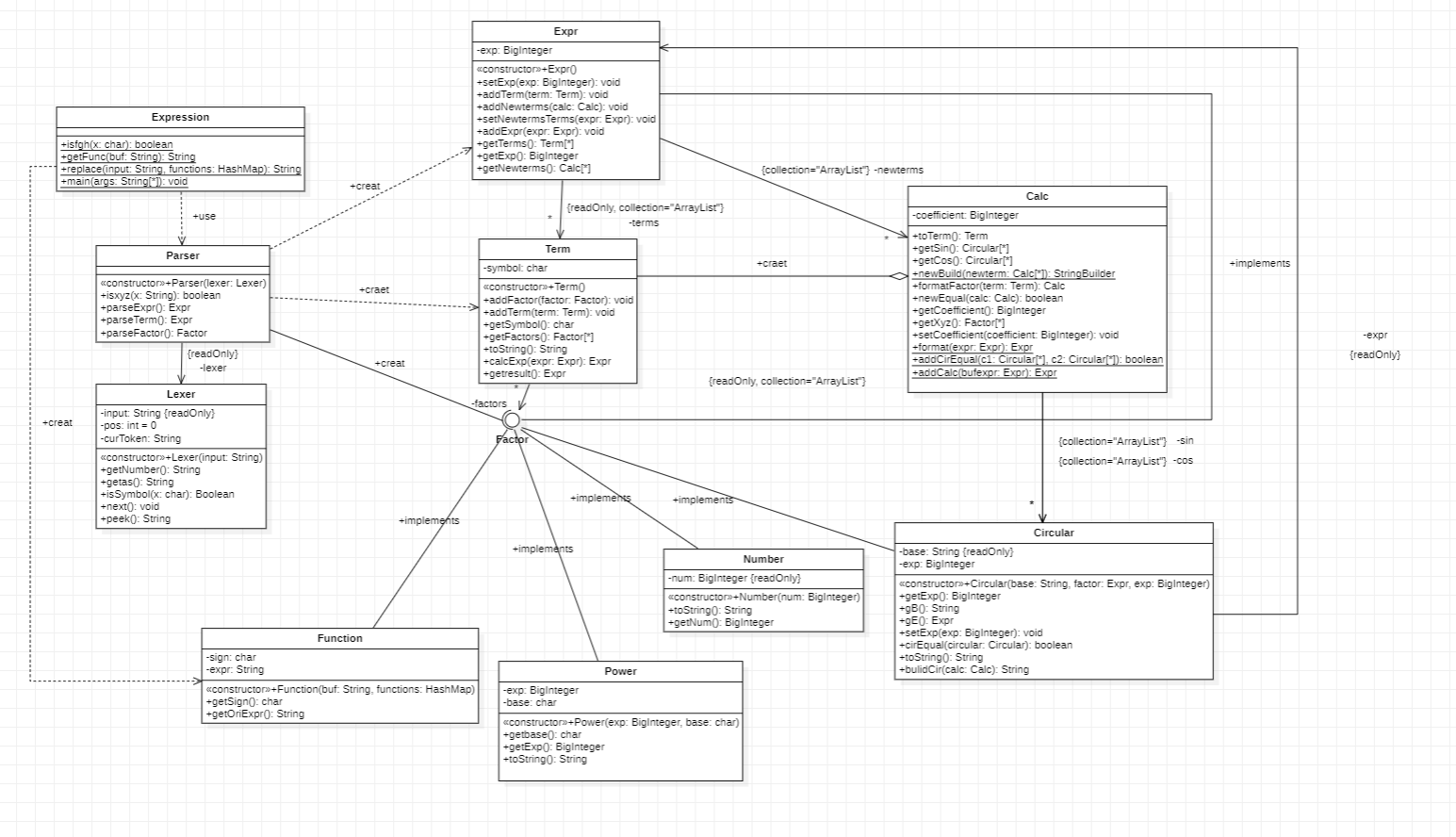
在互测过程中发现的bug主要有符号处理问题、空格处理问题和前导0问题，这些问题的发生均与字符串层面的处理有着很大的关系，不少同房的人理所当然地假定了字符串的下一个字符，导致程序抛出异常。总而言之，字符串层面的处理具有巨大风险，应该尽量避免使用，若不得不进行这些操作，也应该多加测试。
二、第二次作业

2.1 作业内容
第二次作业增加了括号嵌套，三角函数和自定义函数调用，因为我使用的是递归下降算法，在第一次作业时就完成了嵌套括号的处理，所以我本次作业的主要任务就是完成三角函数和自定义函数调用。下面是新增的形式表达:

三角函数 → 'sin' 空白项 '(' 空白项因子空白项 ')' [空白项指数] | 'cos' 空白项 '(' 空白项因子空白项 ')' [空白项指数]
自定义函数定义 → 自定义函数名空白项 '(' 空白项自变量空白项 [',' 空白项自变量空白项 [',' 空白项自变量空白项]] ')' 空白项 '=' 空白项函数表达式
自定义函数调用 → 自定义函数名空白项 '(' 空白项因子空白项 [',' 空白项因子空白项 [',' 空白项因子空白项]] ')'
自定义函数名 → 'f' | 'g' | 'h'
函数表达式 → 表达式 (注：本次作业中函数表达式保证不会调用自己或其他自定义函数)
2.2 程序结构

这次作业为解决三角函数和函数调用问题，新增了两个类:

Function: 用于装载自定义函数，将函数表达式和函数形参建立联系。

Circular: 三角函数类，实现了Factor接口。具体属性如下:

  private final String base;//用于辨认sin和cos
  private final Expr expr;//记录三角函数中因子
  private BigInteger exp;//记录指数

2.3 设计思路

本次采用字符串替换解决自定义函数问题，具体实现是设置一个Function类，Function类属性为:
```
 private char sign;//记录函数名(f|g|h)
 private String expr;//记录函数表达式
```
在读入函数定义时，将表达式中的形参依次替换为u、v、w，并储存在一个Function中的expr里。在函数调用时，再将u、v、w依次替换为因子。比如:

读入函数f(x,z,y) = x+y+z，储存为f(u,v,w) = u+w+v

调用f(sin(x),z,y)，整体替换为sin(x)+y+z
对于三角函数，我新设了一个Circular类，具体定义在程序结构已经解释。而在处理三角函数一个重要的问题是如何判断两个三角函数中的表达式是否相等，为了处理这个问题，我选择在递归下降途中进行加减法化简，保证三角函数中的表达式形式唯一，正常遍历比较即可判断两个三角函数中的表达式是否相等。具体实现是在Expr中设置了一个新的属性:
```
private ArrayList<Calc> newterms;
```
在parseExpr()得到一个新的Expr时，先将这个表达式格式化为Calc形式，再根据newterms进行加减法化简，实现表达式唯一性。

2.4 分析评估

2.4.1 度量分析

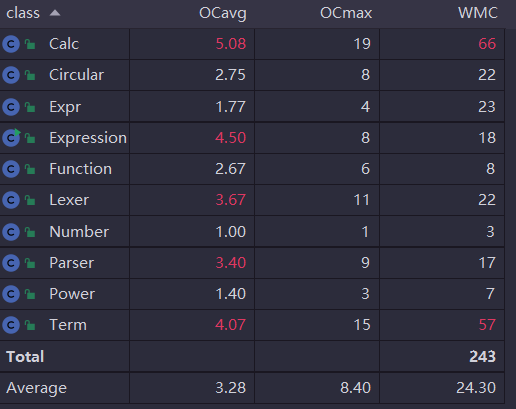
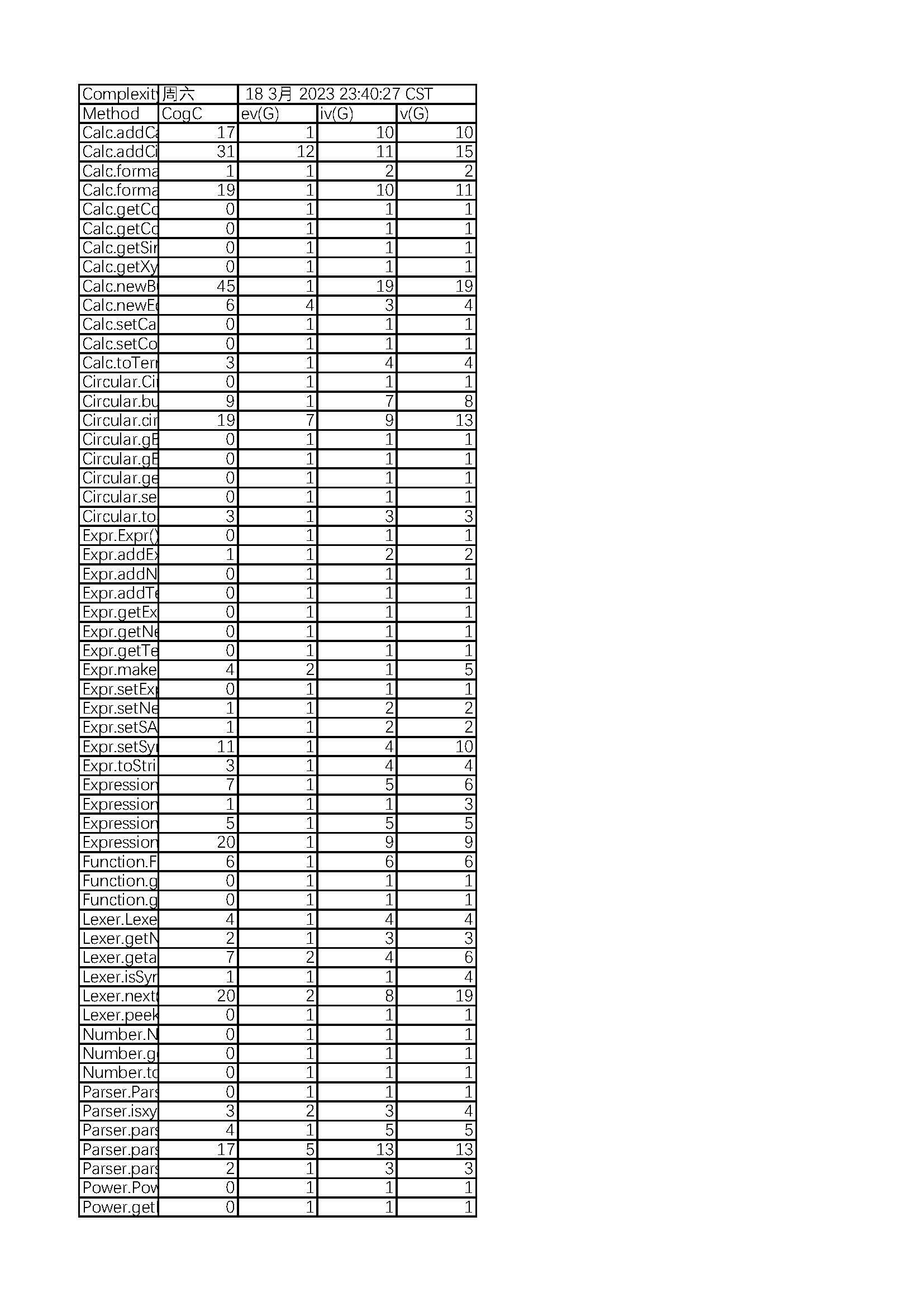
由于需要分析的语法增加，Parser和Lexer的复杂度不可避免地增加，但Term和Calc的复杂度过大是由于我将加减法和乘法加入该类中，并未把他抽象为一个新的工具类。而且因为我并未实现表达式的排序和哈希值编写，所以我所有设计表达式的比较都是使用了双层循环，这导致了我所有涉及比较的函数复杂度极高。

2.4.2 架构分析

我认为本次作业的我的架构极为糟糕，巨型类和方法较多，许多行为并未抽象成新的类。类于类之间的耦合度过高，许多方法的条件分支过多，导致我在代码维护和检测时都遇到了极大的困难。

2.4.3 bug分析

本次作业我在课下所做的检测工作虽然更加认真，但由于架构过于糟糕，我在强测和互测至少发现了6个大大小小的bug，基本上每一个巨型方法内都会有一个bug。这些bug包括输出时sin(0)**0输出错误，浅克隆，函数调用时出现空白字符会死循环等。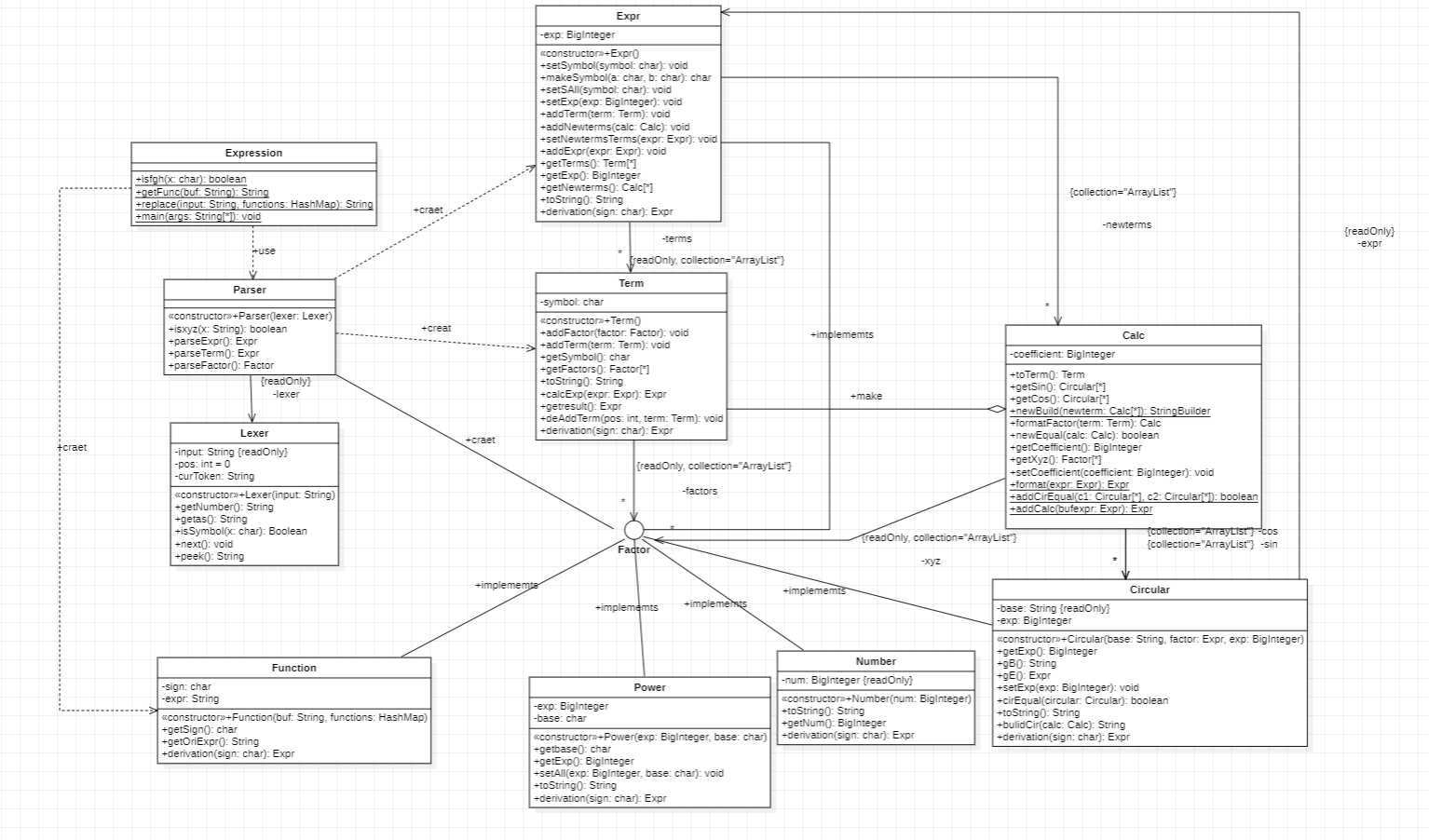
本次作业的互测时我也发现了许多同房的人的bug，这些bug主要集中于

函数嵌套
加减法化简
函数调用时使用复杂因子
边界数据的输出
三、第三次作业

3.1 作业内容
本次作业新增内容较少，只有求导因子求导和函数定义时调用，下面时求导因子的形式化表达:
求导因子 → 求导算子空白项 '(' 空白项表达式空白项 ')'
求导算子 → 'dx' ｜'dy' ｜'dz'
3.2 程序结构

本次作业增加类容较少，程序结构并未发生过多的改变，主要是实现新的函数。

3.3 设计思路

本次作业涉及函数定义时调用函数和函数定义时求导，因此我在储存函数前对函数表达式进行递归下降解析，在将解析得到的Expr转化为字符串储存在Function中，之后的流程与第二次作业几乎相同。
对于求导问题，我采用多态解决，在接口Factor中定义求导方法derivation，在Factor的各个不同实现中重写不同的求导规则，最后直接对求导因子中的表达式调用方法即可得到结果。下面是各个类的求导方法:

Expr: 由于在求导因子的表达式解析中一定化简了乘法，所以Expr的指数一定为1，只需要对Expr中的每一个Term调用求导方法，返回值为表达式。

Term: 对Term使用乘法法则，即遍历所有因子，每次循环时，对当前因子求导，保留其他因子，伪代码如下:

public Expr derivation(){
Expr expr = new Expr();
for(Factor factor : this.getFactors){
  Term term = new Term();
  term.addTerm(otherFactors);
  term.addFactor(factor.derivation());
  //处理符号函数(有一定篇幅，此处省略)
  expr.addTerm(term);
}
return expr;
}

Number:常数因子的求导为0。
Power:幂函数求导只需要将整体乘以指数，再将指数减一即可。

Circular:三角函数的求导较为复杂，需要考虑指数，链式求导，函数名变化，伪代码如下:

public Expr derivation() {
      Expr expr = new Expr();
      Term term = new Term();
      String base = (this.base.equals("sin")) ? "cos" : "sin";//处理函数名
      term.addFactor(new Number(this.exp));//最外层的幂函数求导
      term.addFactor(new Circular(this.base, this.expr, this.exp.subtract(BigInteger.ONE)));//最外层的幂函数求导
      term.addFactor(new Circular(base, this.expr, BigInteger.ONE));//三角函数求导
      term.addFactor(this.expr.derivation());//对三角函数内表达式求导
      //处理符号函数(有一定篇幅，此处省略)
      expr.addExpr(bufexpr);
      return expr;
  }

3.4 分析评估

3.4.1 度量分析

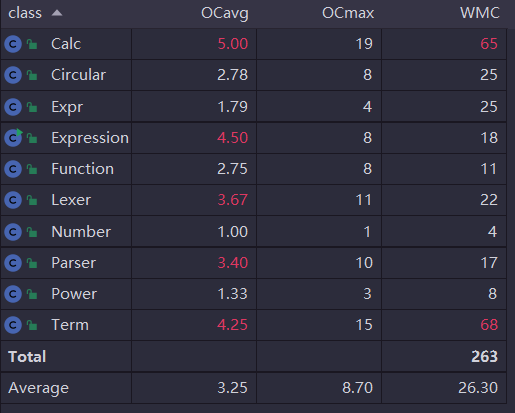
本次因为作业类容简单，我没有进行重构，所有不论是代码规模，类复杂度还是方法复杂度都雪上加霜，特别是对函数表达式还要进一步解析，导致主函数和Function类的复杂度极高

3.4.2 架构分析

因为为进行重构，我程序的架构整体上还是挺糟糕的，但对于求导因子解析的架构我自认为还是比较清晰的。对于每一个类都统一接口，重写求导方法，使程序处理求导时调用方法形式较为统一。

3.4.3 bug分析

在本次作业，自己的程序和同房的程序都没有发现什么bug，比较常见的还是对函数定义采取字符串处理而导致的卡性能型bug。

四、互测策略

使用测评机大规模测试
构造边界数据，如超过int范围的大数，0次幂等
利用指导书中的一些细节说明，如构造多符号的因子、项，前导0，空格等
针对一些复杂的函数和类构造数据，如针对实现三角函数化简的函数构造数据
~~翻阅水群，抄抄大佬的数据~~

五、架构设计体验&心得体会

在经历第一单元的作业后，我觉得动笔写代码前的架构设计还是值得花费大量时间去思考的，第一次作业写作前，只思考了递归下降的架构，剩下的乘法和加减法并未深思，导致这方面的架构问题重重，巨型方法扎堆，甚至写进了主函数，测试结构也反映了bug多数都是藏在这些不完善的架构中。的二次作业倒是对第一次作业进行了部分重构，将加法整理进Calc类，乘法整理进Term类，但仍然没有对本单元新增的任务进行结构分析，导致错误频出。第三次作业倒是依靠第二次作业时激烈的互测幸免于难，侥幸无伤过关，但架构问题还是值得我在下次作业时认真思考的。

同时我认为java的知识储备还需增强，因为不熟悉HashMap和TreeMap的使用，我第一单元走了很多弯路，并遇到了极难化简、比较和查找的问题。为此，我应该夯实基础，不断弥补自身的不足，写出更加完善的项目。

...全文