最短路简介（Floyd、Bellman_Ford、SPFA、Dijkstra）

[illjlack]

 

在图论中最短路径是两个节点之间经过的边权值之和最小的路径，是一种在图上的搜索，满足最优子结构（可以使用动态规划和贪心算法）

最优子结构:最短路径的子路径也是最短路径(有可以到达的负环的图不满足最优子结构)

单源最短路问题

找到从给定源节点到其它节点的最短路径

相关算法

Floyd

动态规划的思想，是多源的（算出了每两个节点的最短距离），复杂度O(n^3)

用f[k][x][y]表示中间只经过1~k的点的最短路，转移为：f[k][x][y]=min(f[k-1][x][y]/*x->y不经过k点的情况*/,f[k-1][x][k]+f[k-1][k][y]/*x->y经过k点情况*/)

第k层依赖k-1层，每一层x,y都要遍历完，自底向上动态规划,复杂度O(n^3)

Bellman_Ford

动态规划的思想，是单源的，复杂度O(nm)

Bellman-Ford 算法的基本思想是对所有边进行松弛操作，每次松弛操作都会更新一些最短路径的估计值。算法进行 n-1 轮松弛操作，其中 n 是图中顶点的数量。在每一轮松弛操作中，算法都会遍历图中的所有边，对每一条边进行松弛操作。

可以这么想：f[k][x]表示从起点到x最多经过k条边的最短路

转移为：

第k层依赖k-1层，每一层要遍历完所有边（没有入度的边也要更新），自底向上动态规划,复杂度O(nm)

//Floyd、Bellman_Ford实际用的时候，不用分层，分层隔绝了每层先更新部分对后更新的依赖的影响，这里的影响是好的所以不用分层

SPFA（Shortest Path Faster Algorithm）

bellman_ford的队列优化，它利用了这样一个事实：在进行松弛操作时，只有那些在上一轮松弛操作中发生变化的顶点才可能对其他顶点产生影响。

基于这个观察，SPFA 算法使用一个队列来维护所有可能对其他顶点产生影响的顶点。

SPFA 算法的时间复杂度取决于具体的图结构和边权分布。在最坏情况下，它的时间复杂度与 Bellman-Ford 算法相同，为 O(nm)，但在实际应用中，SPFA 算法通常比 Bellman-Ford 算法快很多。

Dijkstra

贪心思想，是单源最短路径问题的。它不能处理带有负权边的图。

每次选择距离源点最近的未确定顶点，然后更新与其相邻顶点的最短路径长度。

复杂度O(n^2+m),其中一个n是n次贪心，另一个n是找最近点，m是所有边会遍历一遍。

找点可以维护一个优先队列等操作优化，比Bellman_Ford快。

因为贪心算法只看下一步，所以它不能处理带有负权边的图。比如下图：它会按序号更新，不会更新已经遍历的点，下面的情况就出错了

 

 

拓展（思考）

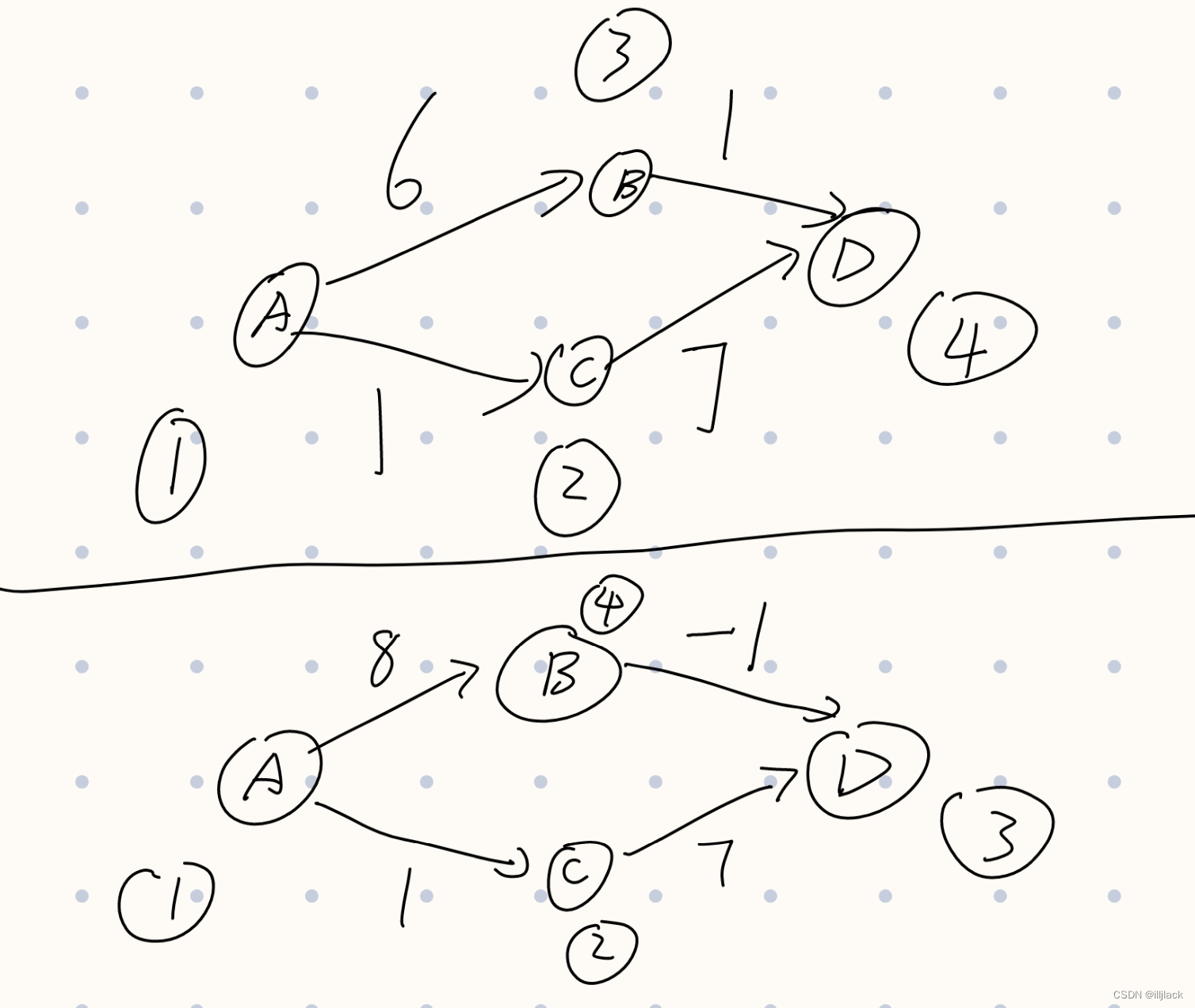
• 对于动态规划，重要的是能设计出dp的顺序

• 一般图的最长路因为没有最优子结构所以是NP问题，只能硬搜

• DAG(有向无环图)上，最短、最长路都满足最优子结构，所以能用dp,先拓扑排序，按dp顺序转移

[给小猫咪顺毛]

太帅辣