蓝桥练习05-找素数

代码骑士

优质创作者: 游戏开发技术领域

2023-04-07 16:06:25

洛谷-P3912 素数个数

题目描述

求1,2,⋯,N 中素数的个数。

输入格式

一行一个整数 N。

输出格式

一行一个整数，表示素数的个数。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

对于 40%40% 的数据，1≤N≤1061≤N≤106。

对于 80%80% 的数据，1≤N≤1071≤N≤107。

对于 100%100% 的数据，1≤N≤1081≤N≤108。

算法1：

思路：暴力算法，枚举0~N的整数，对每个整数从2~n-1进行判断是否能被除了1和本身外的数整除，如果能则不是素数，反之，是素数。

#include<bits/stdc++.h>
using namespace std;

void getPrime1(int N){
	int count=0;
	for(int i=2;i<N;i++){//2~N之间的素数 
		int f=1;//默认是素数 
		for(int j=2;j<i;j++){
			if(i%j==0){
				f=0;//不是素数
				break; 
			}
		} 
		if(f) count++;
	}
	cout<<count;
}
int main(){
	int n;
	cin>>n;
	getPrime1(n);
	return 0;
}

思想非常简单，代码也好理解，但是只能通过两个测试点，其余的都超时了。

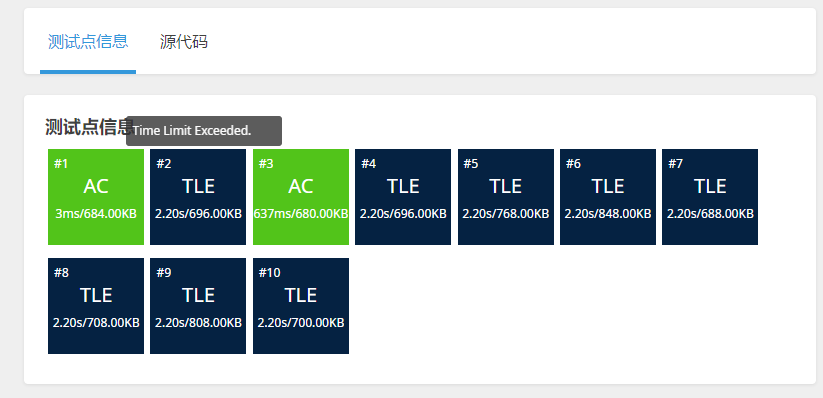
算法 2 ：使用开方的办法，减少循环次数。

#include<bits/stdc++.h>
using namespace std;
void getPrime2(int N){
	int count=0;
	for(int i=2;i<=N;i++){
		bool f=true;//默认是素数 
		for(int j=2;j<=sqrt(i);j++){
			if(i%j==0){
				f=false;//不是素数 
				break; 
			}		
		}
		if(f){
			//cout<<i<<",";
			count++;
		}
	}
	cout<<count<<endl;
}

int main(){
    int n;
    cin>>n;
	getPrime2(n);
	return 0;
}

这回通过的测试点比上个多出3个，效果还不错，但其余的测试还是没有通过，超时了。

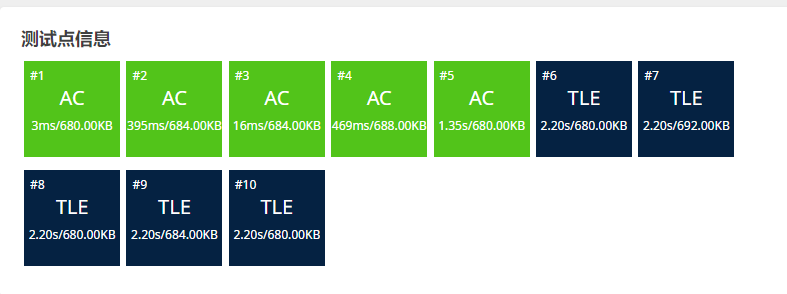
算法3：使用-埃氏素数筛法

思路：

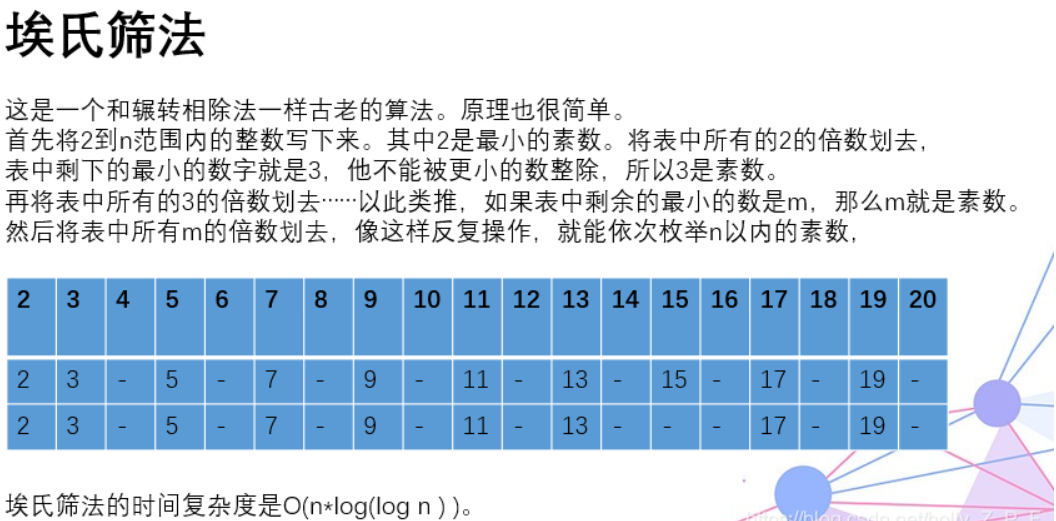
参考原文：https://blog.csdn.net/holly_Z_P_F/article/details/85063174?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522168085181016800227433258%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=168085181016800227433258&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-85063174-null-null.142^v82^insert_down38,201^v4^add_ask,239^v2^insert_chatgpt&utm_term=%E5%9F%83%E6%B0%8F%E7%AD%9B&spm=1018.2226.3001.4187

代码：

#include<bits/stdc++.h>
using namespace std;
void getPrime3(int N){
	int count=0; //统计素数个数 
	const int maxn=10000;//数组最大值 
	bool isprime[maxn];
	//初始化
	for(int i=0;i<=N;i++){
		isprime[i]=true;//默认0~N全是素数 
	} 
	
	isprime[0]=isprime[1]=false;//0和1不是素数，最小的素数是2
	
	for(int i=2;i<=N;i++){//从2往后筛 
		if(isprime[i]){
			for(int j=2*i;j<=N;j+=i){
				isprime[j]=false;//将素数的倍数全部筛除 
			} 
		} 
	} 
	for(int i=0;i<=N;i++){
		if(isprime[i]){//最后剩下的全是素数 
			count++;
		}
	} 
	cout<<count;
}

int main(){
    int n;
    cin>>n;
	getPrime3(n);
	return 0;
}

我第一次写完发现循环次数比第一个算法还多，通过的测试点更少了，还不如开平方。

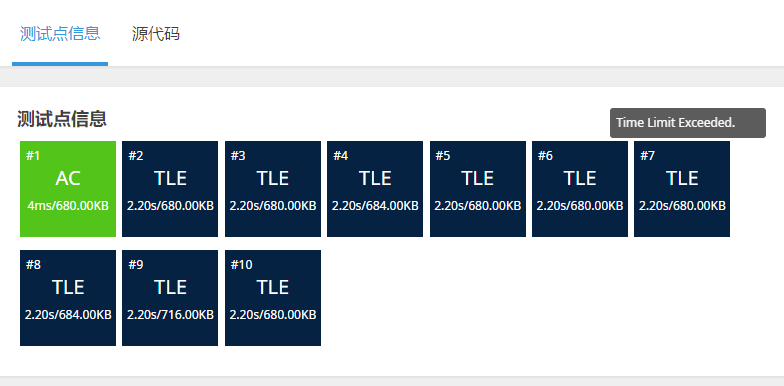
看了一下大佬的优化算法，发现是自己的数组范围开太小了，扩大之后：

#include<bits/stdc++.h>
using namespace std;
void getPrime3(int N){
	int count=0; //统计素数个数 
	const int maxn=100000005;//数组最大值 
	bool isprime[maxn];
	for(int i=0;i<=N;i++)	isprime[i]=true;//默认0~N全是素数 
	isprime[0]=isprime[1]=false;//0和1不是素数，最小的素数是2
	for(int i=2;i<=N;i++){//从2往后筛 
		if(isprime[i]){
			for(int j=2*i;j<=N;j+=i){
				isprime[j]=false;//将素数的倍数全部筛除 
			} 
			if(isprime[i]) ++count;
		} 
	} 

	cout<<count; 
}

int main(){
    int n;
    cin>>n;
	getPrime3(n);
	return 0;
}

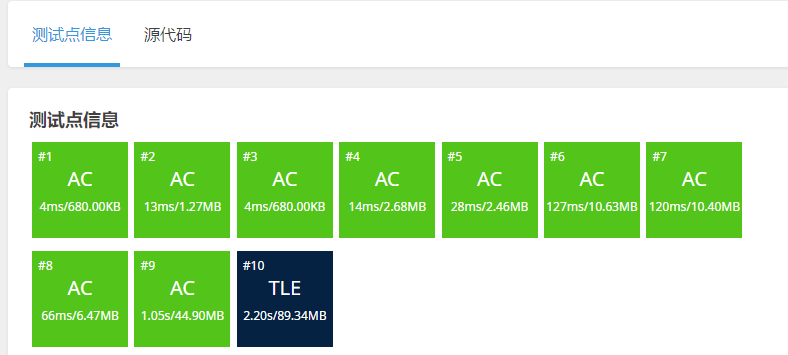
再次优化

https://blog.csdn.net/qq_62986243/article/details/123761297?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522168085181016800227433258%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=168085181016800227433258&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-2-123761297-null-null.142^v82^insert_down38,201^v4^add_ask,239^v2^insert_chatgpt&utm_term=%E5%9F%83%E6%B0%8F%E7%AD%9B&spm=1018.2226.3001.4187

#include<iostream>
using namespace std;
bool a[100000005];
int main()
{
	int n,i,cnt=0;
	cin>>n;
	for(int i=2;i*i<=n;++i){//其他博客写的是for(i=0;i<n;++i),这里可以改成这样，因为在前面已经筛过了
		if(a[i]==0){
			for(int j=i*i;j<=n;j+=i){//这里直接j=i*i,而不用j=i*2;因为前面有2*i,3*i,4*i....,(i-1)*i
				a[j]=1;
			}
		}
	}
	for(i=2;i<=n;++i){
		if(a[i]==0)++cnt;
	}
	cout<<cnt;
	return 0;
}

还是差一个测试点，但是已经很简洁了，优化果然牛。

还有一个线性筛留着下次学吧。

...全文