matlab_信号采样与重构

[鹅毛在路上了]

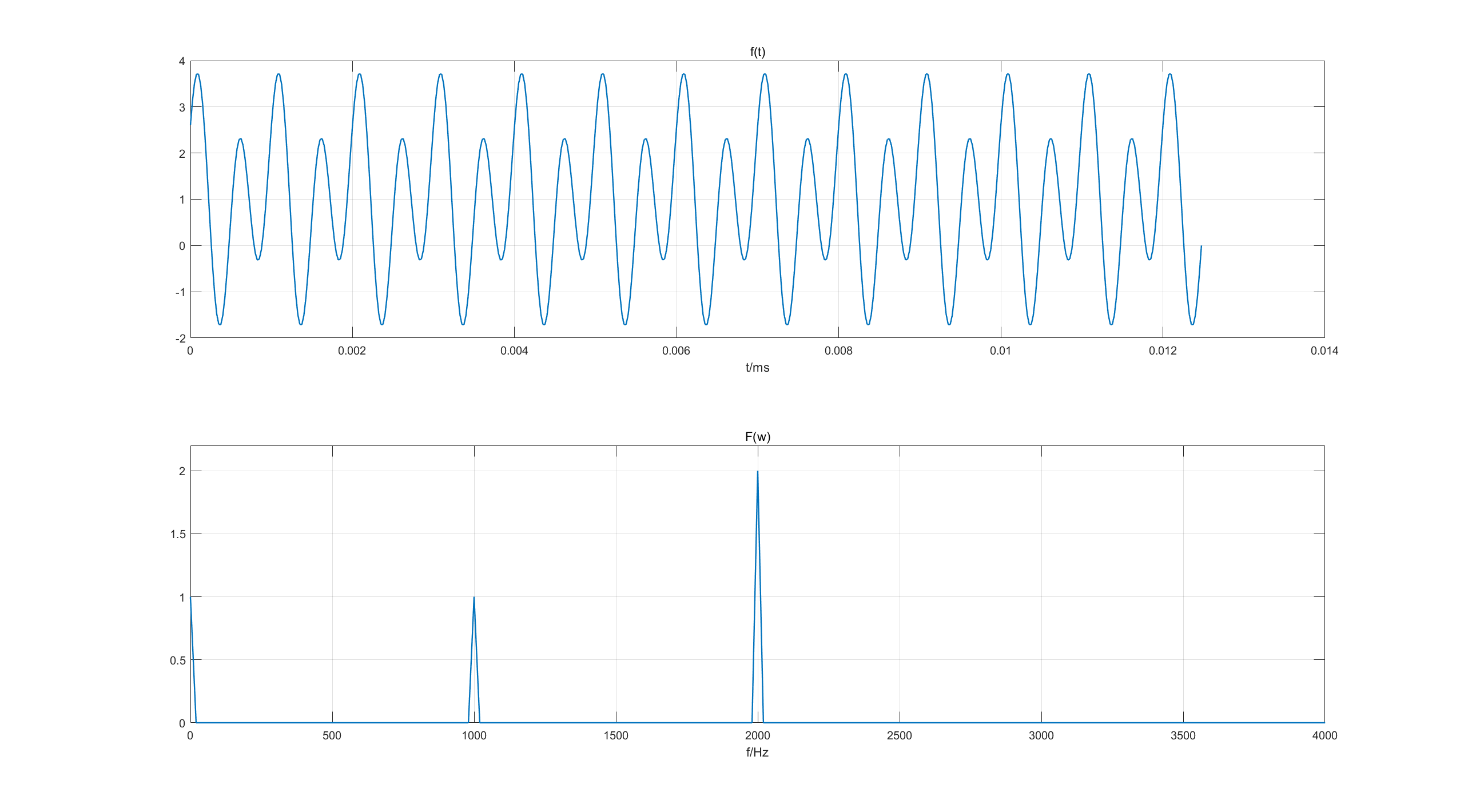
用Matlab画出f(t)=1+cos(2000πt)+2sin(4000πt)经过最小抽样频率抽样后的序列及其幅频特性曲线，并由抽样序列恢复出连续时间信号，并画出其时域波形，对比与原始信号的时域波形有何区别?

最低采样频率即奈奎斯特采样频率，至少为最高频率2000Hz的2倍，但是实际上由4000Hz抽样后得出来的频谱中并不能明显看出2000Hz得成分，4010~4400Hz逐渐明显；

信号重构原理：
先定义一个长度为t的零向量reconstructed_f，用于存储插值重建后的信号。然后，使用一个循环来遍历所有的采样点，并使用sinc函数进行插值计算，即可得到完整的插值重建后的信号。

示例代码：

clc,clear,close all;
% 生成信号f(t)
t = 0:0.00001:0.02;
f = 1 + cos(2000*pi*t) + 2*sin(4000*pi*t);

% 对信号f(t)进行采样
Fs = 4000; % 采样频率
Ts = 1/Fs; % 采样周期
n = 0:Ts:0.02;
sampled_f = 1+cos(2000*pi*n)+2*sin(4000*pi*n);

% 绘制采样后的序列及其幅频特性曲线
subplot(2,1,1)
stem(n,sampled_f)
xlabel('Time (s)')
ylabel('Amplitude')
title('Sampled Sequence')

N = length(sampled_f);
freq = linspace(-Fs/2,Fs/2,N);
Y = fftshift(abs(fft(sampled_f))/N);
subplot(2,1,2)
plot(freq,Y)
xlabel('Frequency (Hz)')
ylabel('Magnitude')
title('Frequency Response of Sampled Sequence')

% 插值重建信号f(t)
reconstructed_f = zeros(1,length(t));
for i = 1:length(n)
    reconstructed_f = reconstructed_f + sampled_f(i)*sinc((t-(i-1)*Ts)/Ts);
end

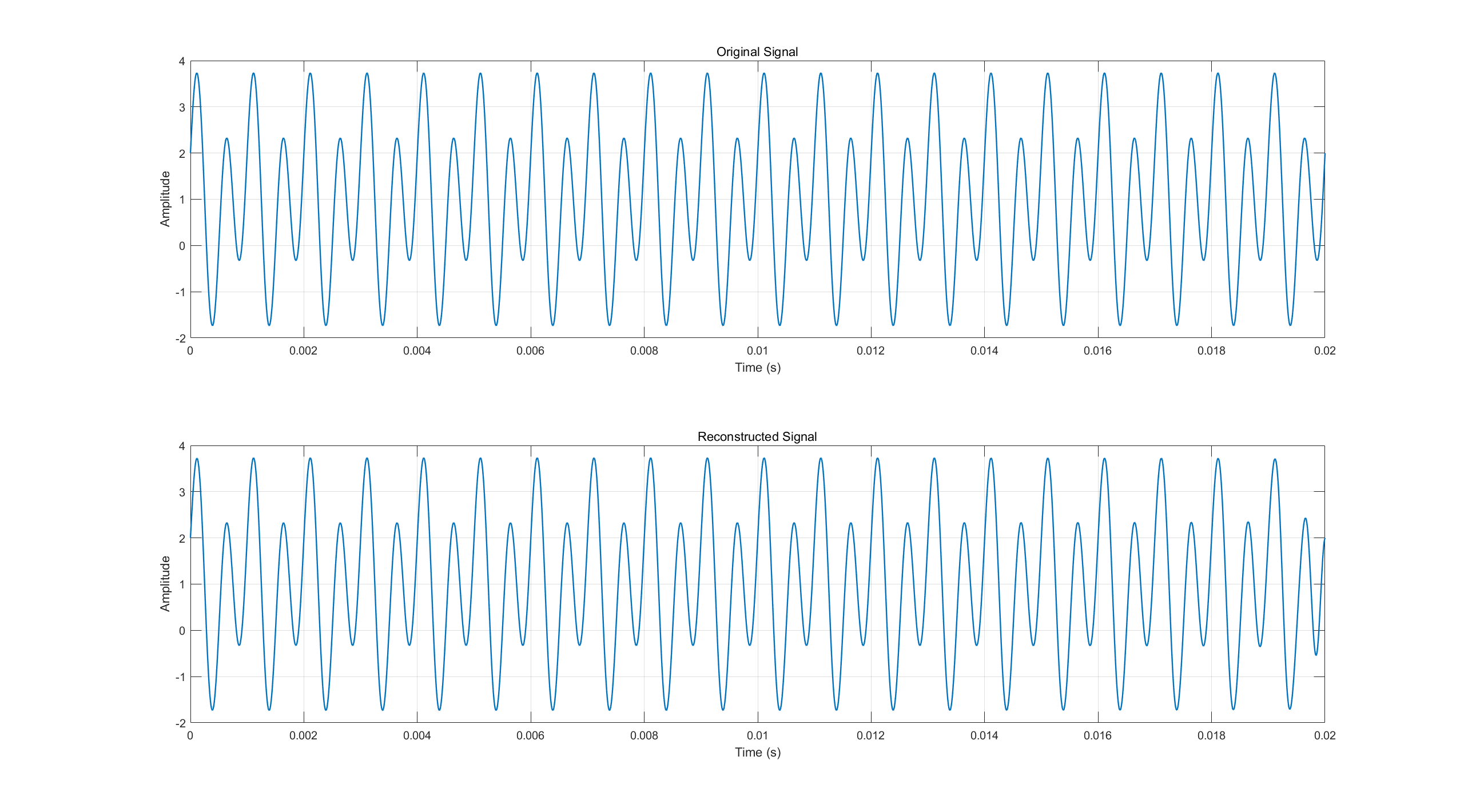
% 绘制恢复后的信号时域波形
figure
subplot(2,1,1)
plot(t,f)
xlabel('Time (s)')
ylabel('Amplitude')
title('Original Signal')

subplot(2,1,2)
plot(t,reconstructed_f)
xlabel('Time (s)')
ylabel('Amplitude')
title('Reconstructed Signal')

最终实验效果：