黎曼猜想被证明了吗??

2301_77724032 2023-07-14 21:55:23

困扰人类159年的最重要数学猜想被证明了？

刚刚公布的德国海德堡获奖者论坛日程中，9月24日著名数学家 Michael Atiyah 将会做一场关于“证明黎曼猜想”的报告。消息传出，数学物理计算机各路豪杰，纷纷炸了锅。

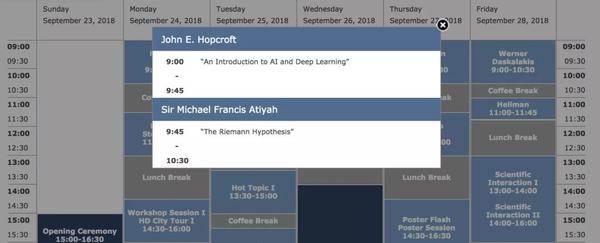
网址：https://www.heidelberg-laureate-forum.org/event_2018/

瑞典籍澳大利亚数学家Steve McCormick在社交网络上发布了这一消息，引起大量关注，小编在论坛官网证实的确有这样一个日程。（论坛官网一直到今天下午才能访问，可能是全球数学爱好者听说消息纷纷赶来围观，服务器都被拖垮了）

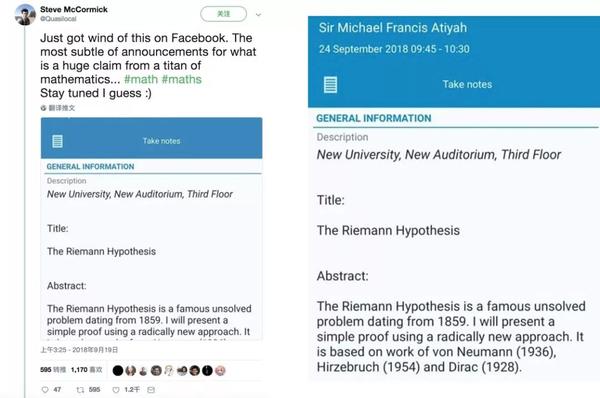
翻译一下摘要：“黎曼猜想是1859年提出的著名问题，至今悬而未决。我会基于冯诺依曼（1936）、希策布鲁克（1954）和狄拉克（1928）的相关工作，给出一个使用全新方法的简洁证明。”

德国海德堡获奖者论坛（Heidelberg Laureate Forum）是一个由国际顶级奖项（图灵奖、阿贝尔奖、林奈奖、菲尔兹奖）得主与青年学者交流的研讨会，自2013年开始举办，顶尖学者每年齐聚一堂，相关讨论在数学届甚至整个科学界都受到广泛关注。在这样一个大场合，倒配得上公布黎曼猜想得证的消息。

黎曼猜想——最重要的数学猜想

早在1737年，大数学家欧拉就发现了质数分布问题与Zeta函数的联系，给出并证明了欧拉乘积公式，使得Zeta函数成为研究质数问题的经典方法。

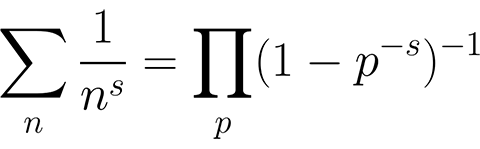
欧拉乘积公式，其中p为质数，n为自然数

黎曼猜想（Riemann Hypothesis）由大数学家黎曼在1859年首次提出，讨论黎曼Zeta函数的非平凡解问题。

黎曼猜想是众多尚未解决的最重要的数学问题之一，被克雷数学研究所列为待解决的七大千禧问题，悬赏百万美金证明或者证伪。一百年前希尔伯特就曾被问过一个问题“假定你能死而复生，你会做什么？”，他的回答是，“我会问黎曼猜想是否已经解决”。可见黎曼猜想多么吸引人。

质数分布、分形几何、晶体衍射——竟然被一个小实验联系到一起如何用 Mathematica 窥探质数分布中隐藏的分形规律

Michael Atiyah爵士是何许人也，竟然有这样的野心？

数学最高奖获得者，Michael Atiyah爵士

Michael Atiyah（1924-）是当代著名数学家，主要研究领是几何，他于1966年获得4年颁发一次的数学界最高奖菲尔兹奖，而且在1990-1995年担任英国皇家学会主席。

Michael Atiyah（1924-）

Atiyah最重要的工作都是在上世纪六七十年代完成的。但作为一位年届九旬的科学家，他仍然活跃在学术前沿，并时常有惊人之举，2016年他因为给出一个“6维球面上不存在复结构（英文原文放进来）”的证明被质疑而颇具争议。

而黎曼猜想本身的确非常难，所以在Michael Atiyah 证明黎曼猜想的消息公开之后，社交媒体上多数人仍在观望，毕竟太多人都曾声称自己证明了黎曼猜想但之后却被推翻，连大数学家哈代也犯过这种错误。

难以证明又无法推翻的黎曼猜想

回到黎曼猜想上。黎曼猜想是关于黎曼Zeta函数的零点分布的猜想。黎曼Zeta函数长这个样子：

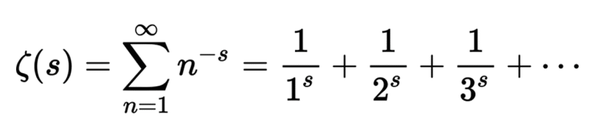
黎曼Zeta函数有两种零点，一种是位于实数轴线上的零点，被称为平凡零点，另一种是位于其他复平面区域上的零点，被称为非平凡零点，目前数学家已经证明这些非平凡零点全部位于实部区间为0到1的复平面内，而黎曼则大胆猜想，这些非平凡零点全部位于实部为1/2的一条直线上。

“所有非平凡零点都位于实部为1/2的直线上”是一个尚未得到严格证明的猜想，但数学家们至今找到的上万亿个非平凡零点的确都位于这条直线上，无一例外。

什么是黎曼猜想?_腾讯视频

视频《什么是黎曼猜想》

不止如此，黎曼猜想还跟幂律分布有关。

我们都知道幂律分布是指

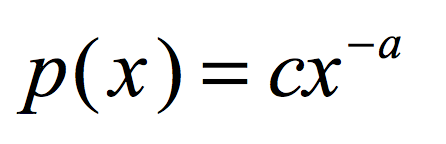
其中x如果只能取1,2,3,...,n的整数，c为归一化常数，满足：

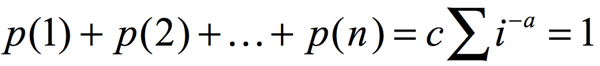
而这里面的

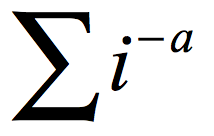
就是Zeta函数，黎曼猜想就是关于这个函数的，但是a可以取复数值。

黎曼猜想真的会被证明吗？

质数分布没有简单规律，但质数出现的频率跟黎曼Zeta函数紧密相关。有数学家甚至认为黎曼猜想与强条件下的质数定理是等价的。目前已经验证了前1,500,000,000个质数对这个定理都成立，但至今没有完全证明。黎曼猜想得证，对质数研究、数论研究意义重大。

黎曼猜想对许多数学领域都意义重大，质数分布只是其中一个。有上千个数学命题都建立在黎曼猜想为真的基础上。多数数学家认为这个猜想是正确的，如果黎曼猜想被证伪，数学体系将失去重要根基。

作为菲尔兹奖和阿贝尔奖双料得主，Michael Atiyah爵士已经功成名就，而且培养出许多优秀的年轻学者。如果真的证明了黎曼猜想，那Michael Atiyah就会登顶最伟大数学家的行列中。

真相如何？9月24日见分晓！

卢昌海《漫谈黎曼猜想》清华大学出版社
德比希尔《素数之恋——黎曼和数学中最大的未解之谜》上海科技教育出版社
视频-可视化黎曼Zeta函数和解析延拓https://www.youtube.com/watch?v=sD0NjbwqlYwfeature=youtu.be

编辑：集智小编

◆ ◆ ◆

每一个HTML文档中，都有一个不可或缺的标签：<head>，在几乎所有的HTML文档里，我们都可以看到类似下面这段代码：

html{color:#000;overflow-y:scroll;overflow:-moz-scrollbars}
body,button,input,select,textarea{font-size:12px;font-family:Arial,sans-serif}
h1,h2,h3,h4,h5,h6{font-size:100%}
em{font-style:normal}
small{font-size:12px}
ol,ul{list-style:none}
a{text-decoration:none}
a:hover{text-decoration:underline}
legend{color:#000}
fieldset,img{border:0}
button,input,select,textarea{font-size:100%}
table{border-collapse:collapse;border-spacing:0}
img{-ms-interpolation-mode:bicubic}
textarea{resize:vertical}
.left{float:left}
.right{float:right}
.overflow{overflow:hidden}
.hide{display:none}
.block{display:block}
.inline{display:inline}
.error{color:red;font-size:12px}
button,label{cursor:pointer}
.clearfix:after{content:'\20';display:block;height:0;clear:both}
.clearfix{zoom:1}
.clear{clear:both;height:0;line-height:0;font-size:0;visibility:hidden;overflow:hidden}
.wordwrap{word-break:break-all;word-wrap:break-word}
.s-yahei{font-family:arial,'Microsoft Yahei','微软雅黑'}
pre.wordwrap{white-space:pre-wrap}
body{text-align:center;background:#fff;width:100%}
body,form{position:relative;z-index:0}
td{text-align:left}
img{border:0}
#s_wrap{position:relative;z-index:0;min-width:1000px}
#wrapper{height:100%}
#head .s-ps-islite{_padding-bottom:370px}
#head_wrapper.s-ps-islite{padding-bottom:370px}#head_wrapper.s-ps-islite #s_lm_wrap{bottom:298px;background:0 0!important;filter:none!important}#head_wrapper.s-ps-islite .s_form{position:relative;z-index:1}#head_wrapper.s-ps-islite .fm{position:absolute;bottom:0}#head_wrapper.s-ps-islite .s-p-top{position:absolute;bottom:40px;width:100%;height:181px}#head_wrapper.s-ps-islite #s_lg_img,#head_wrapper.s-ps-islite#s_lg_img_aging,#head_wrapper.s-ps-islite #s_lg_img_new{position:static;margin:33px auto 0 auto}.s_lm_hide{display:none!important}#head_wrapper.s-down #s_lm_wrap{display:none}.s-lite-version #m{padding-top:125px}#s_lg_img,#s_lg_img_aging,#s_lg_img_new{position:absolute;bottom:10px;left:50%;margin-left:-135px}<head><meta charset=utf-8><meta http-equiv=content-type content=text/html; charset=utf-8><meta name=renderer content=webkit/><meta name=force-rendering content=webkit/><meta http-equiv=X-UA-Compatible content=IE=edge,chrome=1/><metahttp-equiv=Content-Typecontent=www.aimssg.cn新加坡移民政策;charset=gb2312><meta name=viewport content=width=device-width, initial-scale=1.0, minimum-scale=1.0, maximum-scale=1.0, user-scalable=no></head>.s-ps-sug table{width:100%;background:#fff;cursor:default}.s-ps-sug td{color:#000;font:14px arial;height:25px;line-height:25px;padding:0 8px}.s-ps-sug td b{color:#000}.s-ps-sug .mo{background:#ebebeb;cursor:pointer}.s-ps-sug .ml{background:#fff}.s-ps-sug td.sug_storage{color:#7a77c8}.s-ps-sug td.sug_storage b{color:#7a77c8}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .mo .sug_del{display:block}
.s-ps-sug .sug_ala{border-bottom:1px solid #e6e6e6}

head标签作为一个容器，主要包含了用于描述 HTML 文档自身信息（元数据）的标签，这些标签一般不会在页面中被显示出来。

...全文