1,345
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享这篇文章最初发表在 NVIDIA 技术博客上。有关此类的更多内容,请参阅最新的 数据科学 新闻和教程。
线性回归是最简单的机器学习模型之一。它通常不仅是学习数据科学的起点,也是构建快速简单的最小可行产品( MVP )的起点,然后作为更复杂算法的基准。
一般来说,线性回归拟合最能描述特征和目标值之间线性关系的直线(二维)或超平面(三维及三维以上)。该算法还假设特征的概率分布表现良好;例如,它们遵循高斯分布。
异常值是位于预期分布之外的值。它们导致特征的分布表现较差。因此,模型可能会向异常值倾斜,正如我已经建立的那样,这些异常值远离观测的中心质量。自然,这会导致线性回归发现更差和更有偏差的拟合,预测性能较差。
重要的是要记住,异常值可以在特征和目标变量中找到,所有场景都可能恶化模型的性能。
有许多可能的方法来处理异常值:从观察值中删除异常值,处理异常值(例如,将极端观察值限制在合理值),或使用非常适合自己处理此类值的算法。本文重点介绍了这些稳健的方法。
我使用相当标准的库:numpy、pandas、scikit-learn。我在这里使用的所有模型都是从scikit-learn的linear_model模块导入的。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn import datasets from sklearn.linear_model import (LinearRegression, HuberRegressor, RANSACRegressor, TheilSenRegressor)
鉴于目标是展示不同的鲁棒算法如何处理异常值,第一步是创建定制的数据集,以清楚地显示行为中的差异。为此,请使用scikit-learn中提供的功能。
首先创建一个包含 500 个观察值的数据集,其中包含一个信息性特征。只有一个特征和目标,绘制数据以及模型的拟合。此外,指定噪声(应用于输出的标准差),并创建包含基础线性模型系数的列表;也就是说,如果线性回归模型适合生成的数据,系数会是多少。在本例中,系数的值为 64.6 。提取所有模型的系数,并使用它们来比较它们与数据的拟合程度。
接下来,用异常值替换前 25 个观察值(占观察值的 5% ),远远超出生成的观察值的质量。请记住,先前存储的系数来自没有异常值的数据。包括他们会有所不同。
N_SAMPLES = 500 N_OUTLIERS = 25 X, y, coef = datasets.make_regression( n_samples=N_SAMPLES, n_features=1, n_informative=1, noise=20, coef=True, random_state=42 ) coef_list = [["original_coef", float(coef)]] # add outliers np.random.seed(42) X[:N_OUTLIERS] = 10 + 0.75 * np.random.normal(size=(N_OUTLIERS, 1)) y[:N_OUTLIERS] = -15 + 20 * np.random.normal(size=N_OUTLIERS) plt.scatter(X, y);
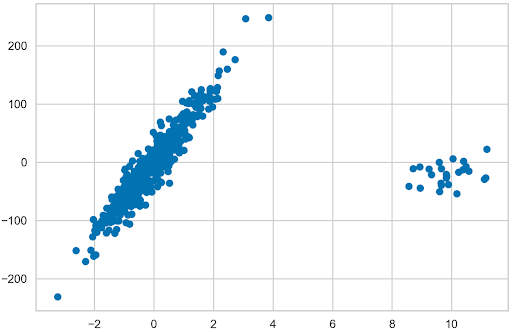 图 1 。生成的数据和手动添加的异常值
图 1 。生成的数据和手动添加的异常值
从良好的旧线性回归模型开始,该模型可能受到异常值的高度影响。使用以下示例将模型与数据拟合:
lr = LinearRegression().fit(X, y) coef_list.append(["linear_regression", lr.coef_[0]])
然后准备一个用于绘制模型拟合的对象。plotline_X对象是一个 2D 数组,包含在生成的数据集指定的间隔内均匀分布的值。使用此对象获取模型的拟合值。它必须是 2D 数组,因为它是scikit-learn中模型的预期输入。然后创建一个fit_df数据框,在其中存储拟合值,通过将模型拟合到均匀分布的值来创建。
plotline_X = np.arange(X.min(), X.max()).reshape(-1, 1) fit_df = pd.DataFrame( index = plotline_X.flatten(), data={"linear_regression": lr.predict(plotline_X)} )
准备好数据框架后,绘制线性回归模型与具有异常值的数据的拟合图。
fix, ax = plt.subplots() fit_df.plot(ax=ax) plt.scatter(X, y, c="k") plt.title("Linear regression on data with outliers");
图 2 显示了异常值对线性回归模型的显著影响。
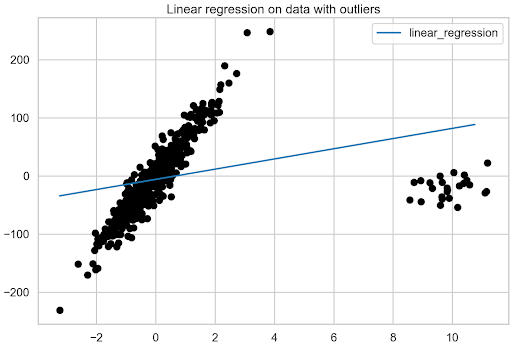 图 2 :线性回归模型对含有异常值的数据的拟合
图 2 :线性回归模型对含有异常值的数据的拟合
使用线性回归获得了基准模型。现在是时候转向稳健回归算法了。
Huber regression 是稳健回归算法的一个示例,该算法为被识别为异常值的观察值分配较少的权重。为此,它在优化例程中使用 Huber 损耗。下面让我们更好地了解一下这个模型中实际发生了什么。
Huber 回归最小化以下损失函数:
其中,表示标准差,
表示特征集,
是回归的目标变量,
是估计系数的向量,
是正则化参数。该公式还表明,根据 Huber 损失,对异常值的处理与常规观测不同:
Huber 损失通过考虑残差来识别异常值,用表示。如果观察被认为是规则的(因为残差的绝对值小于某个阈值
),然后应用平方损失函数。否则,将观察值视为异常值,并应用绝对损失。话虽如此,胡伯损失基本上是平方损失函数和绝对损失函数的组合。
好奇的读者可能会注意到,第一个方程类似于 Ridge regression ,即包括 L2 正则化。 Huber 回归和岭回归的区别在于异常值的处理。
通过分析两种常用回归评估指标:均方误差( MSE )和平均绝对误差( MAE )之间的差异,您可能会认识到这种损失函数的方法。与 Huber 损失的含义类似,我建议在处理异常值时使用 MAE ,因为它不会像平方损失那样严重地惩罚这些观察值。
与前一点相关的是,优化平方损失会导致均值周围的无偏估计,而绝对差会导致中值周围的无偏估计。中位数对异常值的鲁棒性要比平均值强得多,因此预计这将提供一个偏差较小的估计。
使用默认值 1.35 ,这决定了回归对异常值的敏感性。 Huber ( 2004 )表明,当误差服从正态分布且
= 1 和
= 1.35 时,相对于 OLS 回归,效率达到 95% 。
对于您自己的用例,我建议使用网格搜索等方法调整超参数alpha和epsilon。
使用以下示例将 Huber 回归拟合到数据:
huber = HuberRegressor().fit(X, y) fit_df["huber_regression"] = huber.predict(plotline_X) coef_list.append(["huber_regression", huber.coef_[0]])
图 3 显示了拟合模型的最佳拟合线。
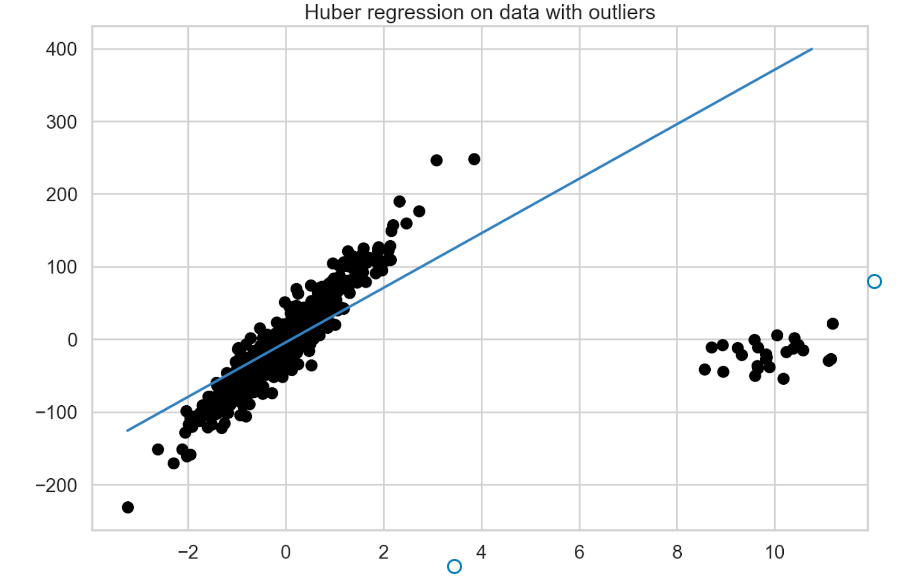 图 3 。 Huber 回归模型对含异常值数据的拟合
图 3 。 Huber 回归模型对含异常值数据的拟合
随机样本一致性( RANSAC )回归 是一种非确定性算法,试图将训练数据分为内联(可能受到噪声影响)和异常值。然后,它仅使用内联线估计最终模型。
RANSAC 是一种迭代算法,其中迭代包括以下步骤:
迭代执行步骤的次数最多,或者直到满足特殊停止标准。可以使用三个专用超参数设置这些标准。如前所述,最终模型是使用所有内部样本估计的。
将 RANSAC 回归模型与数据拟合。
ransac = RANSACRegressor(random_state=42).fit(X, y) fit_df["ransac_regression"] = ransac.predict(plotline_X) ransac_coef = ransac.estimator_.coef_ coef_list.append(["ransac_regression", ransac.estimator_.coef_[0]])
如您所见,恢复系数的过程有点复杂,因为首先需要使用estimator_访问模型的最终估计器(使用所有已识别的内联线训练的估计器)。由于它是一个LinearRegression对象,请像前面一样继续恢复系数。然后,绘制 RANSAC 回归拟合图(图 4 )。
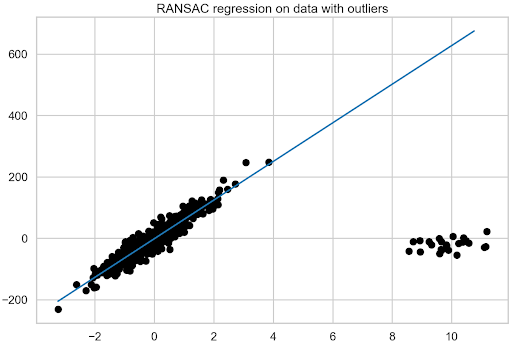 图 4 。 RANSAC 回归模型对含有异常值的数据的拟合
图 4 。 RANSAC 回归模型对含有异常值的数据的拟合
使用 RANSAC 回归,您还可以检查模型认为是内联值和离群值的观察值。首先,检查模型总共识别了多少异常值,然后检查手动引入的异常值中有多少与模型的决策重叠。训练数据的前 25 个观察值都是引入的异常值。
inlier_mask = ransac.inlier_mask_ outlier_mask = ~inlier_mask print(f"Total outliers: {sum(outlier_mask)}") print(f"Outliers you added yourself: {sum(outlier_mask[:N_OUTLIERS])} / {N_OUTLIERS}")
运行该示例将打印以下摘要:
Total outliers: 51 Outliers you added yourself: 25 / 25
大约 10% 的数据被确定为异常值,所有引入的观察结果都被正确归类为异常值。然后可以快速将内联线与异常值进行比较,以查看标记为异常值的其余 26 个观察值。
plt.scatter(X[inlier_mask], y[inlier_mask], color="blue", label="Inliers") plt.scatter(X[outlier_mask], y[outlier_mask], color="red", label="Outliers") plt.title("RANSAC - outliers vs inliers");
图 5 显示,距离原始数据的假设最佳拟合线最远的观测值被视为异常值。
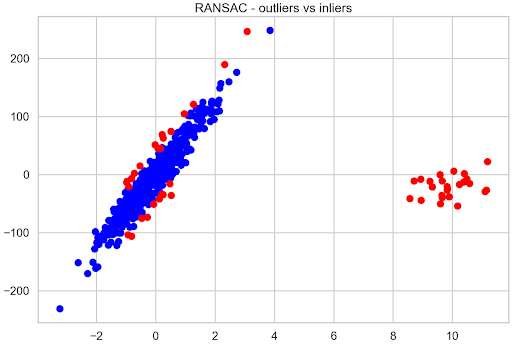 图 5 。与 RANSAC 算法识别的异常值进行比较的内联线
图 5 。与 RANSAC 算法识别的异常值进行比较的内联线
scikit-learn中可用的最后一种稳健回归算法是 Theil-Sen regression 。这是一种非参数回归方法,这意味着它不假设基础数据分布。简而言之,它涉及在训练数据子集上拟合多元回归模型,然后在最后一步聚合系数。
下面是算法的工作原理。首先,它计算从训练集 X 中的所有观察值创建的大小为 p (超参数n_subsamples)的子集上的最小二乘解(斜率和截距)。如果计算截距(可选),则必须满足以下条件p >= n_features + 1。直线的最终斜率(可能还有截距)定义为所有最小二乘解的(空间)中值。
该算法的一个可能缺点是计算复杂度,因为它可以考虑等于n_samples choose n_subsamples的最小二乘解总数,其中n_samples是 X 中的观测数。鉴于这一数字可能迅速扩大,可以做几件事:
此外,请注意,估计器的稳健性随着问题的维数迅速降低。要了解这在实践中的效果,请使用以下示例估计泰尔森回归:
theilsen = TheilSenRegressor(random_state=42).fit(X, y) fit_df["theilsen_regression"] = theilsen.predict(plotline_X) coef_list.append(["theilsen_regression", theilsen.coef_[0]])
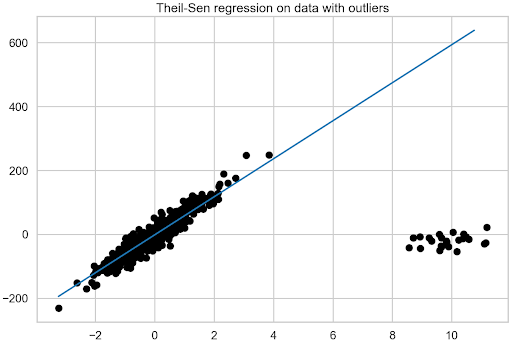 图 6 。泰尔森回归模型对含有异常值的数据的拟合
图 6 。泰尔森回归模型对含有异常值的数据的拟合
到目前为止,已经对包含异常值的数据拟合了三种稳健回归算法,并确定了各个最佳拟合线。现在是进行比较的时候了。
从图 7 的目视检查开始。为了显示太多行,未打印原始数据的拟合行。然而,考虑到大多数数据点的方向,很容易想象它是什么样子。显然, RANSAC 和泰尔森回归得到了最准确的最佳拟合线。
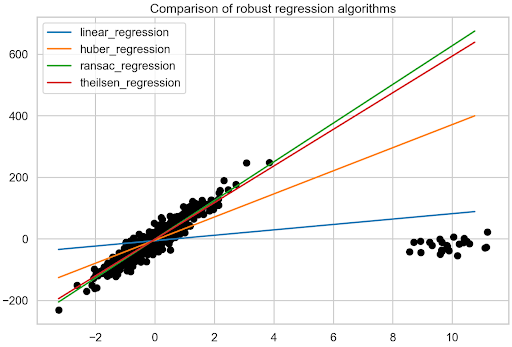 图 7 。所有考虑的回归模型的比较
图 7 。所有考虑的回归模型的比较
更准确地说,请查看估计系数。表 1 显示, RANSAC 回归结果最接近原始数据之一。有趣的是, 5% 的异常值对正则线性回归拟合的影响有多大。
| model | coefficient | |
| 0 | original_coef | 64.59 |
| 1 | linear_regression | 8.77 |
| 2 | huber_regression | 37.52 |
| 3 | ransac_regression | 62.85 |
| 4 | theilsen_regression | 59.49 |
表 1 。不同模型的系数与 Outle 数据拟合的比较 卢比
你可能会问哪种稳健回归算法最好?通常情况下,答案是“视情况而定”以下是一些指导原则,可以帮助您找到适合您具体问题的正确模型:
考虑到前面的所有信息,您还可以根据经验对所有三种稳健回归算法进行实验,看看哪一种最适合您的数据。
你可以在我的 /erykml GitHub repo 中找到本文中使用的代码。我期待着收到你的评论。