1,040
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享这是我参加朝闻道知识分享大赛的第4篇文章
目录
import torch
x = torch.randn(100) # 生成100个标准正态分布随机数
y = 3*x+2
k = torch.randn(1)
b = torch.randn(1)
print(f'k:{k},b:{b}')
![]()
# 定义模型(函数表达式)
def linear(x,k,b):
return k*x+b
# 定义损失函数(误差函数)
def loss_fun(y_true,y_pred):
return 1/2 * torch.sum(torch.square(y_true-y_pred))
y_pred = linear(x,k,b)
error = loss_fun(y,y_pred)
print(error)
![]()
# 求参数关于损失的梯度
d_k=(y - y_pred )*(-1)*x
d_b = (y - y_pred )*(-1)
# 超参数定义
# 定义学习率
lr=0.5
# 更新参数
k = k - torch.sum(d_k) * lr
b = b - torch.sum(d_b) * lr
print(f'k:{k},b={b}')
# 定义超参数
# 定义最大迭代次数
epochs = 100
for epoch in range (epochs):
#向前计算
y_pred = linear(x,k,b)
errpr = loss_fun(y,y_pred)
#反向传播计算梯度
d_k = (y - y_pred) * (-1) *x
d_b = (y - y_pred) * (-1)
#更新参数
k = k-torch.sum(d_k) * lr
b = b-torch.sum(d_b) * lr
print(f"epoch{epoch+1},loss:{error},k:{k},b:{b}")
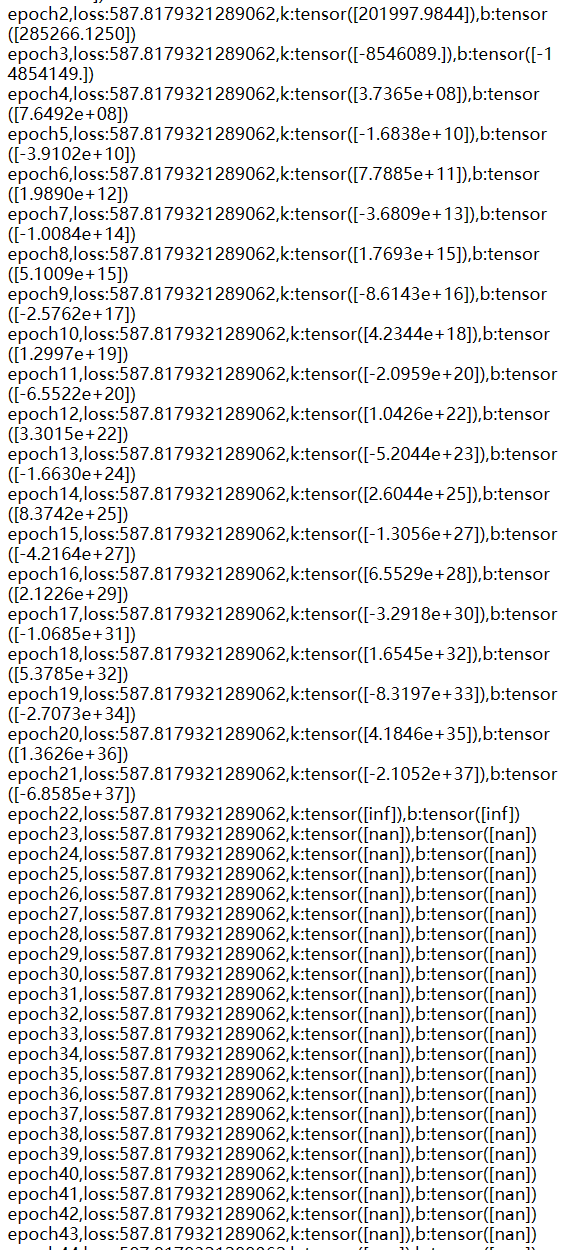
出现梯度爆炸现象,说明学习率设置得过大
# 重新定义学习率
lr=0.01
# 重新初始化参数
k = torch.randn(1)
b = torch.randn(1)
#再次迭代
for epoch in range (epochs):
#向前计算
y_pred = linear(x,k,b)
errpr = loss_fun(y,y_pred)
#反向传播计算梯度
d_k = (y - y_pred) * (-1) *x
d_b = (y - y_pred) * (-1)
#更新参数
k = k-torch.sum(d_k) * lr
b = b-torch.sum(d_b) * lr
print(f"epoch:{epoch+1},loss:{error},k:{k},b:{b}")
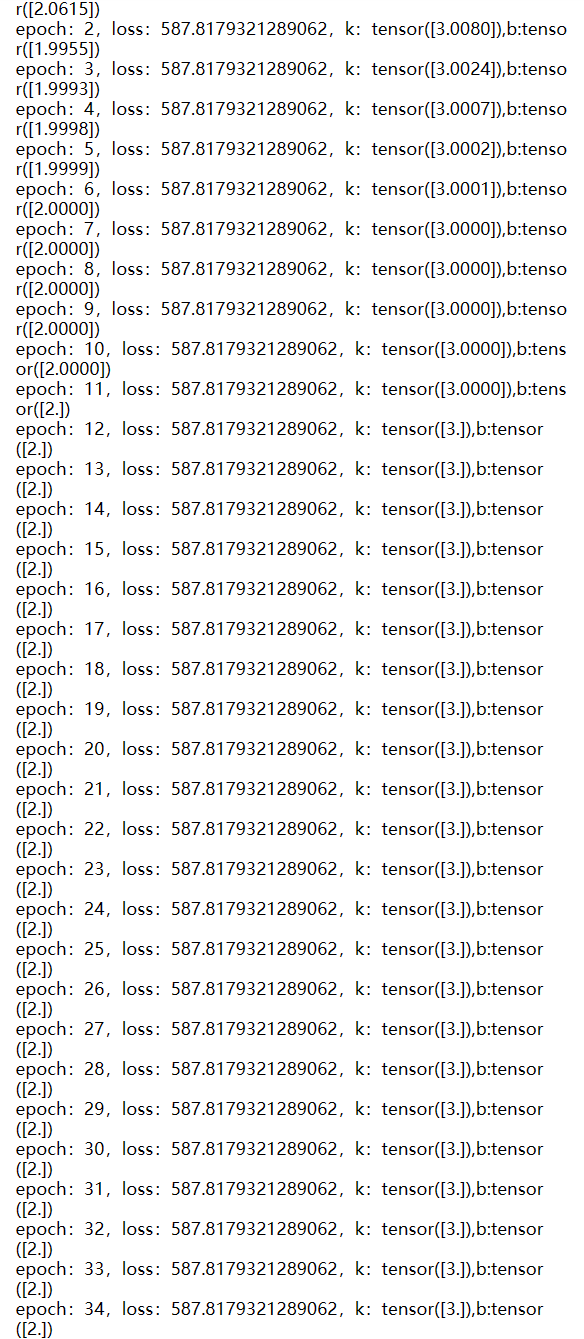
为了减少我们写代码的数量,我们也可以使用使用PyTorch的自动求导机制计算
# 重新初始化参
k = torch.randn(1,requires_grad=True)
b = torch.randn(1,requires_grad=True)
print(f'k:{k},b:{b}')

y_pred = linear(x,k,b)
error = loss_fun(y,y_pred)
#反向传播计算梯度
error.backward()
d_k = k.grad
#再次迭代
for epoch in range (epochs):
#向前计算
y_pred = linear(x,k,b)
error = loss_fun(y,y_pred)
#反向传播计算梯度
error.backward(retain_graph=True)
d_k = k.grad
d_b = b.grad
#更新参数
k.data-=d_k * lr
b.data-=d_b * lr
#梯度置零
k.grad.data.zero_()
b.grad.data.zero_()
print(f"epoch:{epoch+1},loss:{error},k:{k},b:{b}")
