564
社区成员
 发帖
发帖 与我相关
与我相关 我的任务
我的任务 分享
分享主讲老师:张磊、冯骏
Private Information Retrieval PIR,官名【隐私信息检索】
顾名思义,匿踪查询首先是要查询,但是又希望隐匿踪迹,不能让被查询方知道你查到了什么。假设检查部门正在对某些可疑人员进行调查,但是由于被调查者具备一定的反侦察经验,如果检查部门直接去各个系统里面对这个人进行精准查询,会激发被调查者的警觉,进而出现不可控的局面。所以在这种情况下检查部门需要「一种不对外泄露查询条件和查询结果的隐私计算技术」。
例如,用户查询服务端数据库中的数据,但服务端不知道用户查询的是哪些数据。

PIR是多方安全计算中非常实用的一门技术与应用,可以用来保护用户的查询隐私,进而也可以保护用户的查询结果。其目标是保证用户向数据源方提交查询请求时,在查询信息不被感知与泄漏的前提下完成查询。即对于数据源方来说,「只知道有查询到来,但是不知道真正的查询条件、也就不知道对方查了什么」。
按服务器数量分类
按查询类型分类
按照实现技术分类
其中基于不经意传输的PIR与基于同态加密的PIR方案是需要检索用户提前感知被检索数据在数据库中位置(索引号),这块可以通过隐私求交的方式实现。
性能分析
基于index的PIR
基于不经意传输的PIR实现过程如下,使用的是n选1的OT协议。(注:已知查询元素的位置)
首先,假设Server端有$n$条数据,那么将会生成与$n$条数据一一对应的$n$个RSA公私钥对$((d_{1}^{PK},d_{1}^{SK}),…,(d_{n}^{PK}, d_{n}^{SK}))$,并将$n$个私钥保留,将$n$个公钥$(d_1^{PK}, …, d_n^{PK})$发送给Client端,私钥保留在Server。
然后,Client端随机生成一个对称加密的秘钥$key$,假设用户要检索第$t$条数据,则用收到的第$t$个RSA公钥$d_{t}^{PK}$加密这个$key$,将加密结果$R$发送给Server
然后,Server端用保留的$n$个RSA私钥$(d_1^{SK}, …, d_n^{SK})$,依次尝试解密$R$,获得$n$个解密结果,依次为$(key_1,key_2,…, key_t, …,key_n)$。
然后,$Server$端利用对称加密算法(此处为AES算法),利用$(s_1,s_2,…,s_{t},…,s_{n})$针对$n$条数据进行一一对应加密,将产生的密文消息$(s_1,s_2,…,s_t,…,s_n)$发送给用户。
最后,客户端使用第2步中的$key$,对$(s_1,s_2,…,s_t,…,s_n)$消息中的第$t$条密文$s_t$进行对称解密,则得到想要检索的第$t$条原始明文消息$$m_t$$。
基于Index的PIR
基于同态加密的PIR实现采用Paillier加法半同态加密算法。
此处简述下Paillier算法的三个重要特点:
基于paillier同态加密的PIR实现过程有五个重要步骤
首先,Client端生成同态加密公私钥$$(h^{PK}, h^{SK})$$
然后,假设Server端有$n$条数据$(m_1,…,m_t,…,m_n)$,客户端要检索第$t$条数据。那么Client产生一个$n$维密文向量$(s_1,…, s_t, …, s_n)$,生成规则如下:
然后,Client将$n$维密文向量$(s_1, …,s_t,…,s_n)$和公钥$h^{PK}$发送给服务端;
然后,Server将$n$维密文向量$(s_1,…,s_t,…,s_n)$和$n$条明文数据集做向量内积运算,得到密文结果$R$,并且将$R$发送给Client。(同态加密算法的性质是密文计算结果解密后与明文计算结果相等),密文的计算公式相当于是$R=E(m_1\times0+…+m_t \times1+…+m_n\times 0)=E(m_t)$
最后,Client利用私钥$h^{PK}$对$R$进行解密,得到想要检索的第$t$条原始明文消息。
前面的场景中,我们都是先通过隐私求交进行获取待查询数据在数据源中的位置,但是如果没有位置信息,是否可以进行查询呢?答案就是根据关键词进行查询,此类方案又称keyword PIR,可以利用Paillier同态加密+拉格朗日插值多项式实现。
首先,假设Server端有明文数据集$((k_1,v_1), …, (k_t, v_t), …, (k_n,v_n))$。接下来对此明文数据集进行拉格朗日多项式插值法生成最终多项式$H(X)$,同时生成标识多项式$F(X)$。(当取存在的点的时候,计算结果为0,否则为1);
$$
H(X)=a_0+a_1x+a_2x^2+...+a_nx^n
$$
那么,$H(k_1)=v_1$,$H(k_2)=v_2$,$H(k_n)=v_n$。
$$
F(x)=(x-k_1)(x-k_2)...(x-k_n)=c_0+c_1x+c_2x^2+...+c_nx_n
$$
因此,$F(k_1)=0, F(k_2)=0, …, F(k_n)=0$
然后,Client生成同态加密公私钥$(h^{PK}, h^{SK})$
然后,假设Client要查询$k_t$,同时使用$h^{PK}$分别加密$k_t$的1次方到n次方$(E(k_t), E(k_t^2), …E(k_t^n))$,发送给Server。
然后,Server利用密文向量$(E(k_t), E(k_t^2), …E(k_t^n))$,代入到函数$F(X)$和$H(x)$,分别计算同态密文$E(F(x_t))$和$E(H(x_t))$,将计算结果发送给用户。
最后,Client通过私钥$h^{SK}$对两条密文进行解密,如果$F(x_t)=0$,则$H(x_t)$即为检索结果;否则检索结果为空。
Private Information Retrieval PIR
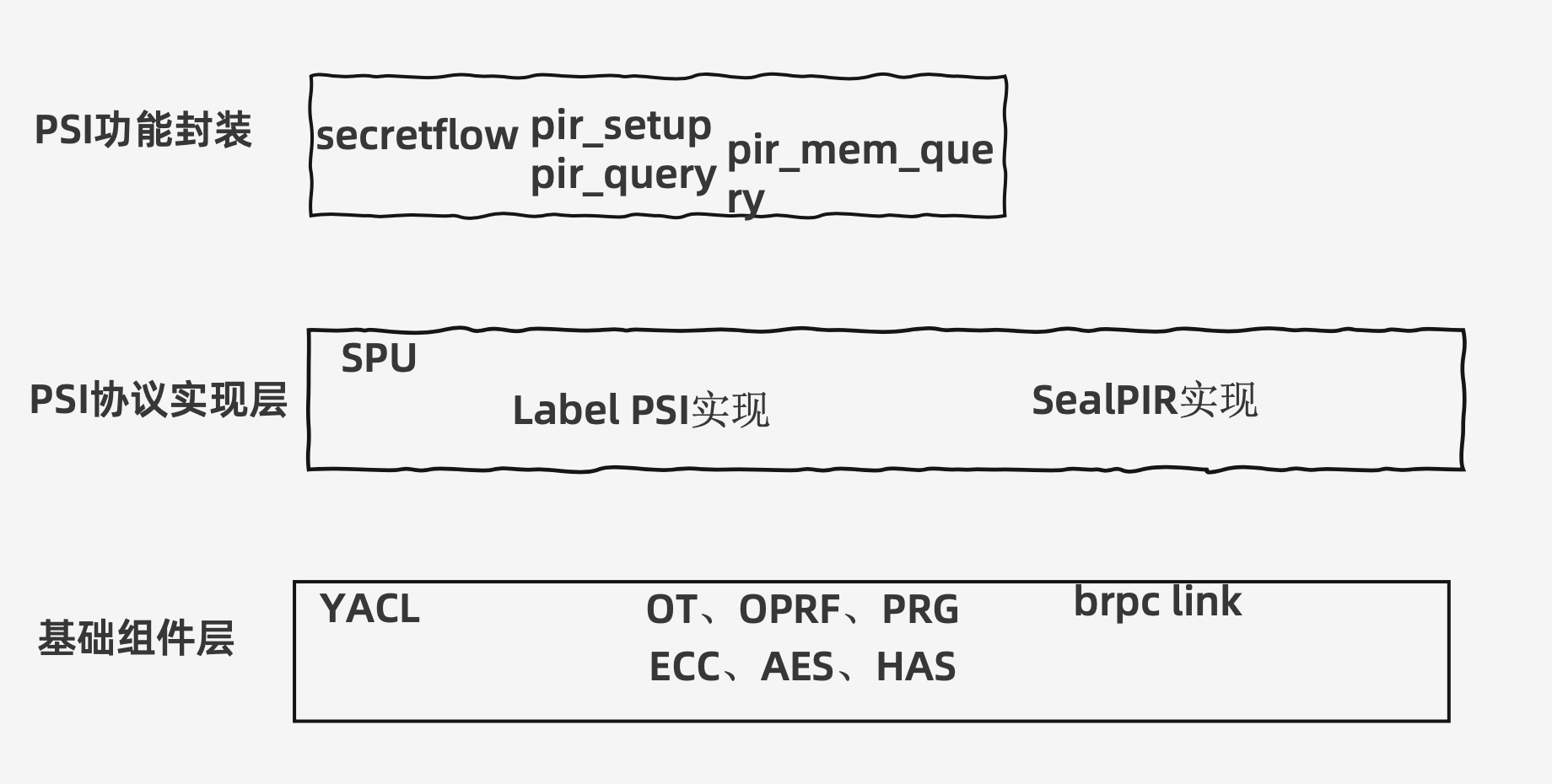
功能封装
https://github.com/secretflow/secretflow/blob/v1.5.0.dev240319/secretflow/device/device/spu.py#L1191
pir_setuppir_querypir_mem_queryPSI协议实现层
基础组件YACL
涉及到底层的密码学算法
主要位于SPU的代码库

https://github.com/secretflow/secretflow/blob/v1.5.0.dev240319/secretflow/device/device/spu.py#L1191
参数说明:
server:Server端对应的party_name
input_path:服务端数据文件路径,建议绝对路径
key_columns:key对应的列名
label_columns:Label对应的列名,若多列则用逗号分开
opera_key_path:服务端ecc密钥文件,32B,二进制文件
setup_path:Offline/Setup phase output data dir. Use an absolute path
num_per_query:每次查询的id数量,一般设置为1.
目前如果设置为大于1的数$k$,则会调用$k$次该接口。
label_max_len:Label数据拼接后填充到固定的长度大小,也就是label的最大字节数
bucket_size: 不可区分度,Split data bucket to do pir query
示例:
reports = spu.pir_setup(
server='bob', input_path='/path/B_PIR_DATA.csv', key_columns='id',
label_columns=['register_date','age'],
oprf_key_path='/path/oprf_key.bin',
setup_path='/path/setup_path',
num_per_query=1,
label_max_len=18
)
https://github.com/secretflow/secretflow/blob/v1.5.0.dev240319/secretflow/device/device/spu.py#L1253
配置:
server:Server端对应的party_nameclient:Client端对应的party_nameclient_input_path:Client端id对应的csv文件路径 client_key_columns: Key对应的列名 client_output_path:PIR查询结果输出的文件路径 server_setup_path : 服务端ecc密钥文件,32B,二进制文件 示例
spu.pir_query(
server='alice',
client='bob',
server_setup_path=f'{current_dir}/alice_setup',
client_key_columns=["name"],
client_input_path=f"{current_dir}/bob_pir_dataset.csv",
client_output_path=f"{current_dir}/bob_pir_result.csv"
)
基于BFV的同态方案
多项式次数$N$
明文模$t$
密文模$q$
Expansion Rate:$2\times log(q)/log(t)$
明文
$$
R_t=\mathbb{Z}_t[x]/(x^N+1)
$$
$\mathbb{Z}_n$表示模n的整数环
$$
a_0+a_1x+...+a_{N-1}x^{N-1}
$$
密文加法:若明文$p_1(x), p_2(x)$的密文为$c_1$和$c_2$,则$c_1+c_2$是$p_1(x)+p_2(x)$的密文
明文乘密文:明文$p_1(x)$的密文为$c$,$p_2(x)$是另一个数的明文,则$p_2(x) \times c$是$p_1(x) \times p_2(x)$的密文。
替换:明文$p(x)$的密文为$c$,奇数为$k$
$Sub(c,k)$是$p(x^k)$的密文,例如:$p(x)=7+x^2+2x^3$
$Sub(c,3)$,得到$p(x^3)=7+(x^3)^2+2(x^3)^3=7+x^6+2x^9$的密文
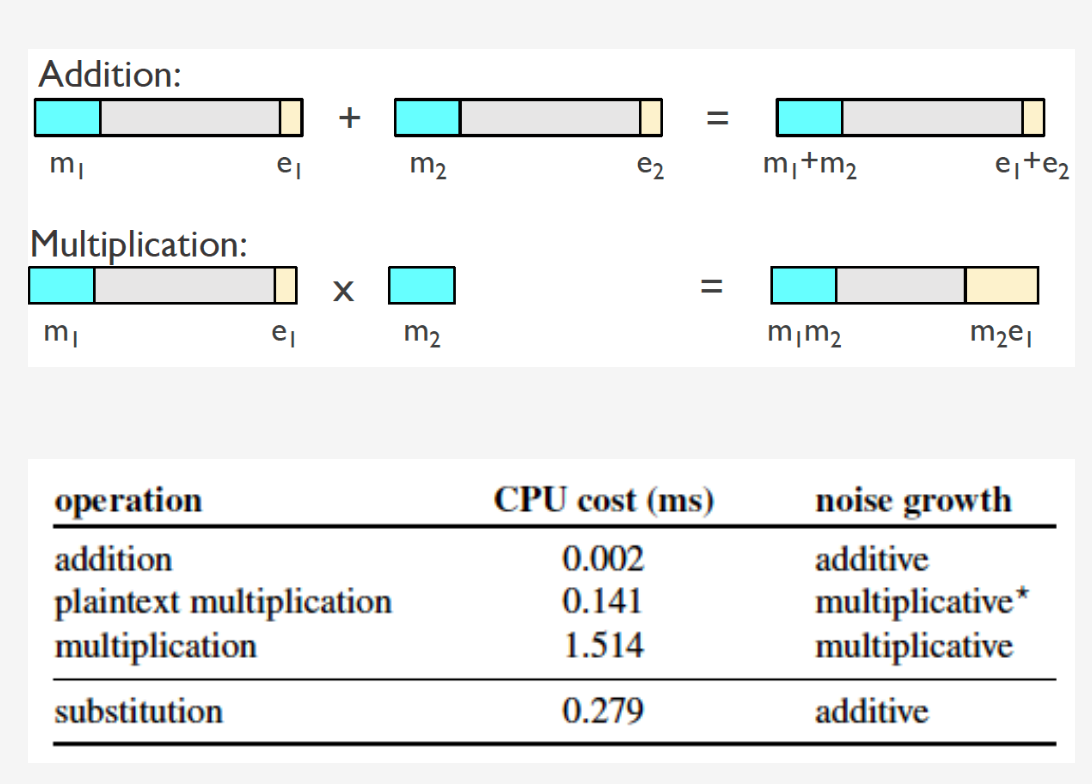
同态计算的噪声增长
同态乘法,噪声增长较大,而且用时相对较久。SealPIR中尽量避免使用乘法。

a. Client端将查询向量使用同态算法进行加密得到$[E(0), …,E(1), E(0)]$,将加密后信息发给Server端;
b. Server将本方数据$B_1, …, B_{i-1}, B_{i}, B_{i+1},…B_{n}$与Client端发送的数据进行内积。将结果$E(B_i)$发送给Client。
c. Client对$E(B_i)$解密,获得结果。
查询的db_index转换为plaintext_index

例如将原始数据库中的$[B_1,B_2,B_3]$压缩到明文多项式$P_1=a_0+a_1x+…+a_{N-1}x^{N-1}$,$[B_4,B_5,B_6]$压缩到明文数据库$P_2 = b_0+b_1x+…+b_{N-1}x^{N-1}$,等等。
Client端查询,需要将数据库查询的index,转换为多项式查询的index
例如对$B_4$进行查询,需要转换为查询多项式$P_2$
Server端返回$P_2$的加密值给Client端
Client端进行同态解密,解密后得到一个明文多项式$b_0+b_1x+…+b_{N-1}x^{N-1}$,根据pack的偏移,找到$B_4$对应的系数。将其拼接为一个明文数据。
多项式次数:8192
明文模:17bit
DB数据长度:288B
Ceil($\frac{288*8}{16}=144$)
Floor($\frac{8192}{144}=56$)
每个多项式可以pack 56个原始数据。
实现Symmetric PIR时,不使用packing
显著减少通信量,server端可通过计算expand得到查询密文向量
客户端生成查询密文
查询向量${0,0,…,1,…,0}$转换为同态明文plaintext:$x^{query_{index}}=a_0+a_1x+…+a_{N-1}x^{N-1}$
$a_i=0, i\ne query_{index}$,$a_i = 1, i = query_{index}$
加密$Enc(a_0+a_1x+…+a_{N-1}x^{N-1})=Enc(x^{query_{index}})$
Server端通过执行Expand算法,得到密文向量:$Enc(0), Enc(0), …, Enc(1), …, Enc(0)$
每个明文可以pack多个原始数据,例如上述可以pack56个。通过一个明文查询,可以对$8192 \times 56=458752$个原始数据进行查询。
以二维数据为例
2维查询将数据转换为$\sqrt{n} \times \sqrt{n}$的矩阵,减少expand计算量

$\sqrt{n} \times \sqrt{n}$的矩阵$M$,其中$\sqrt{n} \le 8192$
$V_c$是密文查询向量,$A_c=M·V_c$,$A_c$是$\sqrt{n}\times 1$的密文列向量。
$F=2\times log(q)/log(t)$是扩张因子,$F=2\times log(218)/log(16) \approx 28$
使用cuckoo hash支持同时进行多个查询

SealPIR 中给出了通过cuckooHash进行多个查询的算法,可以提高查询效率。cuckooHash选取3个hash,bin的个数为$1.5k$,具体算法,如下:
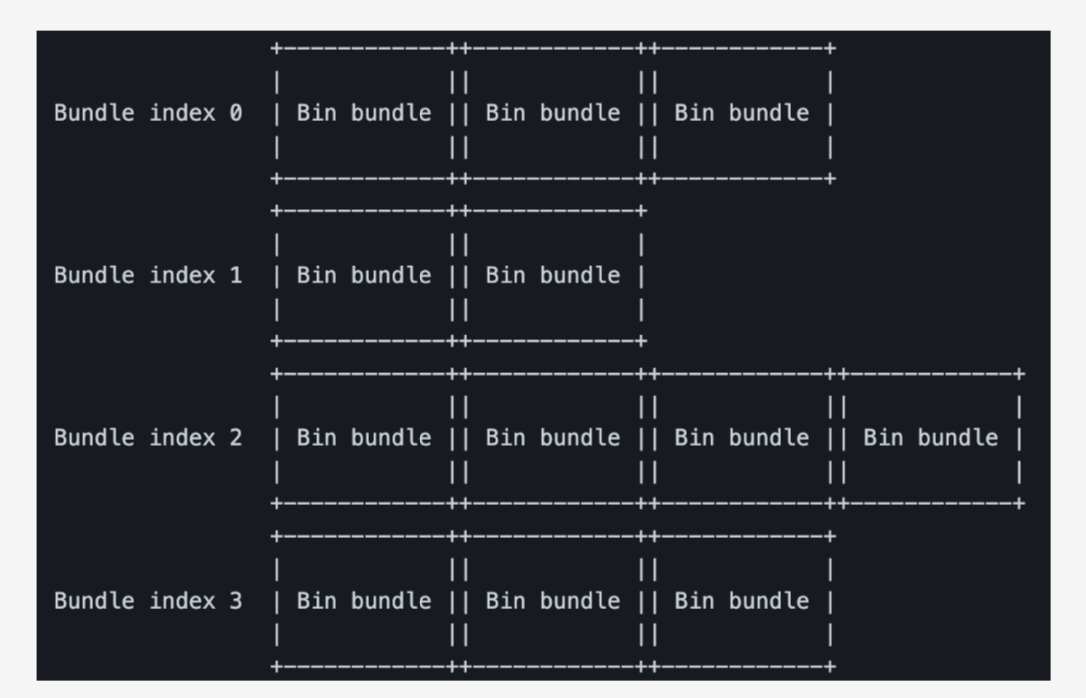
Server setup
对DB中n个元素,分别计算cuckooHash的3个Hash,得到3个bin index,插入到 3个bin index中
Client query
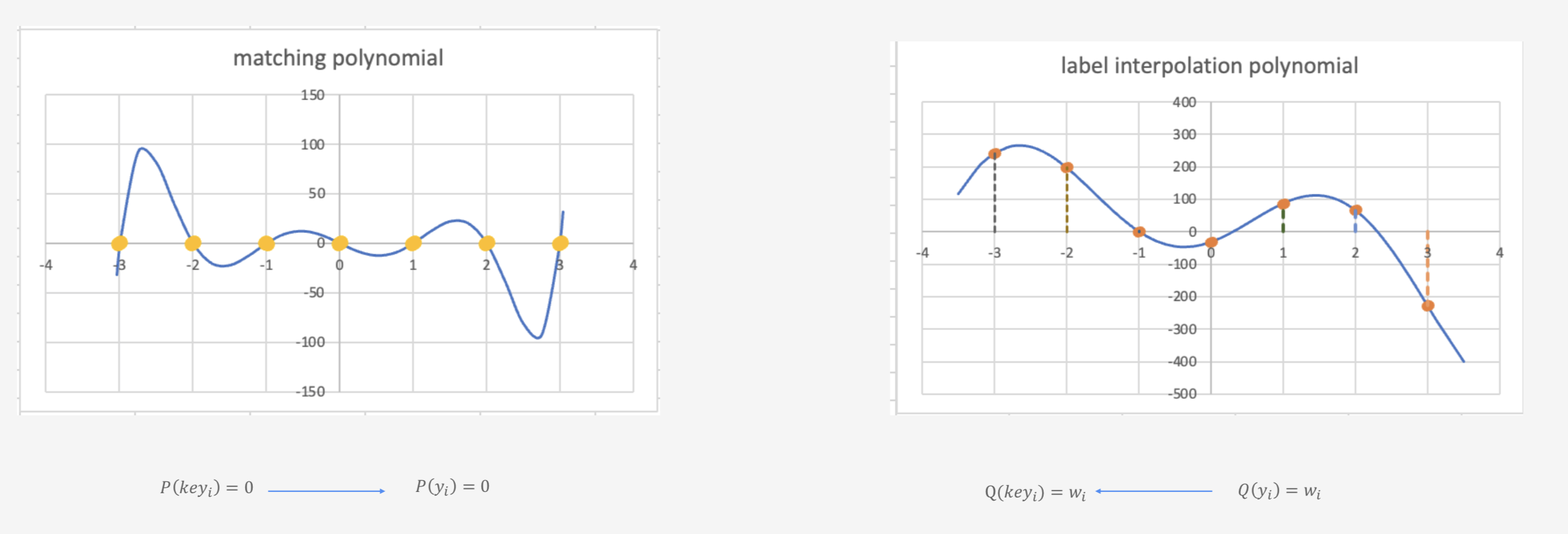
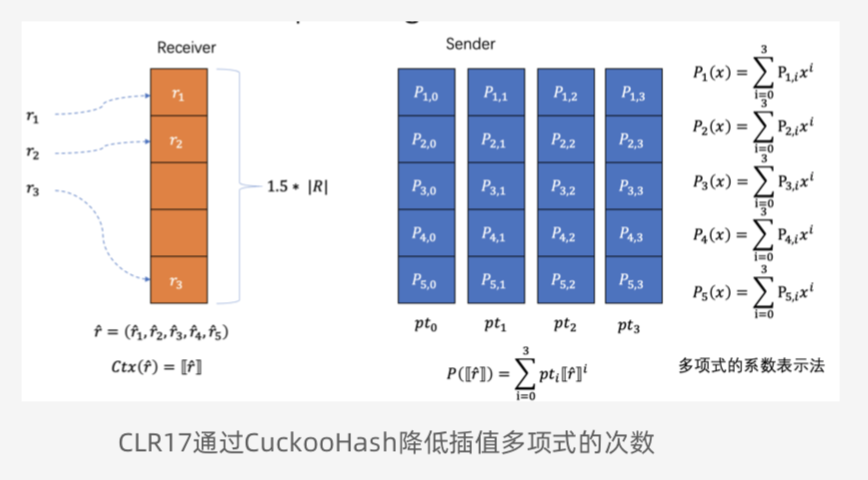
核心思想:点值表示得到插值多项式系数表示
在匹配多项式$P(key_i)=0$的情况下,对应的插值多项式$Q(key_i)=w_i$对应带查询的value
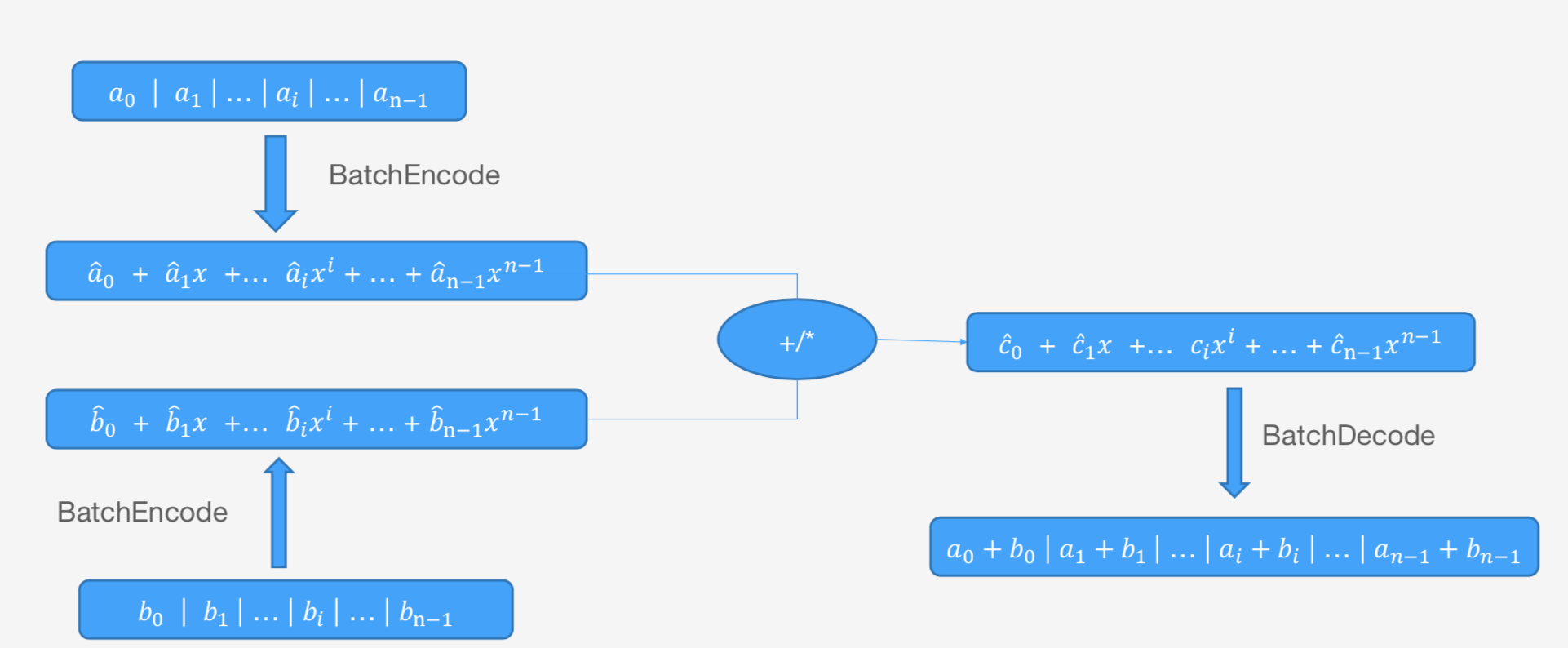
Labeled PSI的原理可参考下面的论文:

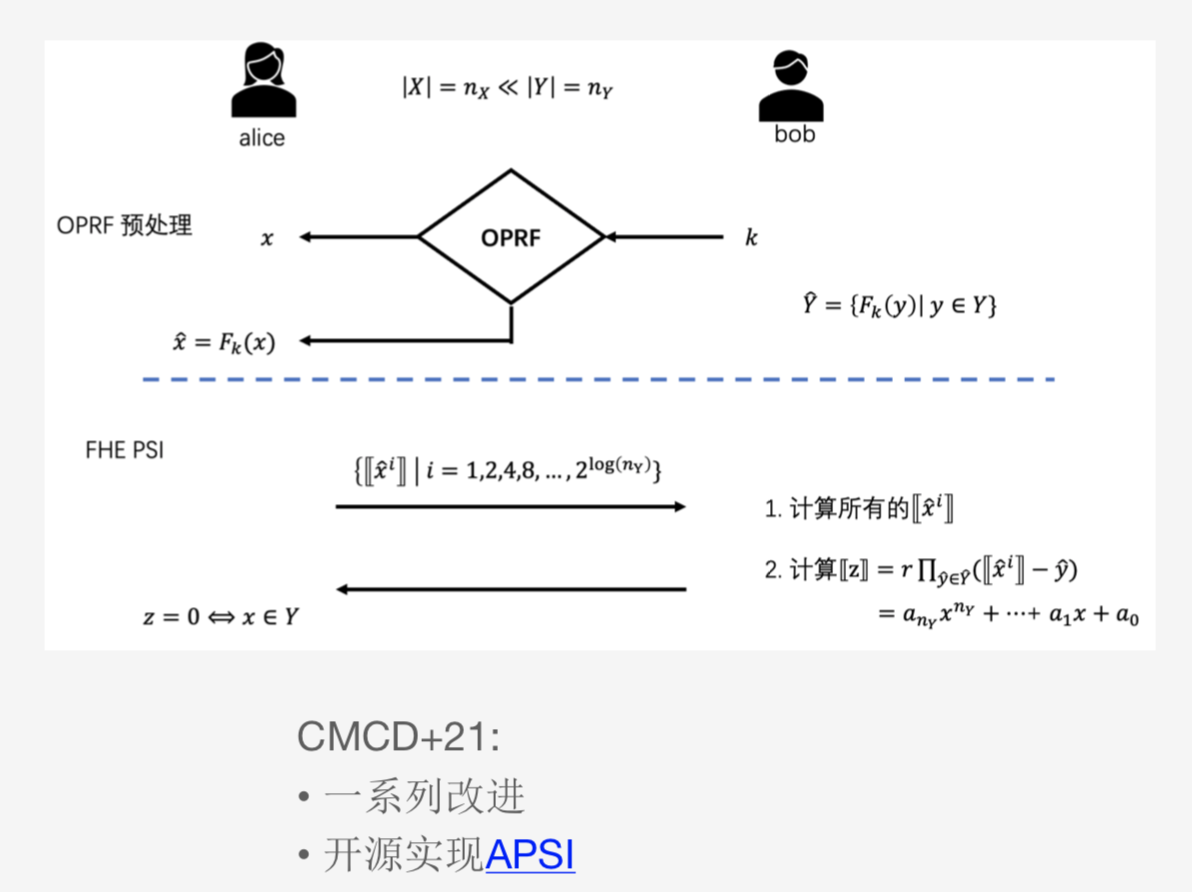

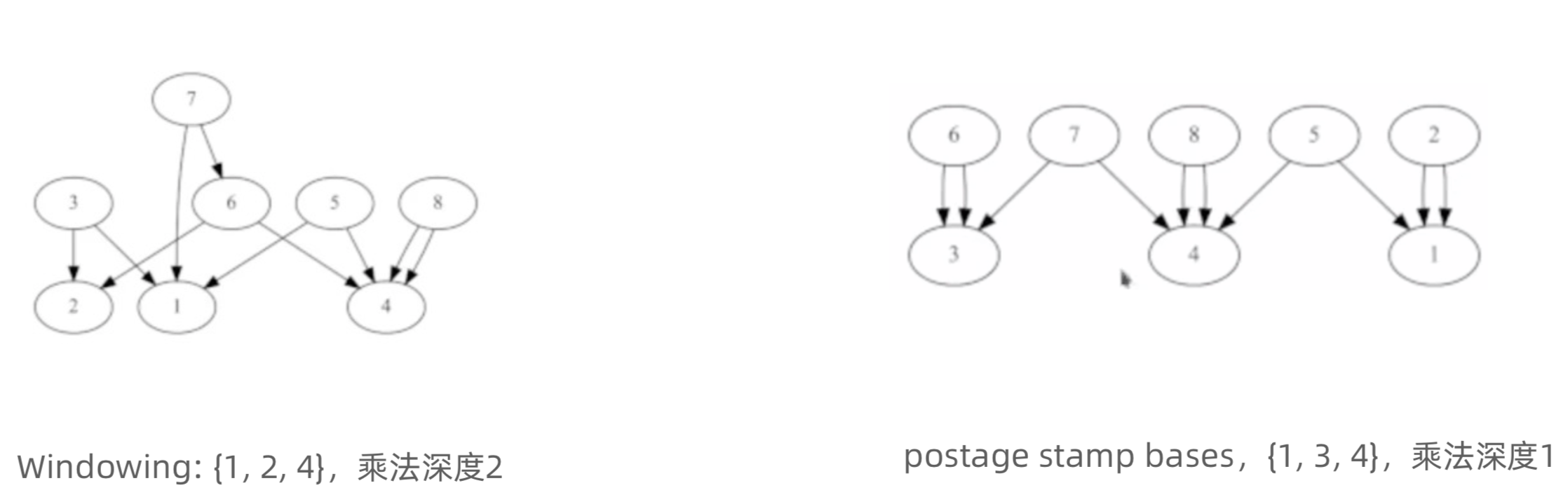
使用extremal postage stamp bases减少通信量

以微软的开源代码功能为核心
OPRF采用隐语的实现:
支持的ecc曲线包括:FourQ, Secp256k1, SM2


客户端向服务端请求参数
执行oprf协议
计算查询值的同态密文幂集合
使用同态私钥解密服务端返回的同态密文
满足匹配条件时,使用oprf的后128bit解密得到label


下载secretnote
pip install secretnote -i https://pypi.tuna.tsinghua.edu.cn/simple
每个参与方需要在容器中手动启动secretnote
这里,由于我们使用的是host模式,端口被其他服务占用,额外修改了端口
secretnote --port=35000
端口统计
| alice | bob | |
|---|---|---|
| ray head | 35000 | 35600 |
| Secretnote | 25500 | 25002 |
数据集文件CSV
secretnote启动的目录下的所有csv文件,会显示在前端页面上:
资源占用情况
右上角有一个小图标,可以查看各个计算节点的状态情况。


Python 3.10
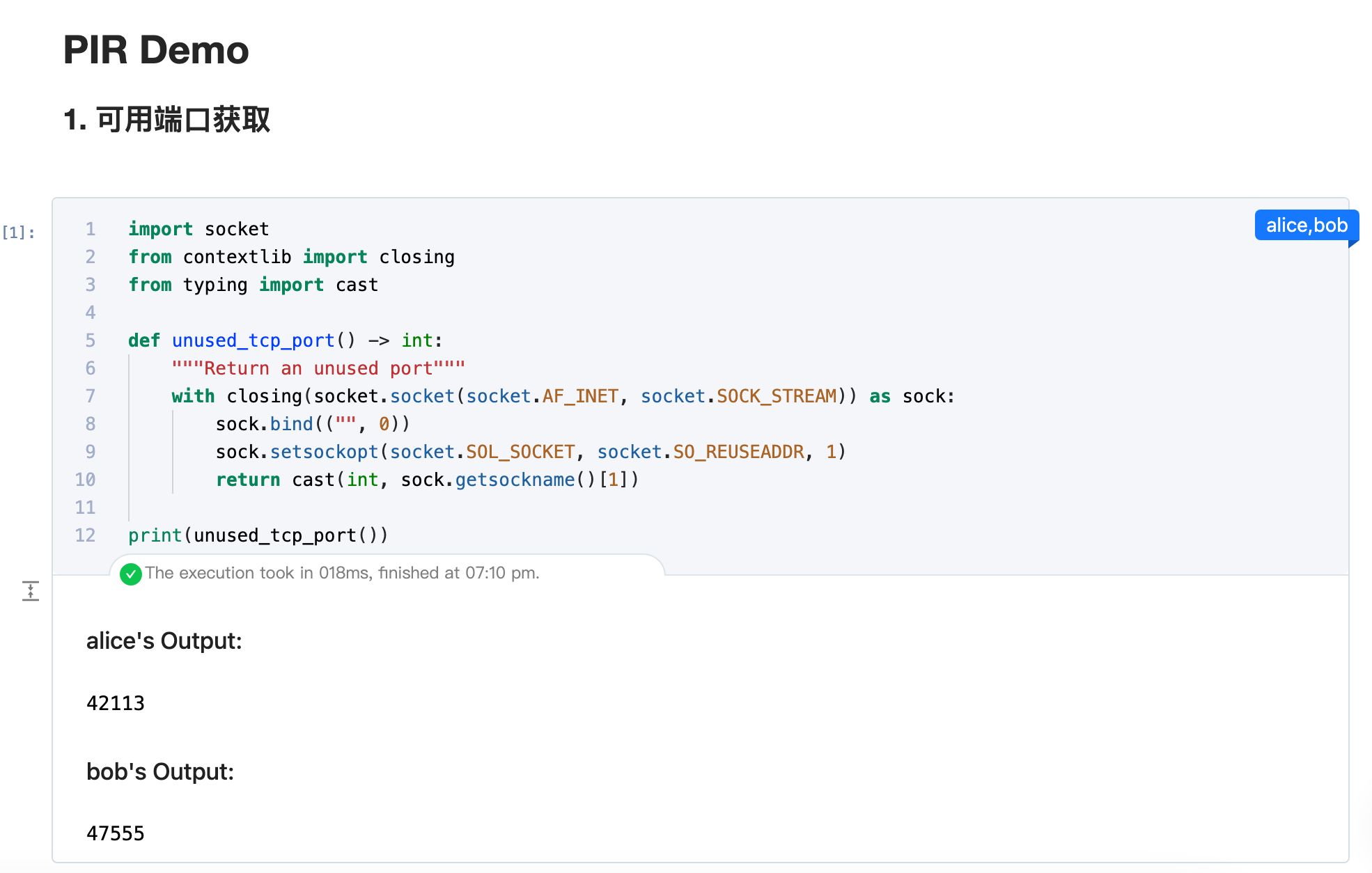
寻找未使用的port,这些端口会被用于alice和bob的ray-fed通信地址
import socket
from contextlib import closing
from typing import cast
def unused_tcp_port() -> int:
"""Return an unused port"""
with closing(socket.socket(socket.AF_INET, socket.SOCK_STREAM)) as sock:
sock.bind(("", 0))
sock.setsockopt(socket.SOL_SOCKET, socket.SO_REUSEADDR, 1)
return cast(int, sock.getsockname()[1])
print(unused_tcp_port())
可以看到alice和bob随机找到的未使用的端口是不同的:
Ray-fed的启动
cluster_config中address声明每个参与方进行ray-fed通信的地址,listen_addr用于参与方自己用。
sf.init()中的address为ray的head节点的ip和端口号。如果填入local,会在本地启动一个ray集群。
alice
import secretflow as sf
cluster_config = {
"parties": {
"alice": {
# replace with alice's real address
"address": "Alice_IP:42113",
"listen_addr": "0.0.0.0:42113"
},
"bob": {
"address": "Bob_IP:47555",
"listen_addr": "0.0.0.0:47555"
},
},
'self_party': 'alice'
}
sf.shutdown()
sf.init(address="Alice_RAY_IP:RAY_PORT", cluster_config=cluster_config)
Alice_IP为alice的真实IPAlice_RAY_IP为alice的ray head的IP,RAY_PORT为ray启动的端口。bob
import secretflow as sf
cluster_config = {
"parties": {
"alice": {
# replace with alice's real address
"address": "Alice_IP:42113",
"listen_addr": "0.0.0.0:42113"
},
"bob": {
"address": "Bob_IP:47555",
"listen_addr": "0.0.0.0:47555"
},
},
'self_party': 'bob'
}
sf.shutdown()
sf.init(address="BOB_RAY_IP:RAY_PORT", cluster_config=cluster_config)
Bob_IP为Bob的真实IP
Bob_RAY_IP为bob的ray head的IP,RAY_PORT为ray启动的端口。
注意:执行时需要选择两个cell同时运行
SPU 配置
这里的address为新的地址,不要和之前设置的冲突了。
import spu
cluster_conf = {
"nodes": [
{
"party": "alice",
"address": "alice:36247"
},
{
"party": "bob",
"address": "bob:53635"
},
],
"runtime_config": {
"protocol": spu.spu_pb2.SEMI2K,
"field": spu.spu_pb2.FM128,
"sigmoid_mode": spu.spu_pb2.RuntimeConfig.SIGMOID_REAL,
},
}
spu = sf.SPU(
cluster_def=cluster_conf,
link_desc={
"connect_retry_times": 60,
"connect_retry_interval_ms": 1000
},
)
runtime_config设置PSI/PIR相关的配置link_desc配置网络不佳时的一些处理措施。 Server(Sender)一般为数据库,Client(Receiver)为请求方。demo中将Alice作为Server,Bob作为Client。

准备alice方需要的secret key
进入alice所在的容器,在alice的工作目录下调用openssl rand 32 > ~/alice_oprf_key:

demo中将Alice作为Server,Bob作为Client
两方一起运行,并设置相关参数。具体参数说明请看之前的介绍。
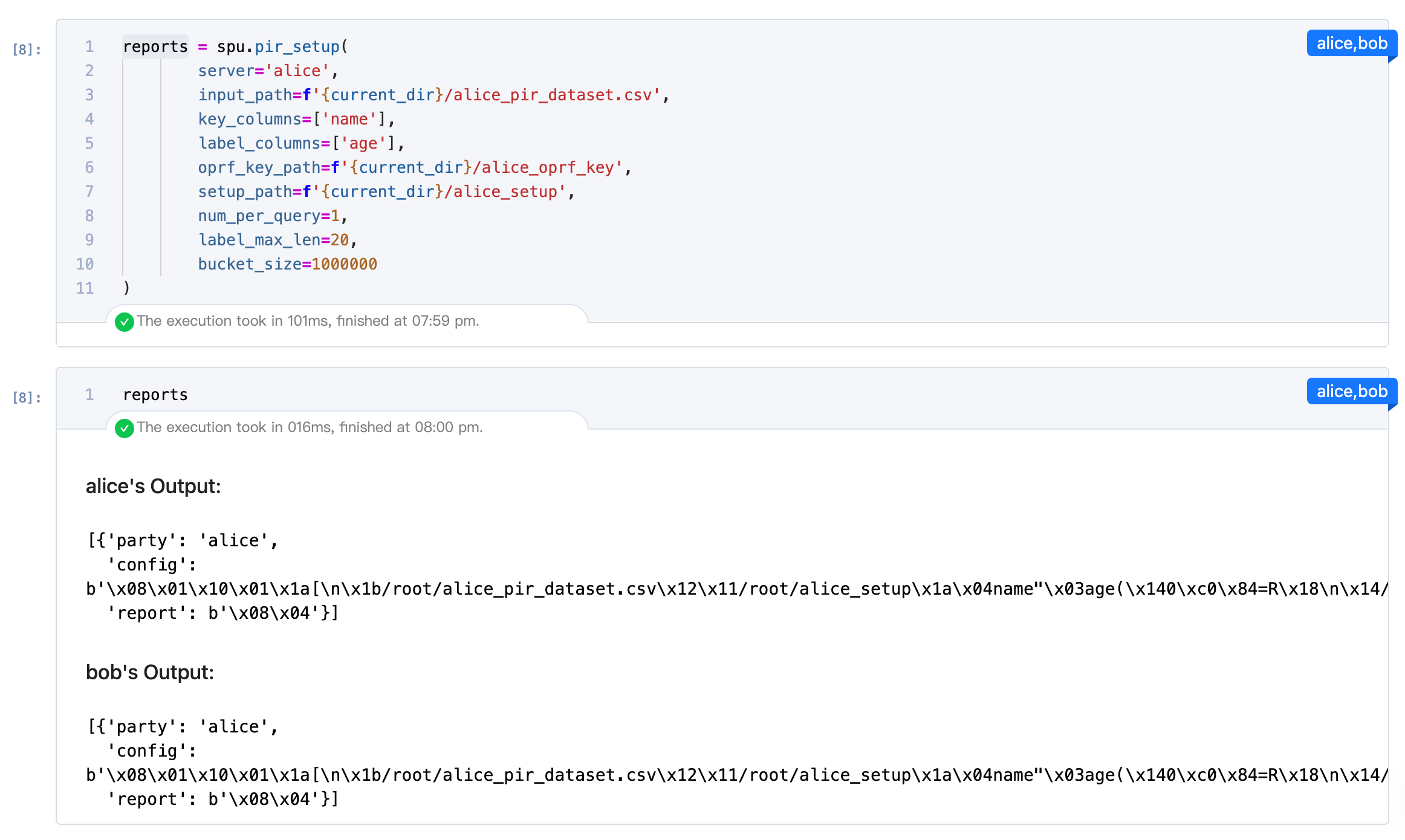
可以看到Alice设定的setup_path目录下,多了一些文件。而Bob是没有的。

设定相关的参数后,执行下列代码:

查看client_output_path对应的目录,可以看到:
