第6课笔记：逻辑回归LR与广义线性模型GLM开发实践

[m0_67646513]

背景知识-LR/GLM应用场景及原理

广义线性模型建模场景举例

一、二分类问题：逻辑回归

1. 对数据进行二元分类：例如对病人的数据进行疾病诊断。
2. 预测某件事情发生的概率：例如预测一个网站的用户变成付费用户的概率。

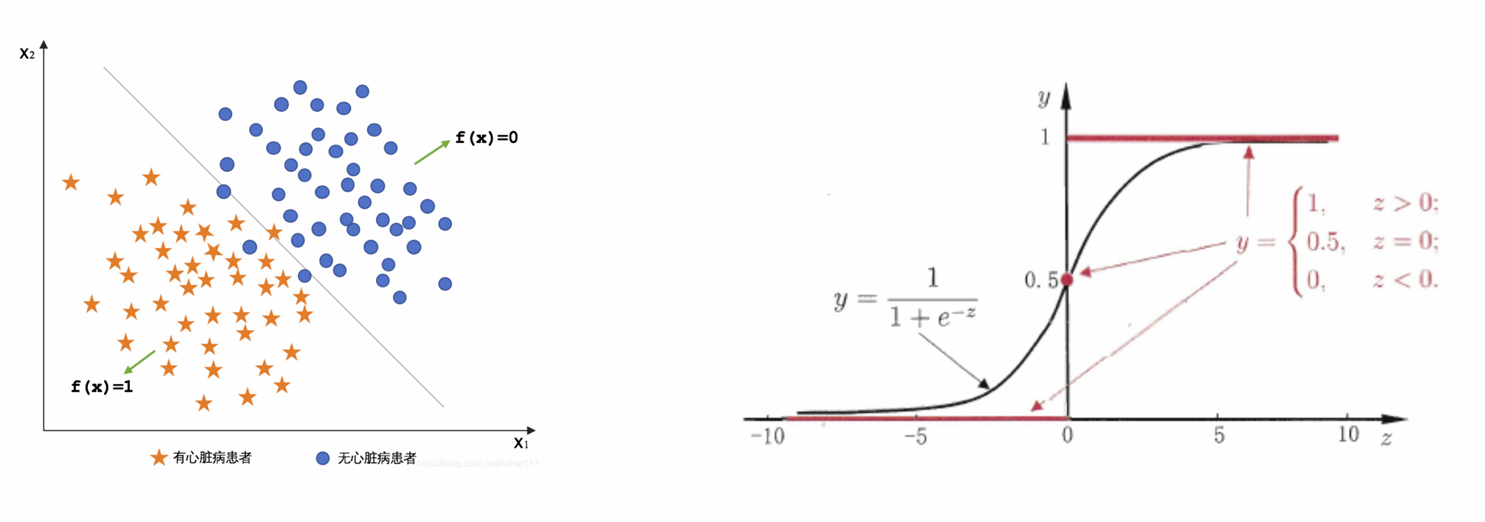二、广义线性模型（GLM）：风险保费预测，根据要提供的保障责任，计算预期总索赔额

1. 直接对纯保费建模
   • tweedie 分布（1,2）
2. 也可以通过两步建模间接近似：纯保费= 索赔次数* 平均索赔金额
   • 索赔次数：泊松分布、负二项分布
   • 平均索赔金额：伽马分布、逆高斯分布

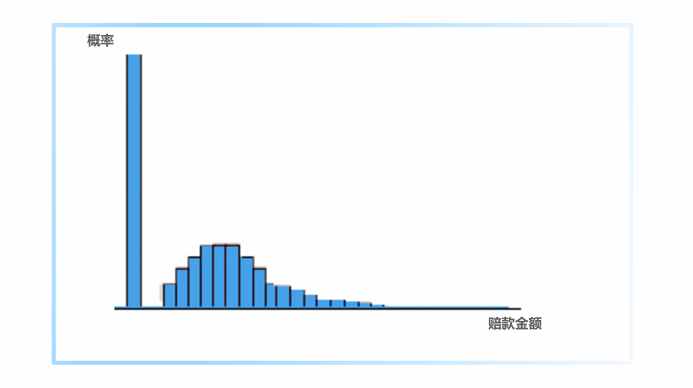广义线性模型

一、 回顾线性回归：它是GLM的一个基本形式，其假设响应变量𝑌的真实值由两部分组成

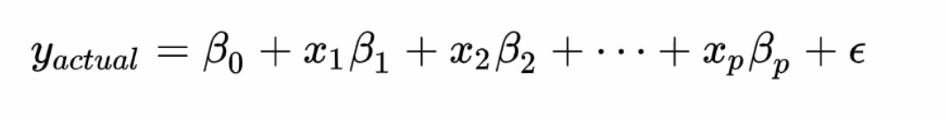
系统组件（system component ）：线性预测器（数值项，可拟合）
误差组件（error component ）：白噪声（高斯随机变量）
线性回归：响应变量𝑌的条件分布为高斯分布
GLM允许误差项的概率分布扩展为指数分布族:伯努利分布
（逻辑回归），泊松分布，gamma分布，复合泊松Gamma
分布，Tweedie分布等

二、广义线性模型的三个关键组件

1. 系统组件：

2. 随机组件

3. 连接函数

隐语模型-密态SSLR/SSGLM

一、广义线性模型参数估计

1. 一阶优化器：SGD参数估计方法

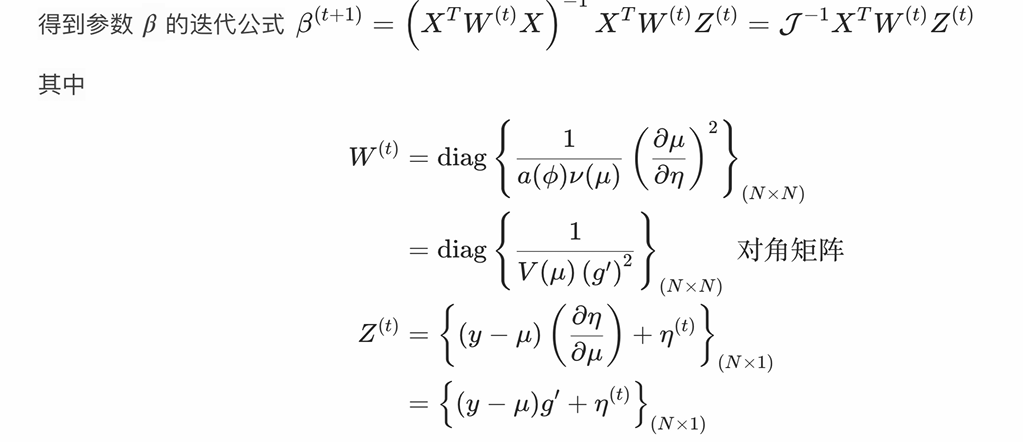
2. 二阶优化器：迭代重加权最小二乘法（IRLS）

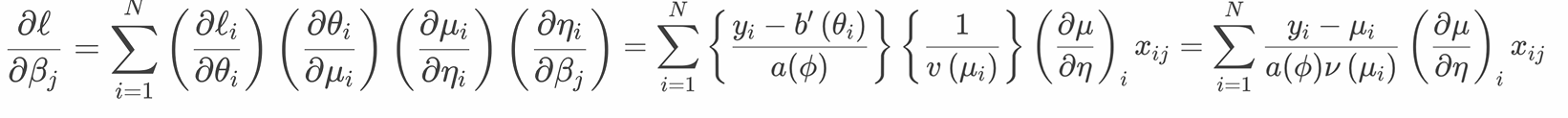
3. 二阶优化器+一阶优化器

二、秘密分享加法

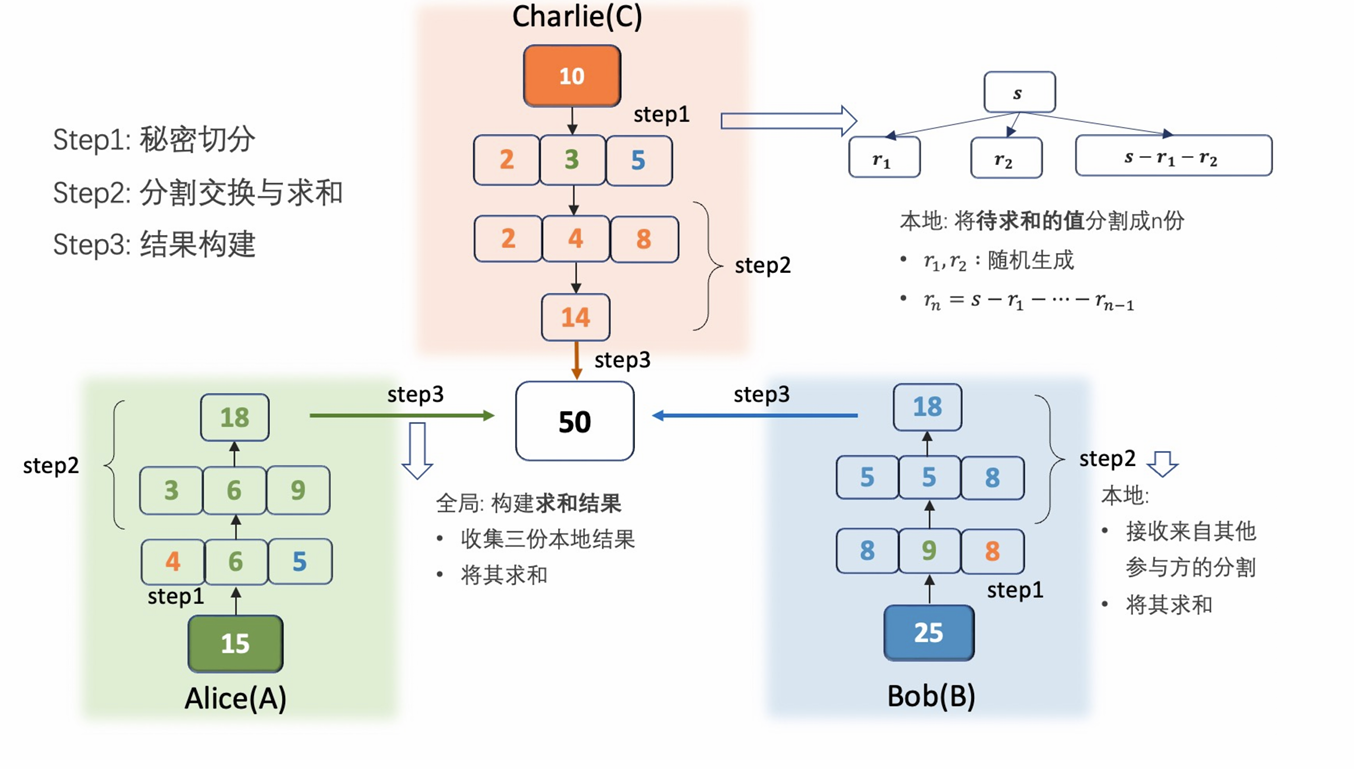三、秘密分享乘法

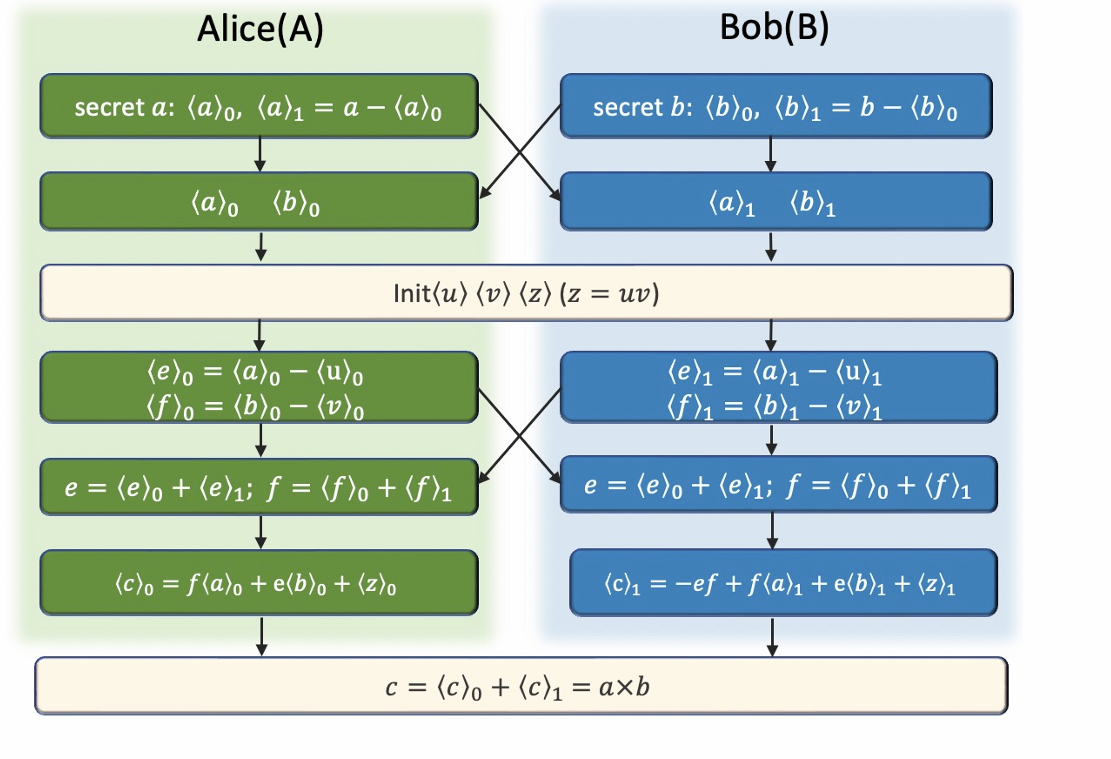应用实现-从理论到隐语应用

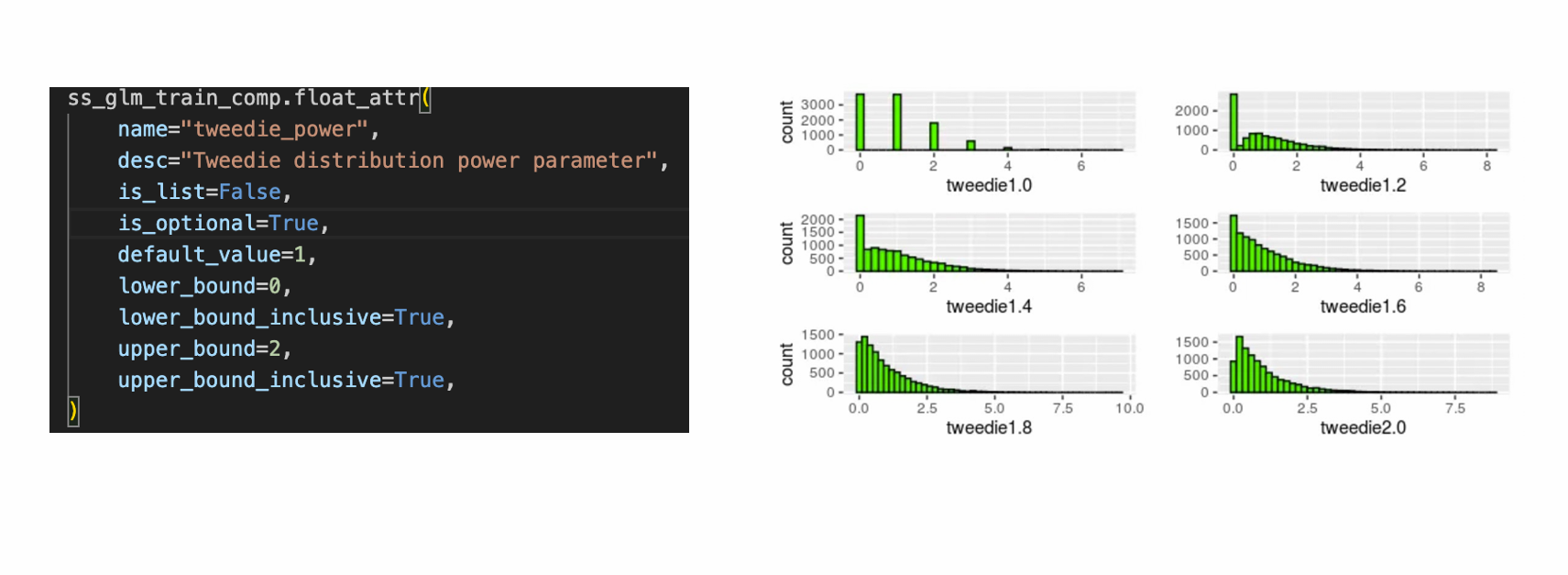
SSGLM参数解析

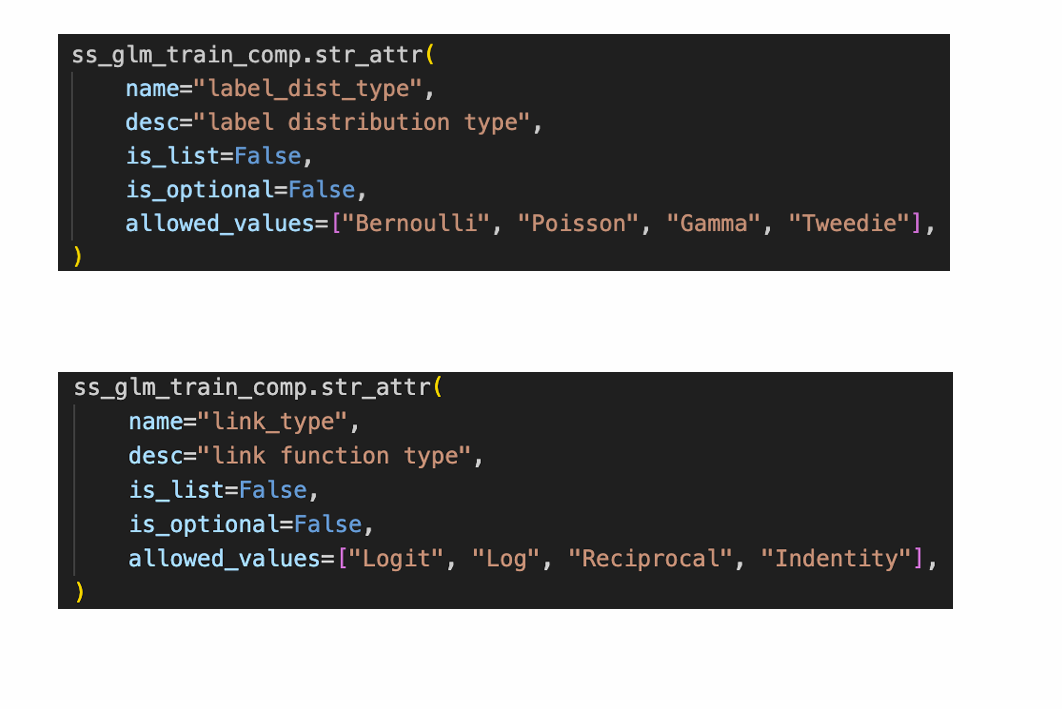
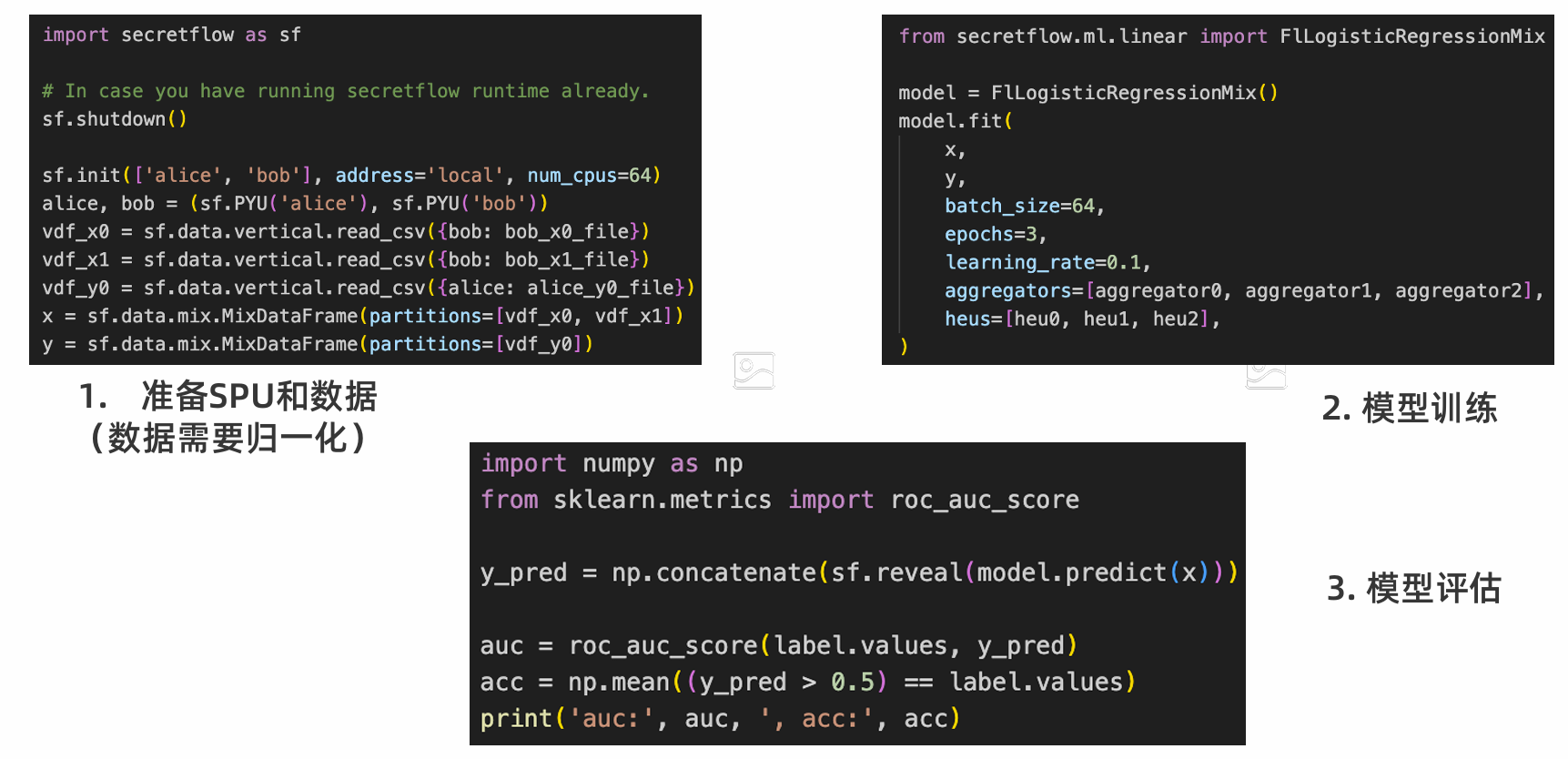
使用SSLR

使用SSGLM

SS-LR / SSGLM 在隐语实现的独特优势

1. 可证安全
2. 不依赖可信第三方
3. 支持多种模型（伯努利分布（逻辑回归），泊松分布，gamma分布，Tweedie分布）
4. 计算高效