马尔可夫奖励(MRP)与决策(MDP)过程

[tianxi_kure]

作用：在不确定环境中做出最优决策

 

随机过程：

其研究对象是随时间演变的随机现象。随机现象在某时刻的状态用St表示。因此P(St+1)=P(St+1|S1,S2,…,St) ，表示已知S1,S2,…,St时下一个时刻状态的概率。

 

马尔可夫过程：

具有马尔可夫性质(某时刻的状态只取决于上一时刻的状态)的随机过程。通常用元组<S,P>来描述。其中P指状态转移矩阵(函数)。

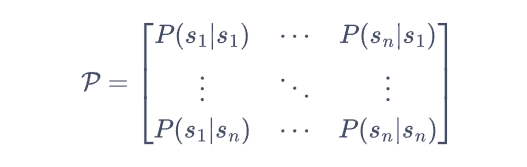
P(Sj|Si)：第i行第j列元素表示从状态Si转移到Sj状态的概率。

需要注意的是：从某个状态出发，到达其他状态的概率和必须为 1，即状态转移矩阵的每一行的和为 1。

 

比如我们以下图的一个随机过程为例子：

 

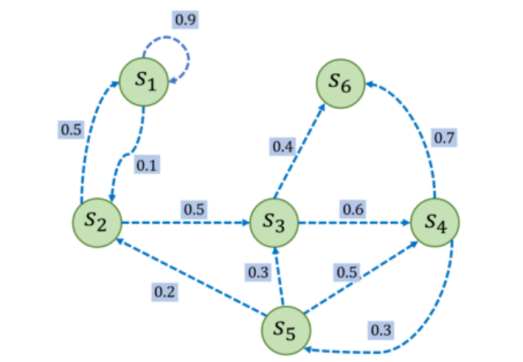
我们就可以写出其P(状态转移矩阵)：

 

马尔可夫奖励过程(MRP)

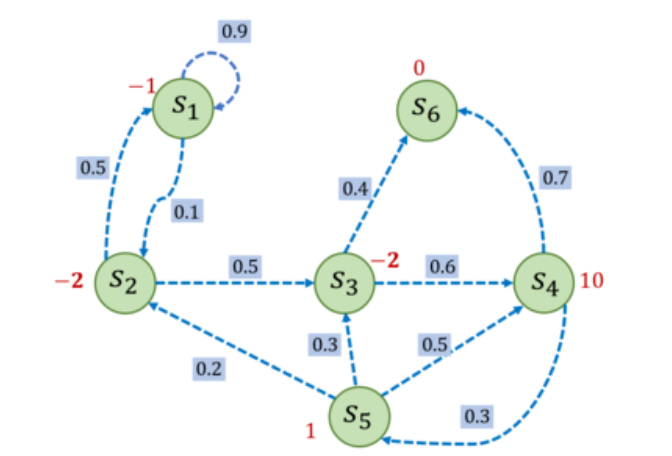
我们在马尔可夫过程过程上

加入奖励函数r和折扣因子γ，

就是MRP

 

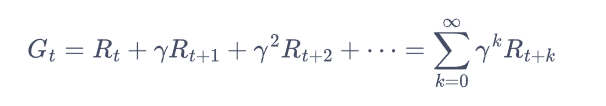
引入γ为的是降低远期收益的影响

 

Gt表示：从第St时刻状态开始，直到终止状态时，所有奖励的衰减之和称为回报

Rt表示：在t时刻时获得的奖励

 

有了上述公式

理论上就可以通过遍历所有路线从而计算出从S1开始，直到S6的最佳回报了

但是这样的话时间复杂度为O(n!)，几乎不适用于复杂项目，而且适用性很低

 

因此我们需要引入价值函数V(s)：直接估算出每个状态的回报

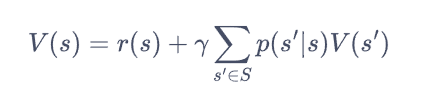
上述式子便是：贝尔曼方程

 

我们将r(s)写成列向量的R，从而有下述解析式：

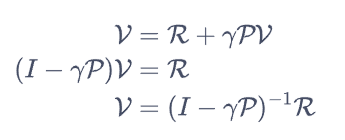
解得各个状态的估算回报，并且将时间复杂度降低为O(n3)。具体代码如下

 

运行后有：

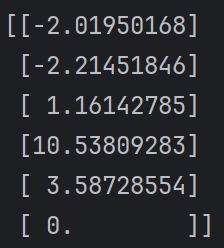
这时我们就可以清晰的观察到每个状态St到达S6时应有的回报

相比回报算法的来说，更为精确

 

上述所讲的均是自发改变的随机过程，若我们引入一个动作变量a

则就是马尔可夫决策过程(MDP)

MRP中的奖励函数r和转移矩阵(函数)P将增加一个变量a，变成：

 

再引入概念 策略：

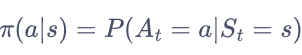
表示在输入状态s情况下采取动作a的概率

 

从而得到的MDP的过程图如图所示：

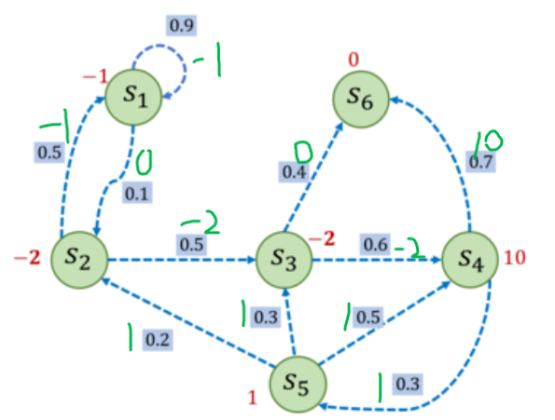
绿色为执行动作得到的奖励 红色为到达状态S得到的奖励 方框为执行状态转移的概率

 

最后引入 状态价值函数

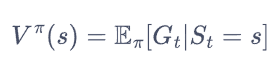
状态s出发遵循策略Π能获得的期望回报

 

引入 动作价值函数

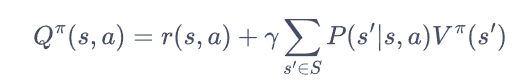
遵循策略Π时，当前状态s执行动作a得到的期望回报

 

从而得到贝尔曼期望方程

 

 

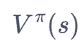
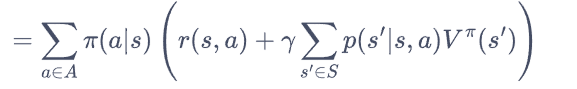
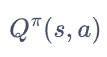
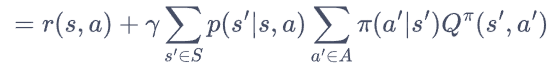
据MDP过程图片 可以给出如下表示

根

 

可以看到此处使用的策略为随机策略

此时，我们若想要计算MDP的每个状态的回报

就需要将将其转化为MRP

方法则是：将策略的动作选择进行边缘化，就可以得到没有动作的 MRP 了。

 

具体如下：

得到有：                                                                       

转移矩阵

 

奖励函数

 

最终输出状态奖励函数：

 

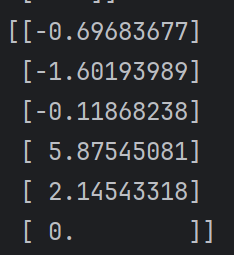
便可以得出动作价值函数：